Требования к оформлению контрольной работы по теории вероятностей и математической статистике

Контрольная работа имеет 10 вариантов (от 0 до 9). Номер варианта определяется по последней цифре номера зачетной книжки.

Работу следует выполнить в отдельной тетради, оставив поля для замечаний рецензента. На обложке тетради должны быть записаны основные данные: специальность, номер учебной группы, фамилия, имя и отчество студента, дисциплина, номер варианта. В конце работы следует указать список использованной литературы (не менее двух источников), поставить дату выполнения работы и подпись.

Решение каждой задачи должно начинаться с ее формулировки и завершаться ответом. Ход решения необходимо описать подробно и аккуратно, сопровождая необходимыми пояснениями и чертежами. Если работа не зачтена и рецензент предлагает ее переделать и прислать для повторной проверки, то доработку следует выполнить в кратчайший срок.

Исправленная работа высылается на повторное рецензирование вместе с предыдущей работой. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех исправлений и дополнений в соответствии с указаниями рецензента.

Студент допускается к экзамену, если контрольная работа зачтена.

Вариант 0

Ребенок играет с четырьмя буквами разрезанной азбуки А, А, М, М. Какова вероятность того, что при случайном разложении букв в ряд он получит слово "МАМА"?
Стрелок трижды стреляет в цель. Вероятность попадания при первом выстреле равна 0,5; при втором – 0,6; при третьем – 0,8. Найти вероятность того, что в мишени будет хотя бы одна пробоина.
В книжном шкафу имеются книги по математике и психологии. На первой полке стоит 20 томов, на второй полке – 24, на третьей – 30, на четвертой – 28. Вероятность того, что взятая наугад книга по математике, составляет: для первой полки – 0,6; для второй – 0,75:для третьей – 0,4; для четвертой – 0,8. Найти вероятность того, что взятая наугад книга с наудачу взятой полки есть книга по математике.
Вероятность того, что автомобиль, взятый напрокат, будет возвращена исправным, равна 0,8. Какова вероятность, что из 4 возвращенных автомобилей 3 окажутся исправными?
В страховом обществе застраховано 5000 автолюбителей. В случае аварии страховое общество выплачивает 750 у.е. Какую минимальную стоимость страхового взноса следует установить, чтобы вероятность того, что страховое общество к концу года окажется в убытке, была не больше 0, 0062, если вероятность автолюбителю попасть в аварию равна 0, 004?
Симметричную монету бросили два раза. Случайная величина (СВ) Х –– число выпавших гербов. Получить ряд распределения, вычислить функцию распределения F(x) и построить ее график.
Вычислить функцию распределения F(x) и построить ее график. Найти математическое ожидание и дисперсию дискретной случайной величины, заданной рядом распределения

x_i	-2	-1	0	1
p_i	0,1	0,3	0,1	0,5

Плотность вероятности случайной величины Х равна

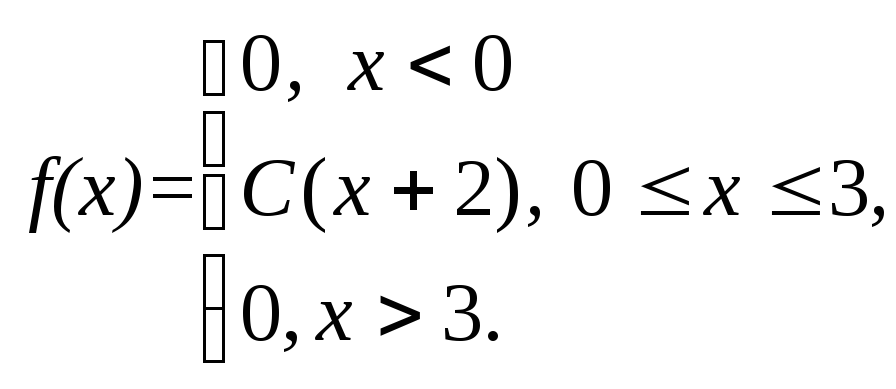
Найти постоянную С, функцию распределения F(x), математическое ожидание и вероятность попадания СВ на отрезок . Построить графики функцийF(x) и

9. По выборке одномерной случайной величины

построить график эмпирической функции распределения ,
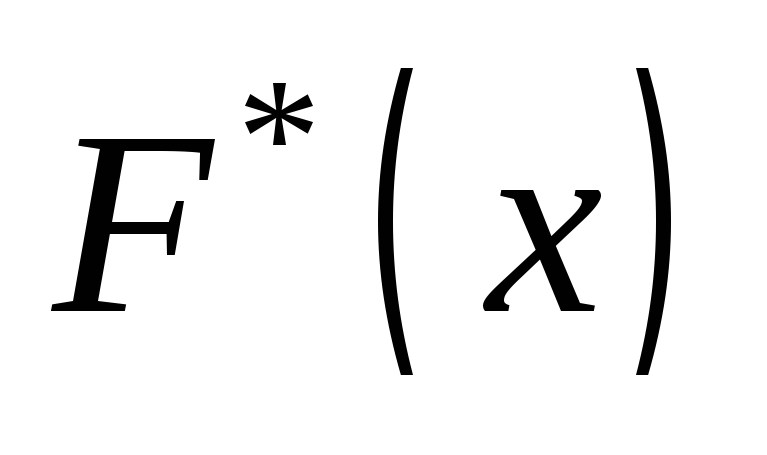построить гистограмму относительных частот равноинтервальным способом,
вычислить точечные оценки математического ожидания и дисперсии,
вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности ,
выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия Пирсона при уровне значимости .

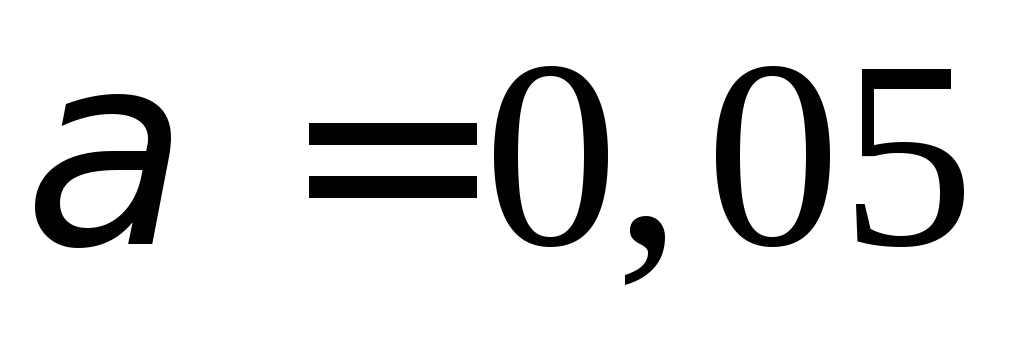Одномерная выборка:

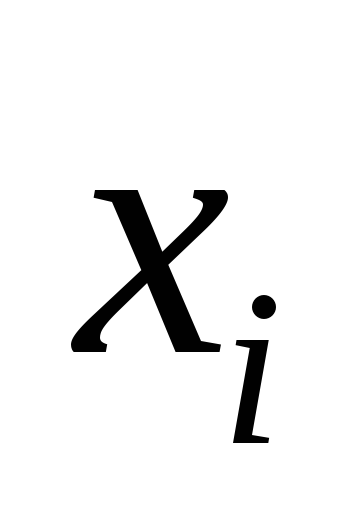
	0,1-0,2	0,2-0,3	0,3-0,4	0,4-0,5	0,5-0,6
	7	22	38	24	9

10. По корреляционной таблице двумерной случайной величины

вычислить выборочный коэффициент корреляции ,
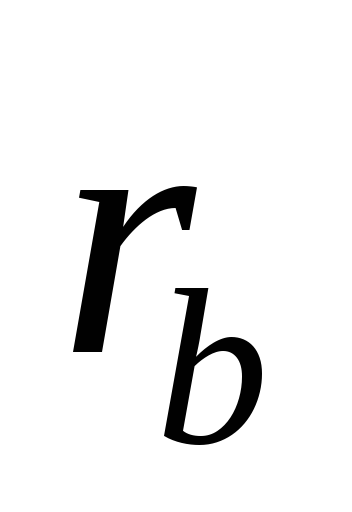проверить нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе 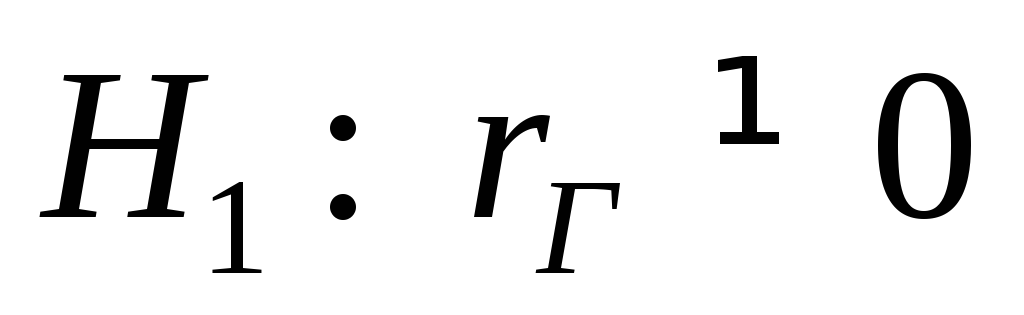при уровне значимости,
найти эмпирическое уравнение прямой лини регрессии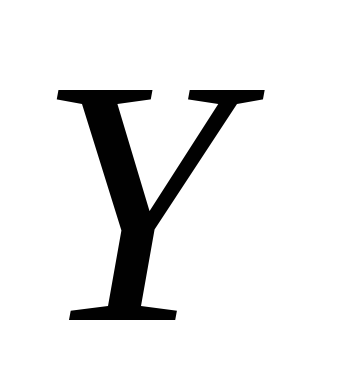на.

Корреляционная таблица:

	5	10	15	20	25	30
100	-	6	4	2	-	2
110	4	2	8	1	5	-
120	-	-	-	10	7	1
130	5	3	8	-	6	7
140	9	5	-	4	-	1

1 / 51 2 3 4 5 > Следующая >>>