
- •Информатики и радиоэлектроники
- •Метрология и измерения Учебно - методическое пособие
- •Минск 1999
- •Содержание
- •1 ПОгрешности средств измерений
- •Задача № 4
- •Решение
- •Задача № 5
- •Решение
- •Задача № 1
- •Контрольные вопросы
- •Решение типовых задач Задача № 1
- •Решение
- •Задача № 2
- •Решение
- •Задача № 3
- •Решение
- •Задачи для самостоятельного решения Задача № 1
- •Задача № 2
- •Задача № 3
- •3 Обработка результатов многократных наблюдений при прямых измерениях
- •Решение типовых задач Задача № 1
- •Решение
- •Продолжение таблицы 2
- •Продолжение таблицы 2
- •Tаблица 3 - Статистика d
- •Задача № 2
- •Решение
- •Задачи для самостоятельного решения Задача № 1
- •Задача №2
- •Задача №3
- •Задача №4
- •Продолжение таблицы 8
- •4 Обработка результатов многократных наблюдений при косвенных измерениях
- •Методические указания
- •Решение типовых задач Задача № 1
- •Решение
- •Задача №2
- •Решение
- •Задачи для самостоятельного решения Задача № 1
- •Задача № 2
- •Задача № 3
- •Задача № 4
- •5 Обработка результатов наблюдений при совокупных и совместных измерениях
- •Решение типовых задач Задача № 1
- •Решение
- •Задача № 2
- •Решение
- •Задачи для самостоятельного решения Задача № 1
- •Задача № 2
- •6 Измерение напряжений
- •Решение типовых задач Задача № 1
- •Решение
- •Задача № 2
- •Решение
- •Задача № 3
- •Решение
- •Задачи для самостоятельного решения Задача № 1
- •Задача № 2
- •Задача № 3
- •Задача № 4
- •7 Измерение частоты, периода, интервалов времени и фазовых сдвигов
- •Решение типовых задач Задача № 1
- •Задача № 2
- •Решение типовых задач Задача № 1
- •Решение
- •Задача № 2
- •Метрология и измерения Учебно - методическое пособие
- •Под общей редакцией с.В. Лялькова
Задача № 3
Определить доверительные границы результирующей погрешности измерения напряжения U=200 мВ при однократном наблюдении с Рд= 0,95. Измерение осуществляется с помощью автоматического потенциометра класса точности 0,5. Изменение температуры вызывает смещение нуля потенциометра на Т= =0,1 % /10С. Нормальные условия эксплуатации потенциометра 202С, потенциометр стоит в помещении, температура которого меняется от 8 до 32С. Нормальные условия для напряжения питания Uн=200 В2 %, а в реальных условиях эксплуатации напряжение может меняться на 10 % Uн. Напряжение наводки в линии связи частотой 50 Гц может достигать 1 мВ.
Решение
1 Основная погрешность аналогового регистратора определяется его классом точности. Погрешность всех электроизмерительных приборов согласно стандарту нормируется с 25 %-м запасом на старение, т.е. фактически погрешность нового прибора составляет не больше, чем 0,8. Следовательно, рег =
=0,80,5=0,4 (%).
2
У потенциометра преобладающей является
погрешность дискретности, обусловленная
конечным числом витков обмотки датчика,
по которым скользит подвижный контакт.
Эта погрешность имеет равномерное
распределение. В этом случае рег
=0,4
(%) можно считать половиной ширины этого
равномерного распределения, и тогда
 %.
%.
3
Погрешность от колебаний напряжения
питания распределена по треугольному
закону с принятыми пределами 10
%. Поэтому максимальное значение этой
погрешности
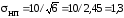 %. Параметры этого распределения:
энтропийный коэффициентk=2,02;
эксцесс =2,4;
=0,645.
%. Параметры этого распределения:
энтропийный коэффициентk=2,02;
эксцесс =2,4;
=0,645.


4 Погрешность наводки распределена арксинусоидально. Энтропийный ко-эффициент k=1,11. Тогда

5
Погрешность смещения нуля потенциометра
при колебании температуры является
аддитивной, а закон ее распределения
можно считать равномерным со средним
значением 20С
и размахом 12С
(так как температура в помещении меняется
от 8 до 32С).
Максимальное значение этой погрешности
при Т=
=0,1
% /10С
составляет
 %,
так какkэ
для равномерного распределения равен
%,
так какkэ
для равномерного распределения равен .
.
6 Суммирование погрешностей сводится к вычислению приведенной погрешности при х = 0, которая складывается из всех аддитивных составляющих, и в конце диапазона, которая складывается из всех составляющих.
При х=0 погрешность будет складываться из трех составляющих:
п=0,24 %, Т=0,07 %, нп=1,30 %.
Однако т =0,07 % меньше нп =1,3 % в 18,5 раз. Так как суммирование под корнем будет производиться над квадратами величин, то ее вклад в результат будет ничтожным. Отсюда ясно, что этой погрешностью можно пренебречь и опустить из дальнейшего рассмотрения. Тогда
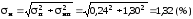 .
.
Для расчета погрешности в конце диапазона к полученному значению н надо добавить погрешность наводки нав.= 0,45 %:
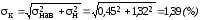 .
.
Для перехода к интервальной оценке в виде доверительного д = t или энтропийного э = k значений необходимо знание не самого закона распределения результирующей погрешности, а лишь его одного числового параметра в виде квантильного множителя t или энтропийного коэффициента k.
Зависимости энтропийного коэффициента k от соотношения суммируемых составляющих и их энтропийных коэффициентов могут быть представлены в виде семейства графиков (график 1 и график 2).
По
оси абсцисс отложены значения
относительного веса дисперсии
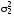 второго из суммируемых распреде-лений
в полной дисперсии
второго из суммируемых распреде-лений
в полной дисперсии ,
по оси ординат – значение энтропийного
коэффициен-таk
образующейся
при этом ком-позиции. Кривая 1 соответствует
композиции двух нормальных рас-
,
по оси ординат – значение энтропийного
коэффициен-таk
образующейся
при этом ком-позиции. Кривая 1 соответствует
композиции двух нормальных рас-
пределений (k = 2,066 для любых значений веса р); кривая 2 – композиции равномерно распределенной и нормально распределенной погрешностей; кри-вая 3 – композиции двух равномерных распределений; кривая 4 –композиции арксинусоидальной и равномерно распределенной погрешностей; кривая 5 –для двух арксинусоидально распределенных погрешностей.
Кривые 1-3 соответствуют сумми-рованию равномерного, треугольного и нормального распределений с дискретным двузначным распре-делением, а кривые 4-6 – суммированию нормального распределения соответственно с арксинусоидальным, равномерным и экспоненциальным.
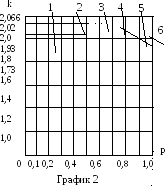
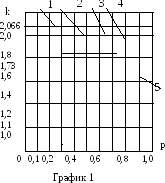
При
х=0 относительный вес нп
в полной дисперсии равен
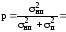
 .
Так как нп
распределена по треугольному закону,
а п
– по равномерному (кривая 2 на графике
2). Отсюда
.
Так как нп
распределена по треугольному закону,
а п
– по равномерному (кривая 2 на графике
2). Отсюда
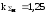 .
.
Тогда при х=0 доверительные границы
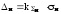 =1,251,3=1,63
(%)
=1,251,3=1,63
(%)
в конце диапазона весовой коэффициент нав. в полной дисперсии равен
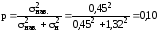
Поскольку нав. распределена по арксинусоидальному, а н – по нормальному законам, воспользуемся кривой 4 на графике 2.
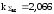 .
.
Тогда
в конце диапазона доверительные границы
 =2,0661,39=
=2,0661,39=
=2,87 (%).
