Задача № 3

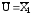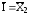Мощность постоянного тока Р измерялась косвенным методом путем многократных измерений напряжения U и тока I c последующим расчетом по формуле P=UI. Воспользовавшись результатами обработки прямых измерений (таблица 10), продолжить обработку результатов косвенного измерения Р_U, оценив его случайную погрешность, записать результат измерения. При обработке принять , В;, мА;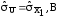;;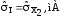; Р_Д= 0,95 - для четных вариантов и Р_Д = 0,99 - для нечетных вариантов.

Задача № 4

Сопротивление R_x определялось путем многократных измерений падения напряжения на нем U_x и падения напряжения U_o на последовательно соединен-ном с ним образцовом резисторе с сопротивлением R_o (кОм) с последующим расчетом по формуле 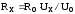. Воспользовавшись результатами обработки прямых измерений (таблица 10), продолжить обработку результатов косвенного измерения R_x и, оценив его случайную погрешность, записать результат измерения. При обработке принять 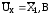;;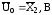;;; 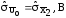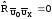Р_Д= 0,95 - для четных вариантов и Р_Д = 0,99 - для нечетных вариантов. Погрешностью резистора R_o пренебречь.

5 Обработка результатов наблюдений при совокупных и совместных измерениях

Рекомендуемая литература: [1, с.211-220], [2, с.167-172], [3, с.6-10, 12].

Методические указания

При изучении темы необходимо особо обратить внимание на следующее:

- отличие cовокупных и совместных измерений от прямых и косвенных;

- примеры совокупных и совместных измерений;

- суть метода наименьших квадратов и использование этого метода при составлении системы нормальных измерений.

Контрольные вопросы

1 Что такое совокупные измерения?

2 Чем совместные измерения отличаются от совокупных?

3 Что собой представляет система исходных уравнений?

4 Что такое невязка уравнений связи?

5 Объясните суть метода наименьших квадратов.

6 Каким образом составляется система нормальных уравнений и какие известны методы ее решения?

Решение типовых задач Задача № 1

Совокупные измерения углов трехгранной призмы выполнены с трехкратным повторением наблюдений. Результаты наблюдений следующие:

₁ = 89^55; ₁ = 45^5; ₁ = 44^57;

₂ = 89^59; ₂ = 45^6; ₂ = 44^55;

₃ = 89^57; ₃ = 45^5; ₃ = 44^58.

Найти с доверительной вероятностью Р_д = 0,95 результаты совокупных измерений углов , , .

Решение

Если найти каждый из углов как среднее арифметическое результатов соответствующих наблюдений, то получим:

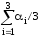₀ == 89^57; ₀ = 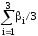= 45^5.33; ₀ = 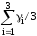= 44^56,67.

Сумма углов треугольника должна удовлетворять условию  +  +  = 180^.

У нас же получилось ₀ + ₀ + ₀ = 179^59.

Это несовпадение - результат погрешностей измерений. Необходимо изменить полученные значения ₀, ₀, и ₀ с тем, чтобы точно известное условие было выполнено.

Примем  = ₀ + _;  = ₀ + _;  = ₀ + _, и будем искать значения поправок _, _, _.

Получаем:

_1 = ₁  ₀ = 2; _1 = ₁ - ₀ = 0.33; _1 = ₁ - ₀ = +0.33;

_2 = ₂  ₀ = +2; _2 = ₂  ₀ = +0.67; _2 = ₂ - ₀ = 1.67;

_3 = ₃  ₀ = 0; _3 = ₃  ₀ = 0.33; _3 = ₃ - ₀ = +1.33.

Уравнение связи имеет вид ₀+_+₀+_+₀+_= 180^.

Следовательно, _ + _ + _ = 180^  179^59 = 1.

Исключим из исходных уравнений , пользуясь соотношением _=1  _

 _, и в каждом уравнении укажем оба неизвестных. Получаем следующую систему исходных уравнений:

A₁  _ + B₁  _ = _1; A₄  _ + B₄  _ = _1;

A₂  _ + B₂  _ = _2; A₅  _ + B₅  _ = _2;

A₃  _ + B₃  _ = _3; A₆  _ + B₆  _ = _3;

A₇  _ + B₇  _ = 1  _1; A₈  _ + B₈  _ = 1  _2;

A₉  _ + B₉  _ = 1  _3,

где

A₁ = 1; B₁ = 0; A₄ = 0; B₄ = 1; A₇ = 1; B₇ = 1;

1  ₁ = +0,67;

A₂ = 1; B₂ = 0; A₅ = 0; B₅ = 1; A₈ = 1; B₈ = 1;

1  ₂ = +2,67;

A₃ = 1; B₃ = 0; A₆ = 0; B₆ = 1; A₉ = 1; B₉ = 1;

1  ₃ =  0,33,

т.е.

1  _ + 0  _ = 2; 0  _ + 1  _ =  0,33;

1  _ + 0  _ = +2; 0  _ + 1  _ = +0,67;

1  _ + 0  _ = 0; 0  _ + 1  _ =  0,33;

1  _ + 1  _ = +0,67; 1  _ + 1  _ = +2,67;

1  _ + 1  _ =  0,33.

Теперь составим систему нормальных уравнений:

A₁₁ = 1 + 1 + 1 + 1 + 1 + 1 = 6; A₁₂ = 1 + 1 + 1 = 3;

A₂₁ = 1 + 1 + 1 = 3; A₂₂ = 1 + 1 + 1 + 1 + 1 + 1 = 6;

C₁ = 2 + 2 +0.67 + 2,67  0,33 = +3;

C₂ = 0,33 + 0,67  0,33 + 0,67 + 2,67  0,33 = +3.

Следовательно, нормальные уравнения примут вид

6  _ + 3  _ = 3;

3  _ + 6  _ = 3.

Вычислим определители Д, и: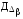

;

;

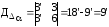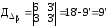
и находим .

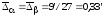Следовательно, и .

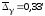Подставляя полученные оценки в исходные уравнения, вычислим невязки:

₁ = 2,33; ₄ = 0,67 ; ₇ = 0;

₂ = -1,67; ₅ = -0,33; ₈ = -2;

₃ = 0,33; ₆ = 0,67; ₉ = 1.

Вычислим оценки с.к.о. результатов совокупных измерений: Д₁₁ =6; Д₂₂ = 6 (алгебраические дополнения элементов определителя Д):

.

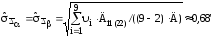Ввиду равноточности исходных уравнений и равенства оценок 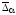,,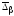, 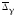можно не делать повторных вычислений, а записать, что.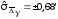

Оценим доверительные границы погрешностей измерения. Для Р_д = 0,95 и t_p = 1,96:

.

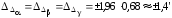Окончательно можно записать результаты измерений:

 = 8957,3  1,4;  = 455,7  1,4;  = 4457  1,4; P_д = 0,95.