РГР / РГР №11 Расчёт прямоугольных и кольцевых пластин. Задача 1, строка 11; строка 6

Задача №1

Для стальной прямоугольной шарнирно опёртой пластины, находящейся под действием распределённой поперечной нагрузки (см. рис. 1.1)

Рис. 1.1.

при числовых значениях размеров по строке № 11 и нагрузки по строке № 6 таблицы 1 требуется:

• определить прогиб и внутренние усилия в пластине и построить их эпюры;

• определить толщину пластины h из условий прочности по энергетической теории и жесткости, приняв условие или (a или b длина меньшей стороны пластины).

• построить эпюры напряжений в точке пластины с координатами .

В расчетах принять:

Под действием заданной нагрузки прогиб пластины также изменяется по одной полуволне синусоиды вдоль координатных линий:

При этом граничные условия шарнирного опирания выполняются точно:

Подставив выражения для прогиба и нагрузки в дифференциальное уравнение изгиба пластины

получим:

Здесь D – жесткость пластины при изгибе, определяемая по формуле:

Определим внутренние усилия в пластине:

Наибольшие значения прогиб и изгибающие моменты имеют в середине пластины , а крутящий момент – в угловых точках. Поперечные силы имеют наибольшие значения в середине сторон.

Определим числовые значения наибольших внутренних усилий.

Характер эпюр прогиба и внутренних усилий показан на рис. 1.2.

Рис. 1.2

Определим толщину пластины h из условия прочности по энергетической теории. Опасными в смысле прочности являются точки 1 и 2. В этих точках изгибающие и крутящий моменты имеют наибольшие значения, а поперечные силы равны нулю.

Выразив наибольшие значения напряжений через М_x, М_y и Н и использовав формулу

получим:

Подставив сюда наибольшие значения внутренних усилий находим

Точка 1

Точка 2

Определим толщину пластины из условия жёсткости, согласно которому наибольший прогиб в середине пластины не должен превышать величину b/200, где b – меньший из размеров сторон пластины.

Учитывая выражение для жесткости, получим

Принимаем с округлением большую толщину h = 0,8 см.

Определим напряжения в точке с координатами . В этой точке все внутренние усилия отличны от нуля и равны половине наибольших. Наибольшие значения напряжений равны:

Эпюры напряжений в данной точке приведены на рис. 1.3.

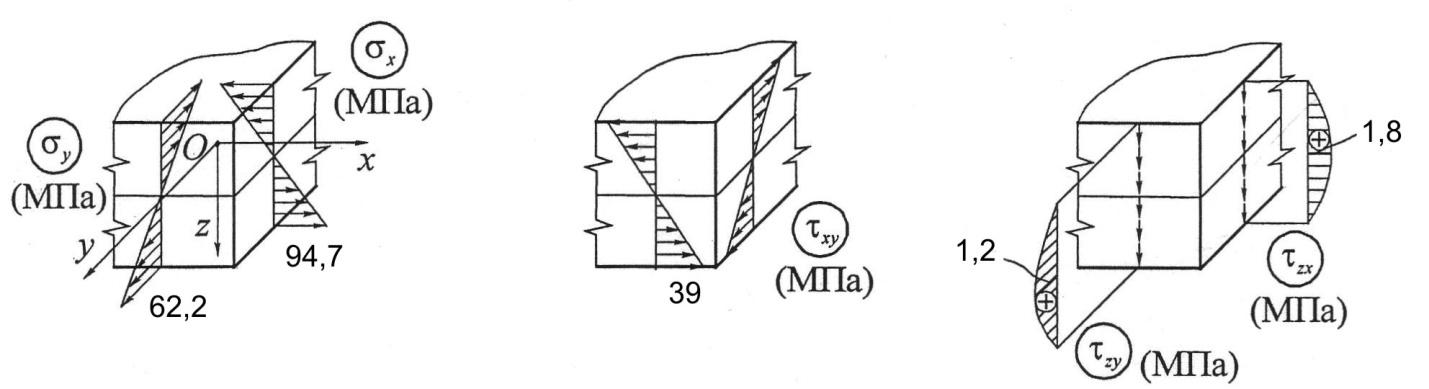
Рис. 1.3

Скачен с http://mgsu.3dn.ru/

7