30. Структура уровней атома водорода.

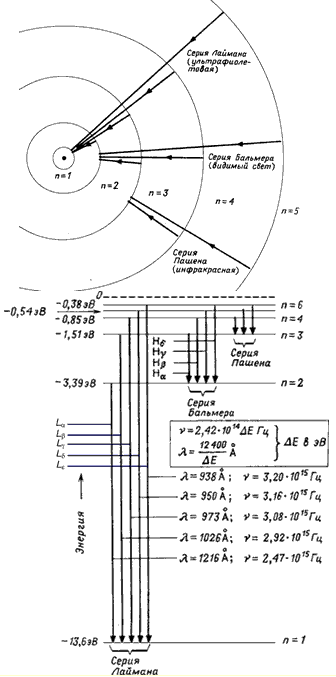
Переходы из состояний n = 2, 3, … ∞ в состояние n = 1 образуют серию Лаймана. Переходы из состояния n = 3, 4, … ∞ в состояние n = 2 – серию Бальмера. Переходы между состояниями с отрицательной энергией (E < 0) приводят к образованию дискретного спектра переходов, в то время как переходы между состояниями с E > 0 и состояниями с E < 0 дают непрерывный спектр переходов.

31. Главное, орбитальное, магнитное, спиновые числа для волновых функций частиц

Квантовые числа

Главное квантовое число n обозначает номер уровня.

n = 1-7 (K-Q). Целое число, характеризует энергию электронов, занимающих данный уровень.

n = 1 - Энергия минимальна

n = 7 - Энергия максимальна, электроны слабо связаны с ядром.

N = 2n2,

где N - максимальное число электронов на уровне, n - номер уровня (главное квантовое число).

Орбитальное = побочное квантовое число l - целое от 0 до n - 1 , определяет форму орбитали.

o l = 0 – s-орбиталь, шарообразная форма

o l = 1 – p-орбиталь, форма объемной восьмерки («гантель»)

o l = 2 – d-орбиталь, более сложная форма

o l = 3 – f-орбиталь, -«-

Электроны с одинаковым l в пределах одного уровня образуют подуровни. Они отличаются энергией связи с ядром. Их число на уровне равно n, но не более 4.

Подуровни обозначают буквами:

o s-подуровень – 1 орбиталь,

o p-подуровень – 3 орбитали,

o d-подуровень – 5 орбиталей,

o f-подуровень – 7 орбиталей.

Элементы, у которых происходит заполнение определенного подуровня, называются соответственно s,p,d,f-элементами.

o s-элементы – элементы главных подгрупп 1 и 2 групп и гелий.

o p-элементы – элементы главных подгрупп 3-8 групп

o d-элементы - элементы вставных декад (переходные элементы)

o f-элементы – лантаноиды и актиноиды.

Магнитное квантовое число m определяет расположение орбитали в пространстве (по осям координат).

m принимает значения от –l до +l, включая 0. Число значений, принимаемых m, определяет число орбиталей на подуровне:

l = 0, m = 0 – 1 s-орбиталь

l = 1, m = -1,0,+1 - 3 p-орбитали

l = 2, m = -2,-1,0, +1,+2 – 5 d-орбиталей

l = 3, m = -3,-2,-1,0,+1,+2,+3 – 7 f-орбиталей

Спиновое квантовое число s характеризует 2 возможных направления вращения электрона вокруг своей оси: s = -½ , s = +½

↑↓ - антипараллельные спины.

32. Принцип Паули. Распределение электронов в атоме по состояниям.

При́нцип Па́ули (принцип запрета) — один из фундаментальных принципов квантовой механики, согласно которому два и более тождественных фермиона (частиц с полуцелым спином) не могут одновременно находиться в одном квантовом состоянии.

Принцип Паули. В атоме не может быть 2 электронов, все 4 квантовых числа которых были бы одинаковыми. Поэтому на каждой орбитали может находиться не более 2 электронов.

33. Понятие о квантовой статистике Бозе-Эйнштейна. Понятие о квантовой статистике Ферми-Дирака.

Квантовая статистика - раздел статистической физики, исследующий системы, которые состоят из огромного числа частиц, подчиняющихся законам квантовой механики.

Идеальный газ из бозонов - бозе-газ - описывается квантовой статистикой Бозе - Эйнштейна*. Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым

Где , ni — количество частиц в состоянии i, gi — вырождение уровня i, εi — энергия состояния i, μ — химпотенциал системы, k — постоянная Больцмана, T — абсолютное значение температуры.

Идеальный газ из фермионов - фермн-газ - описывается квантовой статистикой Ферми - Дирака

Статистика Фе́рми — Дира́ка в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелым спином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние не может занимать более одной частицы); определяет статистическое распределение фермионов по энергетическим уровням системы, находящейся в термодинамическом равновесии;

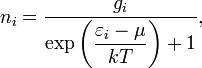
где

ni — среднее число частиц в состоянии i,

Ei — энергия состояния i,

gi — кратность вырождения состояния i (число состояний с энергией ),

μ — химический потенциал (который равен энергии Ферми EF при абсолютном нуле температуры),

k — постоянная Больцмана,

T — абсолютная температура.