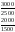- •Министерство образования республики беларусь
- •Технические данные двигателей с полым ротором
- •Технические данные асинхронных двигателей – тахогенераторов с полым ротором серии дг
- •3. Промышленные электрические исполнительные механизмы
- •4. Электромагнитные исполнительные механизмы
- •5. Пневматические и гидравлические
- •6. Сравнительная оценка различных исполнительных механизмов
- •7. Исполнительные механизмы в автоматизированных приводах швейных машин
- •Литература
Технические данные асинхронных двигателей – тахогенераторов с полым ротором серии дг
|
Тип |
UВ.Н, B |
IВ.Н , mA |
f, гц |
Птах, об/мин |
Рн, Вт |
|
ДГ-0,1Т ДТ-0.5А ДГ-0.5Т ДГ-1А ДГ-1Т ДГ-2А ДГ-2Т ДГ-ЗА ДГ-ЗТ |
36 36 36 36 36 36 36 36 36 |
80 100 180 100 120 100 120 80 100 |
400 400 400 400 400 400 400 400 400 |
9000 14000 13000 16000 15000 18000 16000 9000 8000 |
0,07 0,5 0,5 1,0 1,0 2,0 2,0 3,0 3,0 |
2.4. Исполнительные двигатели постоянного тока
Наряду с асинхронными исполнительными двигателями в системах автоматики применяются коллекторные исполнительные двигатели постоянного тока (ИДПТ), которые устойчиво работают при любых частотах вращения, имеют линейные механические характеристики и в большинстве случаев линейные регулировочные характеристики.
По массе и габаритам ИДПТ в 2–3 раза меньше асинхронных микродвигателей. Регулирование частоты вращения ИДПТ осуществляется достаточно просто и экономично.
 Конструкция
коллекторного ИДПТ с независимым
возбуждением показана на рис.7.
Конструкция
коллекторного ИДПТ с независимым
возбуждением показана на рис.7.
Основными элементами двигателя является неподвижный статор (состоящий из корпуса 1, полюсов 2 и обмотки возбуждения 3) и вращающийся якорь (состоящий из цилиндрического магнитопровода с пазами 4, запрессованного на вал 5, обмотки якоря 6, расположенной в пазах магнитопровода, коллектора 7). Ток к якорю двигателя подводится через угольные щетки 8, скользящие по коллектору. Ток, протекающий по обмотке возбуждения, создаёт магнитный поток возбуждения ФВ, пронизывающий обмотку якоря. В результате взаимодействия магнитного потока ФВ с электрическим током, протекающим в обмотке якоря Iя, возникает вращающий момент Мвр, и якорь начинает вращаться с частотой . Величина вращающего момента пропорциональна магнитному потоку возбуждения Фв и току якоря Iя:
Мвр = k·Фв·Iя, (2.12)
где k - постоянный коэффициент, зависящий от конструкции двигателя.
Из коллекторных ИДПТ независимого возбуждения широкое применение получили двигатели серии СЛ, мощностью 7,5 – 230 Вт, частотой вращения 2400 – 5000 об/мин, и моментом на валу 0,014 – 0,92 Нм; серии МИ мощностью 0,1 – 7,0 кВт, частотой вращения 1000 – 3000 об/мин. и моментом на валу 0,32 – 50 Н м. Технические данные некоторых двигателей серии СЛ и МИ приведены в табл.2.5. и 2.6.
Таблица 2.5
|
Тип |
Рн, Вт |
Uн, в |
Iн, a |
Мн, 10-2 Н·м |
Мкр, 10-2 Н·м |
Ip, 10-5 кг/м2 |
nн, об/мин |
|
СЛ-121 СЛ-161 СП-221 СЛ-240 СЛ-261 СЛ-281 СЛ-321 СЛ-361 СЛ-369 СЛ-521 СЛ-569 СЛ-571 СЛ-621 СЛ-661 |
5,0 7,5 13 19 24 26 38 50 55 77 175 95 172 230 |
110 110 110 24 110 24 110 110 110 110 110 24 110 110 |
0,21 0,21 0,35 2,5 0,05 2,4 0,7 0,85 0,9 1,2 2,2 7,0 2,3 2,9 |
1,4 2,1 3,5 4,0 6,5 5,0 12,5 16,0 15 25 47,5 42 70 92,5 |
– – 9,0 – 20 12,5 31,0 40 45 65 92,5 15 125 155 |
– – 1,4 – 2,0 2,0 6,0 7,0 7,0 17 27 27 67,5 93,5 |
4800 4800 3700 4500 3600 5200 3000 3000 3800 3000 3400 2200 2400 2400 |
Таблица 2.6
|
Тип |
UH, В |
Рн, Вт |
Iн, А |
nн, об/мин |
Тип |
UH, B |
Рн, Вт |
Iн, А |
nн, об/мин |
|
МИ 11 |
60 60 110 110 |
120 100 120 100 |
2,86 2,27 1,53 1,22 |
3000 2000 3000 2000 |
МИ41 |
110/220 |
1600 1100 760 |
19,2/9,5 13/6,4 9/4,5 |
2500 1500 1000 |
|
МИ12 |
60 60 110 110 |
200 120 200 120 |
4,57 2,72 2,40 1,46 |
3000 2000 3000 2000 |
МИ42 |
110/220 |
3200 1600 1100 |
36/18 18/9 12,6/6,3 |
2500 1500 1000 |
|
МИ21
|
60 60 110 110 |
250 200 250 200 |
5,6 4,3 3,05 2,33 |
3000 2000 3000 2000 |
МИ51 |
220 |
5000 3200 1600 |
27,2 17,1 8,7 |
2500 1500 1000 |
|
МИ22
|
60/110 |
370 250 120 |
8,2/4,4 5,5/2,9 2,6/1,4 |
3000 2000 1000 |
МИ52 |
220 |
7000 4500 2500 |
37 23,3 13,1 |
2500 1500 1000 |
|
МИ31 |
60/110 |
450 370 200 |
5,6/8,2 4,4/5,0 2,4/4,2 |
1000 |
МИ32 |
110/220 |
760 450 3700 |
8,2/4,1 5,0/2,5 4,2/2,1 |
2500 1500 1000 |
Одним из важнейших требований, предъявляемых к приводам систем автоматического управления, является быстродействие. Это значит, что электропривод должен отрабатывать заданную команду с минимальной задержкой времени. Быстродействие привода в значительной мере определяется быстродействием исполнительного двигателя, которое тем выше, чем меньше момент инерции ротора.
Малоинерционные двигатели постоянного тока выпускают двух видов: с полым немагнитным якорем серии ПДР и дисковым якорем серии ДПО. Эти конструкции характерны только для микродвигателей мощностью до 750 Вт и частично для двигателей малой мощности до 2 кВт.
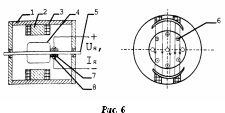
 Двигатель
с полым немагнитным якорем и возбуждением
от постоянных магнитов изображен на
рис.8. Для уменьшения момента инерции
якорь 2 выполнен в виде полого пластмассового
цилиндра, в котором запрессована обмотка
из медного провода или на его поверхности
нанесена обмотка якоря, изготовленная
методом фотолитографии. Полый якорь
вращается в зазоре между внешним 1 и
внутренним 3 статорами. Внутренний
статор выполнен в виде цилиндрического
постоянного магнита и служит для создания
потока возбуждения. Внешний статор,
изготовленный из магнитомягкого
материала, является магнитопроводом.
Двигатель
с полым немагнитным якорем и возбуждением
от постоянных магнитов изображен на
рис.8. Для уменьшения момента инерции
якорь 2 выполнен в виде полого пластмассового
цилиндра, в котором запрессована обмотка
из медного провода или на его поверхности
нанесена обмотка якоря, изготовленная
методом фотолитографии. Полый якорь
вращается в зазоре между внешним 1 и
внутренним 3 статорами. Внутренний
статор выполнен в виде цилиндрического
постоянного магнита и служит для создания
потока возбуждения. Внешний статор,
изготовленный из магнитомягкого
материала, является магнитопроводом.
Напряжение на якорь подаётся через щетки 5 и коллектор 4. Якорь с коллектором насажен на вал б, который вращается в подшипниках 7.
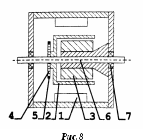
Двигатель постоянного тока с дисковым якорем рис.9, выполняют не с цилиндрическим воздушным зазором, а с плоским.
 Возбуждение
двигателя обеспечивается постоянными
магнитами 1 с полюсными наконечниками
4 из магнитомягкой стали, имеющие форму
кольцевых сегментов. Магнитный поток,
создаваемый постоянными магнитами,
проходит аксиально через два воздушных
зазора, немагнитный дисковый якорь 5 с
печатной обмоткой и замыкается по
кольцам 2 и 3 из магнитомягкой стали,
которые служат ярмом. Роль коллектора
могут играть неизолированные участки
проводников, находящиеся на поверхности
диска, по которым скользят щётки 6.
Возбуждение
двигателя обеспечивается постоянными
магнитами 1 с полюсными наконечниками
4 из магнитомягкой стали, имеющие форму
кольцевых сегментов. Магнитный поток,
создаваемый постоянными магнитами,
проходит аксиально через два воздушных
зазора, немагнитный дисковый якорь 5 с
печатной обмоткой и замыкается по
кольцам 2 и 3 из магнитомягкой стали,
которые служат ярмом. Роль коллектора
могут играть неизолированные участки
проводников, находящиеся на поверхности
диска, по которым скользят щётки 6.
Якорь представляет собой тонкий немагнитный диск 5 с печатной обмоткой. Проводники печатной обмотки располагают радиально по обеим сторонам диска и соединяют через сквозные отверстия в диске.
Основные достоинства двигателей с печатными обмотками: малый момент инерции якоря, хорошая безыскровая коммутация из-за малой индуктивности коммутируемых цепей; хорошее охлаждение обмотки, позволяющее повысить плотность тока.
К недостаткам двигателей этого типа относятся: большой немагнитный зазор, малая механическая прочность якоря, ограниченное число витков обмотки якоря, приводящее к необходимости применять для питания небольшие напряжения.
Технические данные некоторых двигателей серии ПДР и ПДО приведены в табл.2.7.
|
Тип |
Рн, Вт |
Uн, В |
Iн, А |
Тм, мс |
Тэ, мс |
, % |
Мн, Н·м |
Мк, Н·м |
Iр, 10-5 кг·м |
|
ПДР –6 ПДР –3 ДПО –1 ДПО –2 |
60 400 1000 700 |
14 39 48 110 |
7 15 26 7,85 |
9 6 39 18 |
– – 0,12 0,3 |
60 70 67 68 |
0,2 1,35 2,44 2,28 |
0,75 5,4 – – |
2,0 27 137 99 |
Двигатели постоянного тока обладают хорошими регулировочными свойствами, экономичны и др. Наличие скользящего контакта коллектор – щётки ограничивает область их применения.
В настоящее время в связи с развитием сильноточной полупроводниковой электроники появились и начали получать всё более широкое распространение бесконтактные двигатели постоянного тока (БДТП). При замене механического коммутатора коллектор – щётки полупроводниковым коммутатором двигатель постоянного тока становится более надёжным и долговечным, создаёт меньше радиопомех.
В отличие от обычного коллекторного двигателя, БДТП обладает рядом характерных особенностей.
1. Силовая обмотка якоря расположена на статоре и состоит из нескольких катушек, сдвинутых относительно друг друга в пространстве. Ротор выполнен в виде постоянного магнита.
2. Положение магнитного потока ротора по отношению к осям катушек силовой обмотки статора определяется бесконтактным датчиком положения.
3. Бесконтактный (полупроводниковый) коммутатор осуществляет коммутацию катушек силовой обмотки статора по сигналу датчика положения.
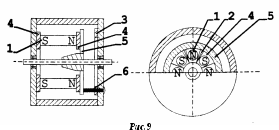
Рассмотрим простейшую конструкцию БДТП (рис.10.).
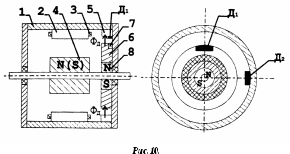 В
корпусе 1 расположены электромагнитные
системы двигателя и датчика положения.
Магнитопровод статора 2 двигателя
выполнен из электротехнической стали.
В его пазах расположена двухфазная
обмотка 3 состоящая из двух обмоток,
сдвинутых в пространстве на 90° . Ротор
4 с одной парой полюсов изготовлен из
постоянного магнита. При подаче
постоянного напряжения на обмотку
статора по ней проходит ток, который
при взаимодействии с магнитным потоком
ротора создает вращающий момент.
В
корпусе 1 расположены электромагнитные
системы двигателя и датчика положения.
Магнитопровод статора 2 двигателя
выполнен из электротехнической стали.
В его пазах расположена двухфазная
обмотка 3 состоящая из двух обмоток,
сдвинутых в пространстве на 90° . Ротор
4 с одной парой полюсов изготовлен из
постоянного магнита. При подаче
постоянного напряжения на обмотку
статора по ней проходит ток, который
при взаимодействии с магнитным потоком
ротора создает вращающий момент.
Роль датчика положения ротора относительно обмоток статора выполняют два магнитоуправляемых диода Д1 и Д2, расположенные на дополнительном кольцевом магнитопроводе 5, и вращающийся ферромагнитный диск 6. Диск имеет немагнитную вставку 7, занимающую половину его толщины на половине окружности. Магнитный поток датчика Фд создается постоянным магнитом 8 с радиальной намагниченностью. Каждый из магнитоуправляемых диодов одну половину оборота вала находится в зоне действия магнитного потока открыт, а вторую – вне зоны действия Фд закрыт.
Работа датчиков и полупроводникового коммутатора К (рис. 11) согласована при расположении Д1 и Д2 по осям обмоток статора 1 и 2 и линии симметрии диска 6 перпендикулярно оси полюсов ротора.
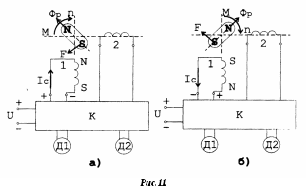 В
положении, изображённом на рис.11а.,
сигнал, управляющий коммутатором,
снимается сдатчика Д1,
и коммутатор подаёт на обмотку 1 напряжение
указанной на рисунке полярности. Когда
сигнал отсутствует, коммутатор К
подаёт на обмотку 1 сигнал противоположной
полярности (рис.11б). Аналогично со сдвигом
на 90° подключается к коммутатору обмотка
2 по сигналам датчика Д2.
При этом изменение коммутатором
полярности напряжения на обмотках
статора осуществляется в
момент
перехода оси потока ротора через ось
данной обмотки статора. Тем самым
обеспечивается изменение направления
тока в обмотке статора и её магнитного
потока при подходе оси полюса ротора
противоположного знака. Следовательно,
сохраняется одно направление вращающего
момента М,
создаваемого силами F,
в пределах одного оборота ротора.
В
положении, изображённом на рис.11а.,
сигнал, управляющий коммутатором,
снимается сдатчика Д1,
и коммутатор подаёт на обмотку 1 напряжение
указанной на рисунке полярности. Когда
сигнал отсутствует, коммутатор К
подаёт на обмотку 1 сигнал противоположной
полярности (рис.11б). Аналогично со сдвигом
на 90° подключается к коммутатору обмотка
2 по сигналам датчика Д2.
При этом изменение коммутатором
полярности напряжения на обмотках
статора осуществляется в
момент
перехода оси потока ротора через ось
данной обмотки статора. Тем самым
обеспечивается изменение направления
тока в обмотке статора и её магнитного
потока при подходе оси полюса ротора
противоположного знака. Следовательно,
сохраняется одно направление вращающего
момента М,
создаваемого силами F,
в пределах одного оборота ротора.
В БДПТ момент взаимодействия каждой обмотки статора, обтекаемой током Ic и потока ротора Фр будет равен:
М = ·Iс·Фр·sin, (2.13)
где – число витков обмотки; = О 180 – угол между потоком Фр и осью обмотки.
Магнитный поток ротора Фp = const. Тогда выражение момента можно преобразовать:
М = См·Ic·sin, (2.14)
где См - коэффициент, зависящий от потока ротора и конструктивных параметров статора.
Согласно полученному выражению момента, при включении напряжения только на одну обмотку статора двигатель не приходит во вращение, если начальное положение ротора соответствует углу , при котором вращающий момент М меньше момента сопротивления на валу.
Наличие двух и более обмоток статора обеспечивает достаточно большой пусковой момент при любом угловом положении ротора. Однако пропорционально числу обмоток увеличивается число чувствительных элементов датчиков положения и транзисторов в коммутаторе. Поэтому не целесообразно делать более трёх-четырёх обмоток.
Технические характеристики некоторых бесколлекторных двигателей постоянного тока с ротором из постоянного магнита приведены в таблице 2.8, а с возбуждением от постоянных магнитов в таблице 2.9.
Таблица 2.8
|
Тип |
Uн, В |
Мн, 10-2, Н·м |
nн, об/мин |
Iн, А |
|
МБ-11-Н2-01 МБ-12-Н2-01 МБ-21-Н2-01 МБ-22-Н2-01 МБ-11-Н1-08 МБ-11-НЗ-01 МБ-12-Ф1-06 МБ-12-Ф1-08 МБ-21-Н1-02 МБ-41-Н1-01 МБ-41-Н1-02 |
27 27 27 27 27 27 14 14 29 27 27 |
0,3.92 0,980 1,96 30,92 1,47 0,2.9 0,3.9 0,7.8 1.1.8 9.8.1 11,8 |
2000 2000 2000 2000 9000 5000 4500 8000 4500 2000 4000 |
0,1 0,19 0,34 0,65 1,1 0,14 0,26 0,95 0,35 1,8 3,1 |
Таблица 2.9
|
Тип |
Рн, Вт |
Uн, В |
Iн, А |
nн, об/мин |
, % |
|
БД-1.2 БД-4.0 БД-6.6 МБ-11-Н1 МБ-12-Н1 МБ-21-Н1 МБ-28-Н1 МБ-31-Н1 |
1,2 4,0 6,5 2,0 4,0 8,0 16,0 32,0 |
20 27 15 27 27 27 27 27 |
0,24 0,3 0,8 0,16 0,31 0,57 1,0 1,82 |
8000 9500 8000 9000 9000 9000 9000 9000 |
25 45 54 46 48 52 59 65 |
Выше рассматривались асинхронные линейные электрические двигатели, преобразующие электрическую энергию в механическую возвратно-поступательного движения без преобразующих устройств. В ряде случаев целесообразно делать линейными и двигатели постоянного тока.
Линейная электрическая машина представляет собой развернутую на плоскости машину вращательного типа, имеющую определённые конструктивные особенности.
На рис.12 показана схема электромагнитной системы линейного бесконтактного двигателя.
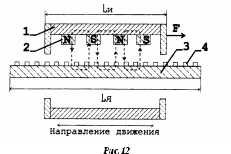 Корпус
индуктора 1 выполнен из ферромагнитного
материала и служит внешним магнитопроводом.
В корпусе расположены постоянные магниты
2, создающие поток возбуждения Ф,
индуктор является подвижной частью
двигателя. Якорь 3 представляет собой
диэлектрическую пластину, на поверхности
которой методом фотолитографии выполнена
печатная схема проводников 4. Якорь
является неподвижной частью двигателя.
Длина якоря Lя
больше длины индуктора на длину хода
индуктора. Проводники якоря объединены
в катушки, оси которых сдвинуты по длине
якоря. Выводы катушек подсоединены к
полупроводниковому коммутатору.
Корпус
индуктора 1 выполнен из ферромагнитного
материала и служит внешним магнитопроводом.
В корпусе расположены постоянные магниты
2, создающие поток возбуждения Ф,
индуктор является подвижной частью
двигателя. Якорь 3 представляет собой
диэлектрическую пластину, на поверхности
которой методом фотолитографии выполнена
печатная схема проводников 4. Якорь
является неподвижной частью двигателя.
Длина якоря Lя
больше длины индуктора на длину хода
индуктора. Проводники якоря объединены
в катушки, оси которых сдвинуты по длине
якоря. Выводы катушек подсоединены к
полупроводниковому коммутатору.
Работа линейного бесконтактного двигателя не отличается от работы рассмотренного ранее вращательного бесконтактного. Отличие состоит в том, что силы электромагнитного взаимодействия тока якоря с полем возбуждения индуктора создают тяговое электромагнитное усилие F в плоском якоре, которое приводит к поступательному перемещению индуктора.
2.5. Передаточная функция двигателя постоянного тока независимого возбуждения.
Переходные процессы в двигателе характеризуются системой уравнений:
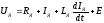 ;
; 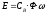 ;
;
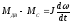 ;
; 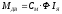 , (2.15)
, (2.15)
где Uя – напряжение на зажимах якорях; Iя – ток в цепи якоря;
Rя,
Lя
– соответственно, сопротивление и
индуктивность цепи двигателя; 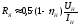 ;
;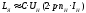 ;С
= 6
8;
;С
= 6
8;
Е - э.д.с. якоря (противо – э.д.с. двигателя);
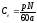 ;
;
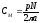 – конструктивные коэффициенты.
– конструктивные коэффициенты.
В результате линеаризации расположением в ряд Тейлора переменных и функций, входящих (2.15), относительно их установившихся значений, обозначенных индексом 0, получим следующие линеаризованные уравнения:
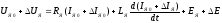 ; (2.16)
; (2.16)
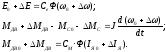
Для установившегося режима двигателя, когда все отклонения переменных равны нулю, уравнения статики: UЯ0 = RЯIЯ0+E0, Е0 = Се · Ф · 0;
МДВ0-МС0 = 0; МДВ = СМ · Ф · IЯ0, (2.17)
Из уравнений (2.17) определяем коэффициенты установившегося режима двигателя:
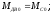
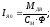
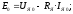
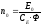 .
.
Коэффициенты Ке = Се·Ф и КМ = СМ·Ф являются постоянными величинами и определяются номинальными данными двигателя:
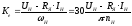 ;
;
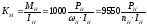 .
.
Уравнение динамики двигателя в отклонениях переменных в соответствии с (2.16) в операторной форме при нулевых начальных условиях запишем в виде:
UЯ(р) = RЯ·IЯ(р) + LЯ·р·IЯ(р) + Е(р);
Е(р) = Kе·(р); (2.18)
МДВ(р) - МС(р) = Jp·(р);
МДВ(р) = КМ·IЯ(р).
Решая совместно эти уравнения, получим:
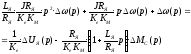 (2.19)
(2.19)
или
(ТЯ·ТМ·р2 + ТМ·р + 1)·(р) = К1·UЯ(р) – К2(1+ТЯр)·МС(р),
где 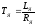 и
и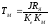 – электромагнитная и электромеханическая
постоянные времени двигателя;
– электромагнитная и электромеханическая
постоянные времени двигателя;
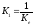 –
коэффициент передачи двигателя;
–
коэффициент передачи двигателя;
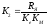 – коэффициент пропорциональности.
– коэффициент пропорциональности.
Если на валу двигателя действует неизменная нагрузка и во всех режимах Мс=const, то МС = 0. При этом уравнение двигателя:
(ТЯ·ТМ·р2 + ТМ·р + 1)·(р) = К1·UЯ(р). (2.20)
Передаточная функция двигателя в этом случае имеет вид:
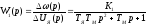 . (2.21)
. (2.21)
Если в качестве выходной координаты двигателя рассматривать угол поворота вала, то, учитывая (р) = р(р), получим передаточную функцию двигателя в виде:
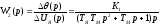 . (2.22)
. (2.22)
Для автоматических систем с маломощными исполнительными двигателями Тм >> Тя, поэтому в расчётах значением ТЯ можно пренебречь и передаточные функции исполнительных двигателей представить в виде:
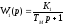 (2.23)
(2.23)
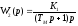 (2.24)
(2.24)
2.6. Тахогенераторы постоянного тока.
Тахогенераторы по принципу действия и конструкции представляют собой электрические коллекторные микромашины постоянного тока с независимым или с самовозбуждением.
Электродвижущая сила якоря машины постоянного тока прямо пропорциональна магнитному потоку возбуждения и частоте вращения якоря:
ЕЯ = К1·n·Ф. (2.25)
Следовательно, при постоянном потоке можно записать:
EЯ = SТ.Г.·n, (2.26)
где SТ.Г. = К · Ф – крутизна тахогенератора при холостом ходе.
При подключении обмотки якоря к выводам прибора или устройства с конечным значением входного сопротивления входное напряжение будет меньше э.д.с. за счёт падения напряжения в цепи якоря.
UЯ = ЕЯ – IЯ · RЯ.Ц., (2.27)
где IЯ - ток якоря; RЯ.Ц. - сопротивление цепи якоря.
Ток
якоря: 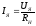 (2.28)
(2.28)
Преобразовав выражение (2.27) с учётом (2.26) и (2.25), получим:
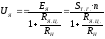 (2.29)
(2.29)
Это уравнение свидетельствует о линейности выходной характеристики тахогенератора постоянного тока. Технические характеристики некоторых типов тахогенераторов постоянного тока приведены в таблице 2.10.
Тахогенераторы работают в переходных режимах, при непрерывном изменении как входного (угол поворота и частота вращения), так и выходного ( Э.д.с. якоря) параметров. Процессы, происходящие в тахогенераторе, описываются дифференциальными уравнениями.
Таблица 2.10
|
Тип |
Э.Д.С.уд, В/(об/с) |
Руд, Вт/(об/с) |
RЯ, Ом |
nmах, об/мин |
UН.В, В |
IН.В, А |
RО.В, Ом |
|
СЛ-121 СЛ-161 СЛ-221 СЛ-261 ТГ-1 ТГ-2 ТГ-3 ТГП-1 ТД-101 ТД-102 ТД-103 ТД-201 ТД-110 ТД-121 ТД-263 |
1,1 1,2 1,5 1,5 0,42 1,27 1,0 0,42 1,4 3,3 6,6 7,7 3,0 0,72 1,08 |
0,0075 0,0085 0,013 0,044 – – – – 0,02 0,028 0,041 0,077 – 0,0045 0,002 |
170 170 117 51 – – – – 330 330 660 780 – – – |
3500 3500 3700 3600 1100 2400 4000 7000 1500 1500 1500 1000 3000 4500 3600 |
110 110 110 110 27 27 27 – 110 110 110 110 – 6 24 |
0,05 0,05 0,05 0,08 0,3 0,3 0,3 – 0,065 0,065 0,06 0,10 – – – |
0,35 0,38 0,7 0,7 3,0 3,0 2,5 0,5 0,5 0,5 0,5 0,8 – – – |
Пренебрегая размагничивающим действием реакции якоря, уравнение переходного процесса тахогенератора имеет вид:
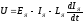 ,
,
где
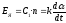 ;LЯ
– индуктивность обмотки якоря;
;LЯ
– индуктивность обмотки якоря;
- угол поворота вала тахогенератора.
Если на выходе тахогенератора включён резистор сопротивлением RH, то ток якоря:
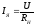
а производная тока:
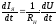 .
.
Решая совместно все эти уравнения, после несложных преобразований получим:
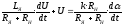 ;
или
;
или
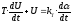 ,
,
где 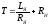 –
постоянная времени якорной цепи;
–
постоянная времени якорной цепи;
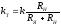 – коэффициент
передачи тахогенератора. Изображение
по Лапласу полученного уравнения имеет
вид:
– коэффициент
передачи тахогенератора. Изображение
по Лапласу полученного уравнения имеет
вид:
Тр·U(p) + U(p) = k·p·(p)
следовательно, передаточная функция тахогенератора:
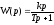 .
.
Таким образом, если входным параметром является угол поворота вала, то тахогенератор представляет собой реальное дифференцирующее звено.
Часто к тахогенератору представляют требования минимальной постоянной времени. Если Т 0, то передаточная функция тахогенератора:
W(P)=kp,
т.е. тахогенератор является идеальным дифференцирующим звеном.
2.7. Шаговые исполнительные двигатели
Шаговые двигатели (ШД) представляют собой многофазные и многополюсные синхронные электрические машины, у которых питание обмоток статора осуществляется импульсным напряжением поочерёдно, с помощью электронного коммутатора. После каждого импульса ротор двигателя поворачивается на определённый угол, называемый шагом. Шаговые двигатели целесообразно применять в тех случаях, когда требуется осуществить прерывистое (стартстопное) движение, а также непрерывное движение, если управляющий сигнал задан в виде серии последовательных импульсов (унитарного кода).
В устройствах автоматики наибольшее применение нашли ШД с числом фаз m3, обмотки которых возбуждаются поочередно или группами импульсами напряжения прямоугольной формы. На рис.13 изображена схема ШД с числом фаз m=6. Если подавать поочередно импульсы напряжения на фазные обмотки 1-2-3-4-5-6, то ротор двигателя будет скачком поворачиваться в положение, при котором его ось совпадает с осью фазной обмотки, находящейся под напряжением, т.е., соответственно, 1-2-3-4-5-6.
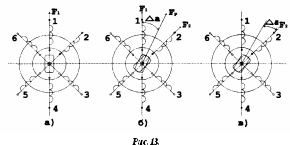 Таким
образом, ротор будет иметь шесть
устойчивых положений, соответствующих
направлению вектора намагничивающей
силы F
фазной обмотки, включённой в данный
момент времени. Шаг двигателя будет при
этом равен =360°/m=360°/6=
60°.
Таким
образом, ротор будет иметь шесть
устойчивых положений, соответствующих
направлению вектора намагничивающей
силы F
фазной обмотки, включённой в данный
момент времени. Шаг двигателя будет при
этом равен =360°/m=360°/6=
60°.
Можно применить и более сложную схему коммутации фазных обмоток, т.е. подавать напряжение одновременно на несколько фазных обмоток. Так, если одновременно подать напряжения на фазы 1 и 2, то ротор повернётся на угол =360°/(2m)=360°/12=30°. Он установится по оси результирующего вектора намагничивающей силы Fp, равного геометрической сумме векторов F1 и F2. При шаге 30° порядок коммутации фазных обмоток рассматриваемого двигателя может быть различным: вариант А - (1) - (1,2) - (2) - (2,3) - (3) ... ; вариант В - (1,2) - (1,2,3) - (2,3) - (2,3,4).
По конструкции ЩД делятся: на магнитоэлектрические, реактивные и индукторные. У магнитоэлектрических ШД ротор выполняется в виде постоянного магнита с одной или несколькими парами полюсов. Статор имеет явно выраженные полюсы, на которые наматываются фазные обмотки.
У реактивного ШД ротор выполняется из магнитомягкого материала, а статор имеет m – фазную сосредоточенную обмотку При малом шаге (15) используют реактивный редукторный ШД с гребенчатыми выступами на статоре. Индукторные ШД по конструкции и принципу работы сходны с редукторными двигателями.
Управление ШД основано на изменении частоты, числа и порядка подачи импульсов постоянного напряжения в фазные обмотки. Изменением частоты импульсов регулируют частоту вращения ШД. Поворот выходного вала ШД на заданный угол осуществляется подачей определённого числа импульсов. Перемена направления вращения выходного вала ШД осуществляется изменением порядка подачи импульсов на фазные обмотки от электронного коммутатора.
Выбирая в качестве исполнительного двигателя шаговый двигатель, необходимо учитывать ряд его особенностей:
1. Положение ротора ШД в статическом режиме устойчивое, т.к. существует синхронизирующий момент, фиксирующий положение ротора по отношению к статору. У двигателей постоянного и переменного тока такого момента нет.
2. ШД может обеспечить широкий диапазон регулирования частоты вращения от максимального до нуля.
3. Движение ротора ШД дискретное с шагом от 1,5° до 36° в зависимости от типа ШД и выбранного числа тактов коммутации фазных обмоток.
4. Скорость изменения частоты управляющих импульсов не должна быть больше определённого для каждого типа ШД значения, называемого частотой приёмистости. Частота приёмистости для серийно выпускаемых ШД может быть в диапазоне от 100 Гц до 2500 Гц.
Технические характеристики некоторых шаговых двигателей приведены в таблице 2.11.
Таблица 2.11
|
Тип |
UН в импульсе, В |
Шаг , град. |
fmax импульсов, Гц |
МН, нагрузки Н·см |
Imax, инерции г·см2 |
Р потребляемая, Вт |
|
ШО-1-0/100 ЩД-16 ЩЦ-1С ЩА-1А ЩДР-111 ЩДР-231 ЩДР-411 ЩДР-521 ЩДА-1 ЩДА-2 РЩД-24 РЩД-20 РЩД-28 РЩЦ-29 ДШ-01 |
14 25 27 25 10 13,5 10 28 28 28 24 27 24 24 27 |
15 15 15 15 15 9 15 9 22,5 22,5 3 3 1 9 5 |
100 400 100 100 1200 1500 1300 1500 400 360 900 800 2000 450 430 |
0,098 0,068 0,098 1,47 0,1 0,4 1,0 1,6 0,39 0,98 0,098 2,45 2,50 0,098 – |
1,96 1,96 1,96 8,0 0,098 0,39 1,0 5,0 2,94 6,85 0,31 5,0 25,0 0,06 18,6 |
2,2 7,0 5,5 6,5 3,0 9,5 10,0 42,0 – – 10 80 300 25 30 |
2.8. Выбор типа исполнительного механизма и редуктора.
Проектирование исполнительной части автоматических систем состоит из следующих этапов: выбор типа исполнительного электродвигателя, предварительного выбора параметров механической передачи, определение мощности исполнительного электродвигателя и уточнение параметров редуктора.
В системах мощностью до 7580 Вт целесообразно применение двухфазных асинхронных двигателей. В более мощных системах применяются электродвигатели постоянного тока. При выборе двигателя необходимо учитывать такой фактор как перегрузочная способность – способность кратковременно развивать максимальный момент. В реальных условиях эксплуатации нагрузка на валу двигателя колеблется в достаточно широких пределах. Для лучшего использования его номинальный момент выбирают из соотношения:
МН = (1,01,8)МС,
где МС– среднее значение нагрузки;
Мн– номинальный крутящий момент двигателя.
Проверка двигателя на нагрузку производится из условия:
Мmax Мн,
где – коэффициент допустимой нагрузки.
Передаточная способность электродвигателей постоянного тока =(34)несколько выше, чем у асинхронных двухфазных электродвигателей<3, поэтому двигатели постоянного тока предпочтительнее в условиях резких изменений момента нагрузки.
При выборе редуктора необходимо обращать внимание на такие характеристики, как КПД, люфт, инерционность.
КПД редуктора влияет на диапазон плавных скоростей электродвигателя. При меньшем КПД диапазон сужается, расширяется зона нечувствительности. К сведению: цилиндрическая зубчатая пара имеет КПД 0,90,94, коническая – 0,880,92, червячная пара 0,50,7, планетарной передачи – 0,80,95. Применение червячных пар не рекомендуется не только из-за низкого КПД, но и из-за возможности заклинивания.
Люфт передачи должен быть минимальным, т.к. может стать причиной автоколебаний. Для уменьшения люфта, когда это необходимо, применяют разрезные шестерни прямозубые и косозубые.
Инерционность редуктора в значительной степени определяется рациональностью распределения передаточных отношений между его ступенями. Замена стальных шестерен пластмассовыми позволяет уменьшить момент инерции на 40-60 %.
При выборе исполнительного двигателя исходными данными служат:
Мс– статический момент нагрузки;
wmax– максимальная угловая скорость нагрузки;
Еmах– максимальное угловое ускорение нагрузки;
Jm– момент инерции исполнительного механизма.
Мощность, развиваемая двигателем, должна быть достаточной, чтобы обеспечить на нагрузке требуемый момент, скорость и ускорение. Поскольку исполнительный электродвигатель связан с нагрузкой через редуктор, то следует привести её к валу двигателя. Приведённый момент инерции нагрузки:
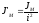 (2.30)
(2.30)
где 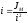 – передаточное отношение редуктора;
– передаточное отношение редуктора;
Jм –момент инерции нагрузки;
– скорость вращения вала двигателя;
н– скорость вращения выходного вала редуктора.
Полный момент инерции равен:
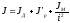 (2.31)
(2.31)
где JД– момент инерции ротора двигателя;
J'P– приведенный момент инерции редуктора.
Динамический момент на валу двигателя:
МД = J·i·max
С учётом КПД редуктора:
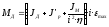 .(2.32)
.(2.32)
Общий момент на валу должен быть равен сумме моментов динамического и статического:
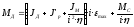 .(2.33)
.(2.33)
Анализ этого выражения показывает, что требуемый от двигателя момент может быть сведён к выбору оптимального для этой цели передаточного отношения. Продифференцируем по iвыражение (2.33) и приравняем результат к нулю:
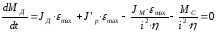 .
.
Отсюда находится оптимальное передаточное отношение:
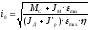 .(2.34)
.(2.34)
Подставив i0в уравнение (2.33) и умножив на, можно получить требуемую мощность двигателя:

Окончательно:
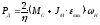 (2.35)
(2.35)
Двигатель выбирается либо мощностью Рдпо выражению (2.35), либо несколько большей. Далее осуществляется проверка:
- определяется оптимальное передаточное отношение;
- проверяется требуемая мощность двигателя по формуле:
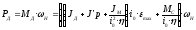 .
.
Двигатель, выбранный таким образом, проверяется по моменту и по скорости, исходя из условий:
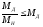 ;
;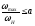 , гдеa
1,2 1,3
, гдеa
1,2 1,3
Изложенная методика рекомендуется при выборе двигателя постоянного тока.
Пример. Выбрать исполнительный двигатель для следящей системы по следующим данным:
МС =14 Н·м; JM = 1,5 кг·м2; Н = 18 об/мин.= 1,88 рад/с; m = 2 рад/с .
Определяем требуемую мощность исполнительного двигателя, задавшись КПД редуктора = 0,8.
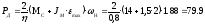 (Вт).
(Вт).
По техническим данным (табл.2.5) выбираем двигатель СЛ–521с параметрами:
Рн = 77 Вт; nН = 3000 об/мин; UH = 110В;
МН =250·10-3 Н·м; Мкр = 650·10-3 Н·м;
м = Мкр/МН = 2,6; JД = 17·10-5 кг·м2.
Определим оптимальное по моменту передаточное число редуктора, приняв J'P=0,2·JД
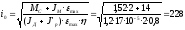 .
.
Вычисляем требуемый максимальный момент
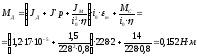
Проверяем перегрузку двигателя по моменту и скорости
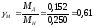 ;
;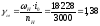 .
.
Двигатель оказался перегружен по скорости, но недогружен по моменту, поэтому нужно уменьшить передаточное число редуктора. Определим передаточное число редуктора, обеспечивающего максимальную скорость нагрузки
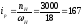 .
.
Пересчитаем максимальный требуемый момент
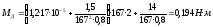
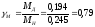 ;
;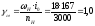 .
.
При выборе двухфазного асинхронного двигателя необходимо руководствоваться следующими соображениями:
- скорость вращения однофазного двигателя определяется частотой напряжения питания, поэтому передаточное отношение находится в соответствии с заданной скоростью вращения нагрузки;
- в ориентировочных расчётах моментом нагрузки можно пренебречь;
- момент инерции редуктора оказывается преобладающим по сравнению с моментом инерции ротора (для двигателей с полым ротором) и нагрузки;
- основное
требование, предъявляемое к электродвигателю
– обеспечение коэффициента динамических
свойств (отношение
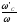 ).
Исходным является уравнение динамики
привода:
).
Исходным является уравнение динамики
привода:
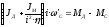 (2.36)
(2.36)
где JД = Jр.Д + J'p– суммарный момент инерции ротора электродвигателя и приведенного момента инерции редуктора;
Мс– приведенный к валу двигателя суммарный
момент нагрузки и редуктора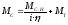 ;
;
Мс.н– статический момент нагрузки;
Мт– момент трения в редукторе;
Мд– вращающий момент двигателя, равный пусковомуМп.
Подставив в формулу (2.36) значение передаточного отношения, получим:
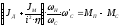 .
.
Это уравнение можно привести к виду:
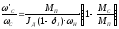 ,(2.37)
,(2.37)
где 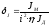 – относительный момент инерции нагрузки.
– относительный момент инерции нагрузки.
Для выбора исполнительного электродвигателя переменного тока необходимо:
1. Вычислить требуемый коэффициент динамических свойств.
2. Определить передаточное отношение редуктора и КПД
3. Вычислить момент инерции редуктора, приведенный к валу двигателя.
4. Определить момент инерции нагрузки, принимая равным нулю момент инерции ротора электродвигателя.
5. Найти приведенный статический момент нагрузки и редуктора.
6. Выбрать двигатель, у которого номинальный вращающий момент не менее Мс.
7. Из числа выбранных взять тот, у которого при проверке по (2.37) коэффициент динамических свойств оказался равным либо большим по сравнению с требуемым.
2.9. Электромагнитные силовые элементы
Исполнительные элементы с электромагнитными силовыми механизмами являются наиболее простыми, надёжными и быстродействующими. Они находят применение для управления стандартными устройствами, для перемещения регулирующих органов на небольшое расстояние, в цифропечатающих устройствах и т.п. Далее для краткости будем их называть "электромагниты".
Если подключить обмотку электромагнита с фиксированным зазором к источнику постоянного тока, то изменение тока в обмотке будет определяться следующим соотношением:
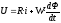 .
(2.38)
.
(2.38)
Умножив (2 38) на i·dtи проинтегрировав за времяt, в течение которого магнитный поток возрастает от0доФ, получим:
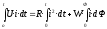 .
(2.39)
.
(2.39)
Левая часть представляет собой электрическую энергию, полученную от источника, первое слагаемое правой части -электрическую энергию, перешедшую в тепловую, и второе –энергию магнитного поля. Пренебрегая потерями в магнитопроводе можно считать всю магнитную энергию сосредоточенной в воздушном зазоре. Величина магнитной энергии определяется:
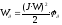 ,
,
где 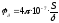 – магнитная проводимость плоско
-параллельного воздушного зазора.
– магнитная проводимость плоско
-параллельного воздушного зазора.
Магнитная энергия затрачивается на совершение работы по перемещению якоря электромагнита под действием тяговой силы Рэ, которая определяется:
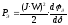 .
(2.40)
.
(2.40)
С учётом значений магнитной проводимости окончательно получим выражение для тяговой силы электромагнита
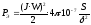 .
(2.41)
.
(2.41)
2. 10. Особенности расчётов электромагнитов переменного тока
Поскольку основным источником питания систем промышленной автоматики является сеть переменного тока, то в связи с этим электромагнитные устройства переменного тока получили достаточно широкое распространение. Из выражения (2.41) видно, что тяговое усилие пропорционально квадрату тока и, следовательно, при изменении направления тока своего знака не меняет.
Для уменьшения потерь на вихревые токи и гистерезис, причиной которых является переменный магнитный поток, магнитопровод выполняют шихтованным из листов электротехнической стали. Для электромагнитов переменного тока характерна вибрация якоря. Причина этого станет ясной из анализа выражения
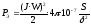 ,
,
здесь i = Jmax · sint;
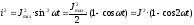 .
.
Подставляя действующее значение тока в исходное выражение, получим:
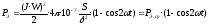 ,
,
Таким образом, тяговая сила электромагнита переменного тока меняется с частотой, вдвое превышающей частоту питания. Это вызывает вибрацию якоря, которая приводит к повышенному износу подвижных частей. Для исключения этого явления электромагнит выполняют двух обмоточным, сдвиг фаз питания обеспечивается подключением к обмоткам индуктивности и ёмкости (рис.14а), либо введением короткозамкнутого витка, который одевается на сердечник (рис.146).
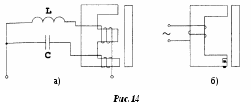 В
результате таких мер в магнитной системе
появляются два пульсирующих магнитных
потока, сдвинутых во времени так, что в
любой момент на якорь действует сила,
отличная от нуля.
В
результате таких мер в магнитной системе
появляются два пульсирующих магнитных
потока, сдвинутых во времени так, что в
любой момент на якорь действует сила,
отличная от нуля.
Тяговая характеристика электромагнита переменного тока зависит от способа его включения и это является ещё одной особенностью этих электромагнитов.
Рассмотрим первый способ, характерный для электромагнитных реле. Обмотка включается последовательно с электрическими устройствами с большим сопротивлением. Ток в такой цепи не зависит от положения якоря, и выражение для тяговой силы электромагнита остаётся в том же виде, что и для электромагнита постоянного тока с плоскими наконечниками:
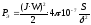 .
.
Второй случай характерен для силовых электромагнитов. В этом случае обмотки включены непосредственно в сеть, напряжение которой можно считать постоянным, независящим от положения якоря. Для этих условий:
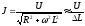 , считаяXL
>> R.
, считаяXL
>> R.
Индуктивность магнита равна:
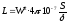 .
.
Отсюда ток в обмотке электромагнита:
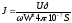 .
.
Подставив значение тока в выражение для тяговой силы получим:
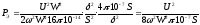 .
.
Из этого выражения видно, что тяговая сила при U = constот величины зазора не зависит.
2.11. Расчет обмоток электромагнита постоянного тока
Укладка обмотки в катушке электромагнита может быть шахматной, шаговой и в навал. В первом случае плотность укладки привода будет наибольшей, в последнем – наименьшей. Плотность укладки определяется величиной коэффициента неплотности КН.
Число витков на единицу площади обмоточного окна находится по формуле:
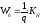 ,
,
где q– площадь поперечного сечения обмоточного провода.
Отсюда число витков в катушке электромагнита:
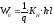 , (2.43)
, (2.43)
где hиl– соответственно, высота и длина обмоточного окна.
Ток питания обмоток определяется известным соотношением:
J=q·j, (2.44)
где j– плотность тока.
Для электромагнитов, работающих в длительном режиме рекомендуемая плотность тока в медном проводе – 3 А/мм2, при повторно-кратковременном режиме 5 А/мм2и при кратковременном 12 А/мм2.
Из (2.43) и (2.44) можно получить выражение для намагничивающей силы
JW = j·KH·h·l. (2.45)
Как видно из этого выражения, размеры обмоточного окна однозначно, с учётом коэффициента неплотности и плотности тока, определяют намагничивающую силу обмотки электромагнита. Электрическое сопротивление обмотки составляет:
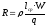 ,
,
где lcр– длина среднего витка,– удельное сопротивление материала обмоточного провода.
Напряжение питания:
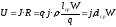 .
.
На завершающей стадии расчёта определяется максимальная температура нагрева обмоток электромагнита. Температура нагрева зависит от соотношения между потребляемой мощностью и поверхностью. При нормальных условиях на 1 Вт потребляемой мощности должно приходиться (814) 10-4м2.
Пример расчёта тягового электромагнита постоянного тока.
Задано: тяговая сила РЭ = 100 н; ход якоря = 10 мм; площадь якорного наконечникаS =4 см2; ток питанияJ = 2А.
1. В соответствии с формулой (2.41) число витков обмотки катушки электромагнита
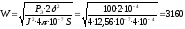 .
.
2. Найдём диаметр обмоточного провода при условии длительного режима работы ( j = 3 А/мм2)
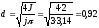 .
.
Выбираем из ряда стандартных диаметров d = 0,92.
3. Определим размеры катушки электромагнита, приняв КН = 0,7, для этого:
а) найдём площадь обмоточного окна
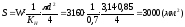 ,
,
б) выберем следующие размеры обмоточного окна: h =30 мм,l = 100 мм,
отсюда размеры катушки: d = 24 мм,D = 84 мм,l = 74 мм.
4. Найдём длину lи сопротивление обмоточного провода:
длина среднего витка составляет:
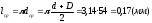 ,
,
отсюда
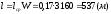 ,
,
сопротивление провода
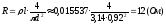 .
.
5. Вычислим напряжение питания электромагнита:
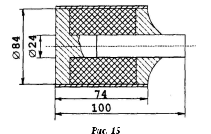
U = J·R = 2 12 = 24 (B).
Электромагнит, соответствующий расчётам, изображён на рис.15.
 Технические
данные некоторых электромагнитов
постоянного и переменного тока приведены,
соответственно, в табл.2.12 и 2.13.
Технические
данные некоторых электромагнитов
постоянного и переменного тока приведены,
соответственно, в табл.2.12 и 2.13.
Таблица 2.12
|
Тип |
ПВ, % |
Рт, Н |
l, мм |
РН, Вт |
m, кг |
tВТ, сек |
tОТП, сек |
|
МП 100 МП200 МП300 КМП2 КМП6 ВМ12 ВМ14 ВМ16 |
25 25 25 25 40 40 40 25 |
250 1000 2150 415 720 65 250 800 |
2 3 4 40 120 40 80 120 |
140 290 510 350 950 210 405 1200 |
– – – – 23,5 1,5 7 3 |
0,12 0,25 0,4 0,4 0,4 0,8 1,6 23,5 |
0,1 0,2 0,35 0,1 0,1 0,2 0,6 1,0 |
Таблица 2.13
|
Тип |
ПВ, % |
МТ, н·м |
МЯ. н·м |
Я, град |
РВКЛ, В·А |
tВТ, сек |
tОТП, сек |
|
КМТЗА КМТ4А КМТ6А КМТ7А МО-100Б МО-200Б МО-300Б |
– – – – 40 40 40 |
350 700 1150 1400 550 4000 10000 |
125 240 460 520 50 360 920 |
50 50 60 80 7,5 5,5 5,5 |
19000 38000 85000 11000 2100 6800 17500 |
0,08 0,14 0,25 0,35 0,3 0,05 0,08 |
0,06 0,08 0,12 0,14 0,02 0,04 0,06 |
2.12. Электромагнитные муфты
В современной технике в различного рода системах автоматического управления используются электромагнитные муфты. Широкая область применения муфт привела к большому разнообразию их видов и конструкций. По характеру связи между входными и выходными элементами муфты можно разбить на следующие группы:
с механической связью (фрикционные) – с электромагнитным и магнитоэлектрическим управлением;
с электромеханической связью (ферропорошковые) – электромагнитные и магнитоэлектрические;
со связью через поле (индукционные, гистерезисные, конденсаторные).
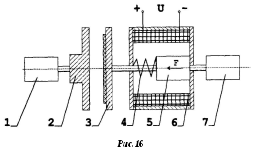 На
рис.16 изображена однодисковая фрикционная
муфта с электромагнитным управлением.
Двигатель привода 1 непрерывно вращает
ведущий вал с диском 2. При вымоченном
состоянии движение на ведомый диск 3 не
передаётся, так как якорь 5 электромагнита
за счёт возвратной пружины 4 находится
в правом положении и межу дисками 2 и 3
существует воздушный зазор. При включении
муфты ток, протекающий по обмотке
электромагнита 6, создаёт магнитное
поле и электромагнитную силуF, втягивающую якорь внутрь обмотки.
Ведомый диск с валом прижимается к
ведущему диску и начинает вращаться,
передавая движение на объект управления
7.
На
рис.16 изображена однодисковая фрикционная
муфта с электромагнитным управлением.
Двигатель привода 1 непрерывно вращает
ведущий вал с диском 2. При вымоченном
состоянии движение на ведомый диск 3 не
передаётся, так как якорь 5 электромагнита
за счёт возвратной пружины 4 находится
в правом положении и межу дисками 2 и 3
существует воздушный зазор. При включении
муфты ток, протекающий по обмотке
электромагнита 6, создаёт магнитное
поле и электромагнитную силуF, втягивающую якорь внутрь обмотки.
Ведомый диск с валом прижимается к
ведущему диску и начинает вращаться,
передавая движение на объект управления
7.
Однодисковая муфта проста по устройству, но малоэффективна и практически нерегулируема по крутящему моменту. Этот недостаток в значительно степени снижен в многодисковых муфтах.
Крутящий момент, передаваемый муфтой вычисляется по формуле:
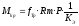 (2.41)
(2.41)
где fTp– коэффициент трения;
R– средний радиус поверхности трения;
m– число пар поверхностей трения;
Р– сила притяжения якоря муфты;
КЭ– коэффициент запаса по крутящему моменту.
Сила притяжения определяется из соотношения:
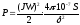 ,
(2.42)
,
(2.42)
где J– ток в обмотке управления;
W– число витков обмотки управления;
S– сечение магнитопровода;
– величина зазора.
Переходной процесс при включении муфты можно разбить на три этапа. Первый этап начинается с момента включения муфты и заканчивается достижением якорем положения, при котором зазор между дисками оказывается равным нулю. Этот этап описывается следующей системой уравнений:
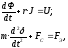 (2.43)
(2.43)
где U– напряжение питания;
r– сопротивление обмотки управления;
m– масса подвижных частей;
Fc– сопротивление движению диска;
FЭ– тяговая сила.
Второй этап начинается с момента соприкосновения поверхностей трения и заканчивается полным сцеплением. В течение этого этапа поверхности трения проскальзывают, а скорость ведущего вала уменьшается до тех пор, пока не сравняется со скоростью ведомого. Система уравнений, описывающих этот этап:
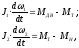 (2.44)
(2.44)
здесь J1 иJ2– моменты инерции, соответственно, ведущей и ведомой частей;
Мдв– момент развиваемый двигателем;
Мт-момент трения;
МН- момент нагрузки;
1,2– скорости вращения ведущей и ведомой частей.
Третий этап начинается после полного сцепления муфты и заканчивается разгоном всех вращающихся частей до номинальной скорости вращения. Этот этап описывается уравнением:
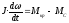 ,
,
где J– полный момент инерции вращающихся частей;
Мкр– крутящий момент;
Мс- момент сопротивления.
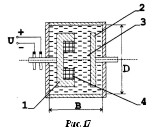 Муфта
с электромеханической связью
(ферропорошковая) изображена на рис.17.
Пространство между полумуфтами 1 и 2
заполнено ферромагнитной средой 3,
состоящей из смеси кремнистого железа
и смазывающего вещества (тальк, графит),
улучшающего проскальзывание полумуфт
при холостом ходе. При подаче тока в
обмотку 4 ведущей полумуфты 1 возникающее
магнитное поле намагничивает отдельные
частички железа, которые слипаются
между собой, и вязкость среды 3
увеличивается. Ведомая полумуфта
начинает вращаться. По мере увеличения
тока в обмотке увеличивается сила
вязкого трения и значение момента
передаваемого на ведомый диск.
Муфта
с электромеханической связью
(ферропорошковая) изображена на рис.17.
Пространство между полумуфтами 1 и 2
заполнено ферромагнитной средой 3,
состоящей из смеси кремнистого железа
и смазывающего вещества (тальк, графит),
улучшающего проскальзывание полумуфт
при холостом ходе. При подаче тока в
обмотку 4 ведущей полумуфты 1 возникающее
магнитное поле намагничивает отдельные
частички железа, которые слипаются
между собой, и вязкость среды 3
увеличивается. Ведомая полумуфта
начинает вращаться. По мере увеличения
тока в обмотке увеличивается сила
вязкого трения и значение момента
передаваемого на ведомый диск.
Таким образом, фрикционные муфты с вязким трением являются управляемыми, позволяющими плавно регулировать передаваемый вращающий момент, а следовательно и частоту вращения ведомого вала.
Крутящий момент, развиваемый муфтой, определяется:
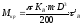 (2.45)
(2.45)
здесь
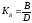 – отношение ширины сцепляющего слоя к
среднему диаметру этого слоя;
– отношение ширины сцепляющего слоя к
среднему диаметру этого слоя;
'В = Кр·В– удельная сила сцепления, в которой принимаютКр=0,70,8;
В = (0,20,4) 105;
m–масса подвижных частей.
Величина·Вявляется исходной при расчёте обмоток управления и параметров магнитной цепи.
Динамические свойства муфты находятся из анализа дифференциальных уравнений электрической цепи и моментов:
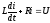 ,
(2.46)
,
(2.46)
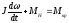 ,
(2.47)
,
(2.47)
где L– индуктивность обмотки управления;
R– активное сопротивление обмотки;
Мн = z · – момент нагрузки, приведённый к ведомому валу;
z – коэффициент вязкого трения;
Мкр= с · i– крутящий момент.
Уравнение (2.47) может быть записано в виде:
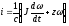 ,
,
подставив полученное таким образом значение iв (2.46), получаем уравнение нагруженной муфты:
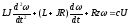 ,
(2.48)
,
(2.48)
и ненагруженной:
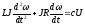 (2.49)
(2.49)
Разделив уравнение (2.48) нагруженной муфты на Rzи подставив:
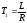 – электрическая постоянная времени;
– электрическая постоянная времени;
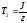 – механическая постоянная времени;
– механическая постоянная времени;
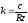 – коэффициент передачи,
– коэффициент передачи,
придём к виду:
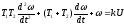 .
.
Отсюда передаточная функция нагруженной муфты:
 .
(2.50)
.
(2.50)
Разделив уравнение ненагруженной муфты на JRпосле соответствующей подстановки, получим:
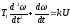 ,
, 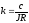 .
.
Отсюда передаточная функция ненагруженной муфты:
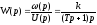 .
(2.51)
.
(2.51)
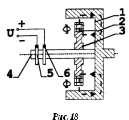 Муфта
со связью через поле (асинхронная
индукционная) изображена на рис.18.
Ведущий вал 4 вращает индуктор, состоящий
из магнитопровода 3 и катушки возбуждения
2. К индуктору через щётки 6 и контактные
кольца 5 подводится во время работы
постоянное напряжение. Возникающий
магнитный поток замыкается через
воздушный зазор и якорь 1. В результате
взаимодействия токов, возникающих в
якоре при вращении индуктора, и
создаваемого его обмоткой 2 магнитного
потока, возникает вращающий момент.
Якорь начинает вращаться вслед за
индуктором и вращать ведомый вал.
Муфта
со связью через поле (асинхронная
индукционная) изображена на рис.18.
Ведущий вал 4 вращает индуктор, состоящий
из магнитопровода 3 и катушки возбуждения
2. К индуктору через щётки 6 и контактные
кольца 5 подводится во время работы
постоянное напряжение. Возникающий
магнитный поток замыкается через
воздушный зазор и якорь 1. В результате
взаимодействия токов, возникающих в
якоре при вращении индуктора, и
создаваемого его обмоткой 2 магнитного
потока, возникает вращающий момент.
Якорь начинает вращаться вслед за
индуктором и вращать ведомый вал.
По принципу действия этой муфты необходимо, чтобы якорь вращался несколько медленнее, чем индуктор, так как в противном случае в якоре не будут индуцироваться токи и исчезнет вращающий момент.
Технические данные электромагнитных фрикционных муфт (МЭС), порошковых (МПБ), гистерезисных (НГБ), торможения (МЭТ) приведены в таблице 2.14.
Таблица 2.14
|
Тип |
U, В |
MН, Н·м |
nН, об/мин |
Мтр, Н·м |
Рн, Вт |
tвк=tотк, мс |
Rобм, Ом |
|
МЭТ 0,1/27 МЭС 0,1/27 МЭТ 0,1/110 МЭС 0,1/110 МЭТ 0,4/27 МЭС 0,4/27 МЭТ 0,4/110 МЭС 0,4/110 МЭТ 1,0/27 МЭС 1,0/27 МЭТ 1,0/110 МЭС 1,0/110 |
27 27 110 110 27 27 110 110 27 27 110 110 |
0,1 0,1 0,1 0,1 0,4 0,4 0,4 0,4 1,0 1,0 1,0 1,0 |
1000 1000 1000 1000 1000 1000 1000 1000 500 500 500 500 |
– 0,003 – 0,003 – 0,01 – 0,01 – 0,02 – 0,02 |
5 5 5 5 7 7 7 7 10 10 10 10 |
40 40 40 40 60 60 60 60 150 150 150 150 |
170 170 2400 2400 100 100 1700 1700 70 70 1200 1200 |
|
МПБ-0,63-2 МПБ-1,6-2 МПБ-4-2 МПБ-10-2 МПБ-25-2 МПБ-40-2 МПБ-63-2 |
24 24 24 24 24 24 24 |
0,06 0,16 0,35 0,98 2,45 3,92 5,20 |
2000 2000 2000 2000 2000 2000 2000 |
– – – – – – – |
12 25 60 100 120 150 180 |
– – – – – – – |
170 192 144 115 82 68 60,5 |
|
МГБ-1,6-3 МГБ-1,6-12 МГБ-2,5-3 МГБ-2,5-12 МГБ-4-3 МГБ-10-6 |
24 24 24 24 24 24 |
0,16 0,16 0,25 0,25 0,4 1,0 |
300 12000 3000 12000 3000 6000 |
– – – – – – |
30 30 40 40 60 90 |
0,74 0,54 0,85 0,66 0,75 1,1 |
18 31,6 14,4 25,3 23 14,4 |