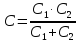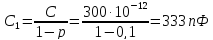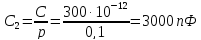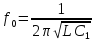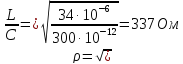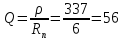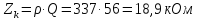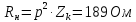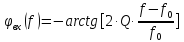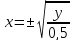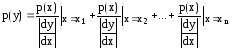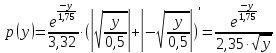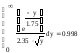Решение

1. При неполном включении нагрузки в цепь контура справедливы следующие выражения:

	(6.1)
	(6.2)

Отсюда найдем емкость конденсаторов:

	(6.3)
	(6.4)

2. Частота резонанса резонансного контура рассчитывается по следующей формуле:

(6.5)

Тогда индуктивность катушки будет равна:

3. Характеристическое сопротивление контура вычисляется по следующей формуле:

(6.6)

4. Добротность контура вычисляется по следующей формуле:

(6.7)

5. Активное сопротивление контура на резонансной частоте определяется следующим выражением:

(6.8)

6. Рассчитаем сопротивление нагрузки для согласования:

(6.9)

7. Величина напряжения на колебательном контуре на уровне f_0.707 равна:

(6.10)

8. На рисунке 9 приведены АЧХ и ФЧХ фильтра.

АЧХ сигнала:

(6.11)

ФЧХ сигнала:

(6.12)

Полоса пропускания на уровне 0,707: 8,9 кГц.

Добротность: .

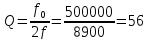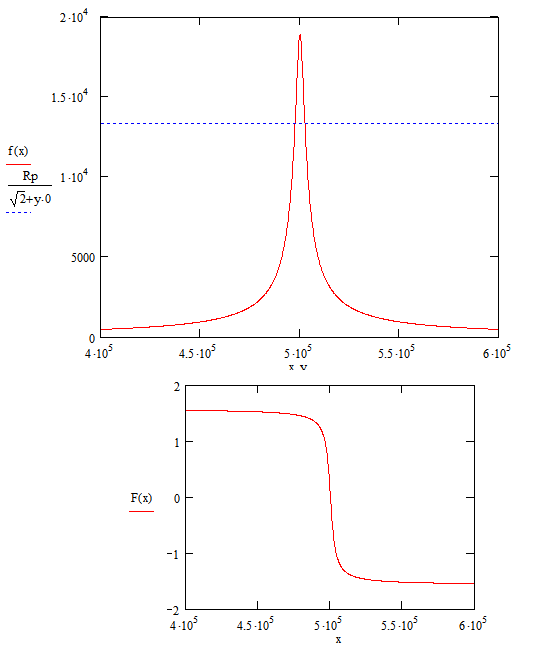
Рисунок 6.2 – АЧХ и ФЧХ фильтпа

ЗАДАЧА 7. На вход безынерционного четырехполюсника с функциональной характеристикой 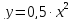воздействует стационарный нормальный процесс, плотность вероятности которого

.

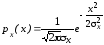
Где _х²= .

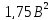Необходимо:

1. построить плотность вероятности p_x(x) и функциональную характеристику f(x);

2. найти плотность вероятности на выходе четырехполюсника p_y(y). Проверить правильность найденного решения по условию нормировки:

.

Построить p_y(y).

3. Рассчитать математическое ожидание и дисперсию выходного сигнала.

Решение

1. Функциональная характеристика f(x) представлена на рисунке 7.1.

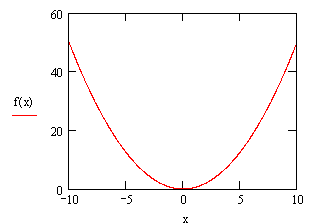
Рисунок 7.1 - Функциональная характеристикаf(x)

Плотность вероятности p_x(x) представлена на рисунке 7.2.

Рисунок 7.2 - Плотность вероятности p_x(x)

2. Найдем плотность вероятности на выходе четырехполюсника p_y(y). Для этого найдем обратную функцию :

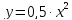(7.1)

Обратная функция х=(у) неоднозначна, т.е. одному значению y соответствует несколько значений х (рис. 11, б).

Тогда

(7.2)

Найдемp_y(y):

(7.3)

3. Cпомощью Mathcad проверим правильность найденного решения по условию нормировки:

(7.4)

ЗАДАЧА 8. Случайный стационарный процесс представлен на рисунке 8.1.

Необходимо:

1. определить автокорреляционную функцию заданного сигнала в общем виде;

2. при заданных исходных параметрах (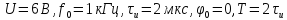) рассчитать дисперсию сигнала;

3. построить в соответствующем масштабе график автокорреляционной функции и численно определить время ее существования.

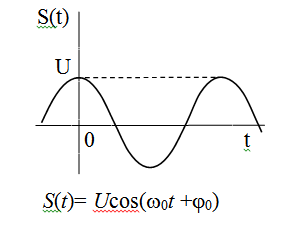
Рисунок 8.1 - Случайный стационарный процесс S(t)