Решение

1. Математическое ожидание рассчитывается по следующей формуле:

(3.1)

2. Дисперсия рассчитывается по следующей формуле:

(3.2)

ЗАДАЧА 4. На вход нелинейного элемента, вольтамперная характеристика которого приведена на рисунке 3, подается входной сигнал u_вх(t) = 2cos₁t + cos₂t.

Необходимо:

1. аппроксимировать заданную вольтамперную характеристику нелинейного элемента степенным полиномом 2-ойстепени;

2. определить ток на выходе нелинейного элемента и построить его спектрограмму;

3. по полученной аппроксимированной функции построить аппроксимированную характеристику на одном графике совместно с заданной. Из построенных графиков определить погрешность аппроксимации.

Рисунок 3 – ВАХ нелинейного элемента

Решение

1. Аппроксимируем заданную ВАХ следующим степенным полиномом:

(4.1)

Найдем коэффициенты аппроксимации, решив систему уравнения:

(4.2)

Получим:

;

;

;

.

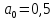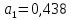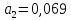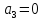Тогда аппроксимирующий полином будет иметь вид:

(4.3)

2. Подставим выражение входного сигнала в аппроксимирующую функцию:

(4.4)

Спектрограмма выходного тока имеет следующий вид:

Рисунок 4.2 – спектрограмма выходного тока

3. по полученной аппроксимированной функции построим аппроксимированную характеристику на одном графике совместно с заданной. Из построенных графиков определим погрешность аппроксимации.

Рисунок 4.3 - аппроксимированная характеристик на одном графике совместно с заданной

Погрешность аппроксимации найдем в точке i=1 графика:

(4.5)

ЗАДАЧА 5. К нелинейному элементу (рисунок 5.1), вольтамперная характеристика которого имеет кусочно-линейную аппроксимацию с напряжением запирания E_з = -0,5 В и крутизной характеристики S = 5 мА/В , приложено напряжение u_вх= (Е₀ + 2cost) В. Требуется определить:

1. смещение Е₀ и угол отсечки , при которых амплитуда 3-ей гармоники будет максимальной;

2. для определенного угла отсечки определить амплитуды гармонических составляющих тока I₀ , I₁,I₂, I₃ ;

3. по полученным величинам токов рассчитать коэффициент нелинейных искаженийk_г выходного сигнала;

4. для заданного сигнала и рассчитанного смещения Е₀ построить графически на вольтамперной характеристике сигнал на входе и выходе нелинейного устройства.

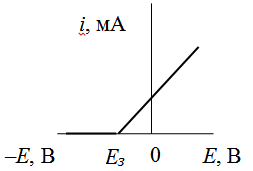
Рисунок 5.1 – кусочно-линейная аппроксимация ВАХ

Решение

1. По графику коэффициентов Берга видим, что амплитуда 2-ойгармоники будет максимальной при угле отсечки 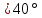. Тогда смещение E_з будет рассчитываться из выражения:

(5.1)

2. Для угла отсечки 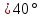определим амплитуды гармонических составляющих тока:

	(5.2)
;	(5.3)

;

;

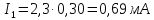3. По полученным величинам токов рассчитаем коэффициент нелинейных искаженийk_г выходного сигнала:

(5.4)

4. Сигналы на входе и выходе нелинейного устройства представлены на рисунке 5.2.

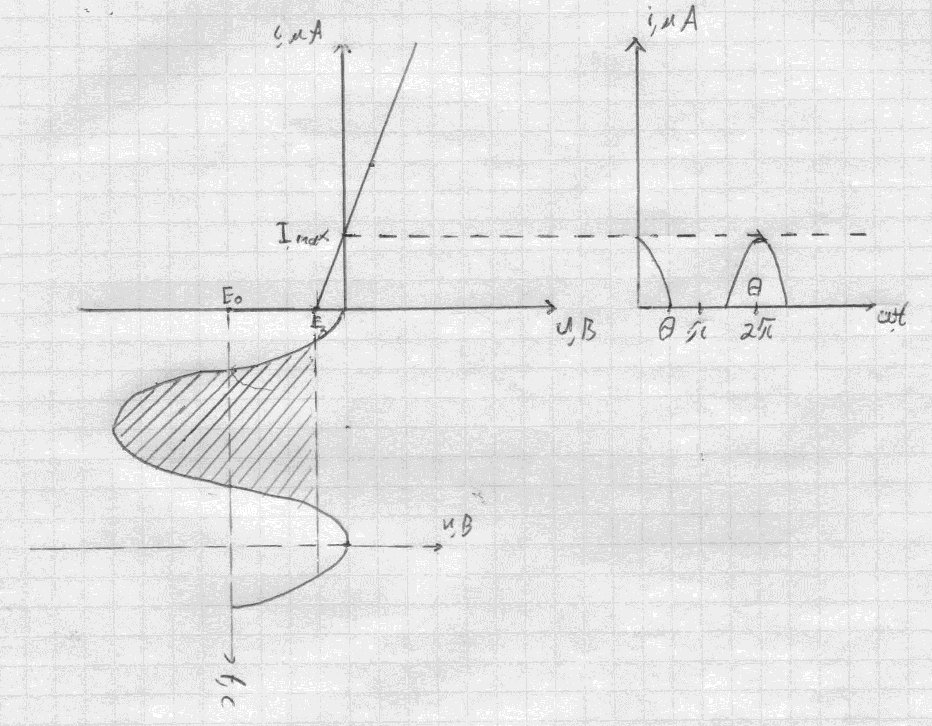
Рисунок 5.2 - Сигналы на входе и выходе нелинейного устройства

ЗАДАЧА 6. Задан узкополосный полосовой фильтр, представляющий собой параллельный резонансный колебательный контур (рисунок 6.1), имеющий неполное включение для согласования с нагрузкой R_н = 2000 Ом. Входные данные: резонансная частота 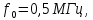входное напряжение сопротивление потерь 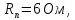емкость контура

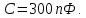
Требуется:

1. рассчитать элементы L, C1, C2, добротность Q и характеристическое сопротивление  колебательного контура, обеспечивающего согласование с сопротивлением нагрузки R_н ;

2. с учетом коэффициента включения p=0,1 определить напряжение на сопротивлении нагрузки R_н, если на вход контура подается напряжение U на резонансной частоте f₀;

3. в режиме согласования для заданного коэффициента включения p определить величину сопротивления нагрузки R_н ;

3. рассчитать и построить амплитудно-частотную (АЧХ) и фазочастотную (ФЧХ) характеристики фильтра. По этим характеристикам определить полосу пропускания фильтра на уровне 0.707 (2f_0.707) и его добротность Q. Сравнить с рассчитанным значением.

Рисунок 6.1 – узкополосный полосовой фильтр
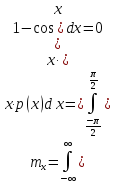
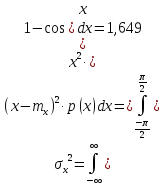
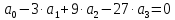
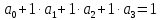
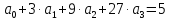
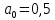
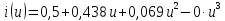
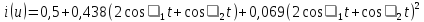
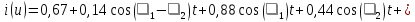
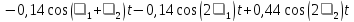
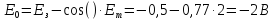
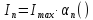