7.3. Коэффициенты корреляции рангов

Коэффициенты корреляции рангов– это менее точные, но более простые по расчету непараметрические показатели для измерения тесноты связи между двумя коррелируемыми признаками. К ним относятся коэффициенты Спирмэна (ρ) и Кендэла (τ), основанные на корреляции не самих значений коррелируемых признаков, а ихрангов– порядковых номеров, присваиваемых каждому индивидуальному значениюхиу(отдельно) в ранжированном ряду. Оба признака необходимо ранжировать (нумеровать) в одном и том же порядке: от меньших значений к большим и наоборот. Если встречается несколько значенийх(илиу), то каждому из них присваивается ранг, равный частному от деления суммы рангов (мест в ряду), приходящихся на эти значения, на число равных значений. Ранги признаковхиуобозначают символамиR_xиR_y(иногдаN_xиN_y). Суждение о связи между изменениями значенийхиуосновано на сравнении поведения рангов по двум признакам параллельно. Если у каждой парыхиуранги совпадают, это характеризует максимально тесную связь. Если же наблюдается полная противоположность рангов, т.е. в одном ряду ранги возрастают от 1 доn, а в другом – убывают отnдо 1, это максимально возможная обратная связь. Подходы для оценки тесноты связи у Спирмэна и Кендэла несколько различаются. Для расчетакоэффициента Спирмэназначения признаковхиунумеруют (отдельно) в порядке возрастания от 1 доn, т.е. им присваивают определенный ранг (R_xиR_y) – порядковый номер в ранжированном ряду. Затем для каждой пары рангов находят их разность (обозначается какd= R_x–R_y), и квадраты этой разности суммируют.

, (2)

где d – разность рангов х и у;

n – число наблюдаемых пар значений х и у.

Коэффициент ρможет принимать значения от 0 до ±1. Следует иметь в виду, что, поскольку коэффициент Спирмэна учитывает разность только рангов, а не самих значенийх иу, он менее точен по сравнению с линейным коэффициентом. Поэто­му его крайние значения (1 или 0) нельзя безоговорочно расцени­вать как свидетельство функциональной связи или полного от­сутствия зависимости междух и у. Во всех других случаях, т.е. когдаρ не принимает крайних зна­чений, он довольно близок кr.

Формула (2) применима строго теоретически только тогда, когда отдельные значения х (и у), а следовательно, и их ранги не повторяются. Для случая повторяющихся (связанных) рангов есть другая, более сложная формула, скорректированная на число по­вторяющихся рангов. Однако опыт показывает, что результаты расчетов по скорректированной формуле для связанных рангов мало отличаются от результатов, полученных по формуле для не­повторяющихся рангов. Поэтому на практике формула (2) ус­пешно применяется как для неповторяющихся, так и для повто­ряющихся рангов.

Коэффициент корреляции рангов Кендэла τ строится несколь­ко по-другому, хотя его расчет также начинается с ранжирования значений признаков х и у. Ранги х (R_x) располагают строго в порядке возрастания и па­раллельно записывают соответствующее каждому R_x значение R_y. Поскольку R_x записаны строго по возрастанию, то ставится задача определить меру соответствия последовательности R_y «пра­вильному» следованию R_x. При этом для каждого R_y последо­вательно определяют число следующих за ним рангов, превыша­ющих его значение, и число рангов, меньших по значению. Первые («правильное» следование) учитываются как баллы со знаком «+», и их сумма обозначается буквой Р. Вторые («непра­вильное» следование) учитываются как баллы со знаком «–», и их сумма обозначается буквой Q. Очевидно, что максимальное значение Р достигается в том слу­чае, если ранги y (R_y) совпадают с рангами х (R_x) и в каждом ряду представляют ряд натуральных чисел от 1 до п. Тогда после первой пары значений R_x = 1 и R_y = 1 число превышения данных значений рангов составит (n – 1), после второй пары, где R_x = 2 и R_y = 2, соответственно (п – 2) и т.д. Таким образом, если ранги х и у совпадают и число пар рангов равно n, то

.

Если же последовательность рангов хиуимеет обратную тенденцию по отношению к последовательности ранговх, тоQбудет такое же максимальное значение по модулю:

.

Если же ранги у не совпадают с рангами х, то суммируются все положительные и отрицательные баллы (S=P+Q); отношение этой суммыSк максимальному значению одного из слагаемых и представляет собой коэффициент корреляции рангов Кендэла τ, т.е.:

. (2)

Формула коэффициента корреляции рангов Кендэла (2) применяется для случаев, когда отдельные значения признака (как х, так иу) не повторяются и, следовательно, их ранги не объе­динены. Если же встречается несколько одинаковых значенийх (илиу), т.е. ранги повторяются, становятсясвязанными, коэффици­ент корреляции рангов Кендэла определяется по формуле:

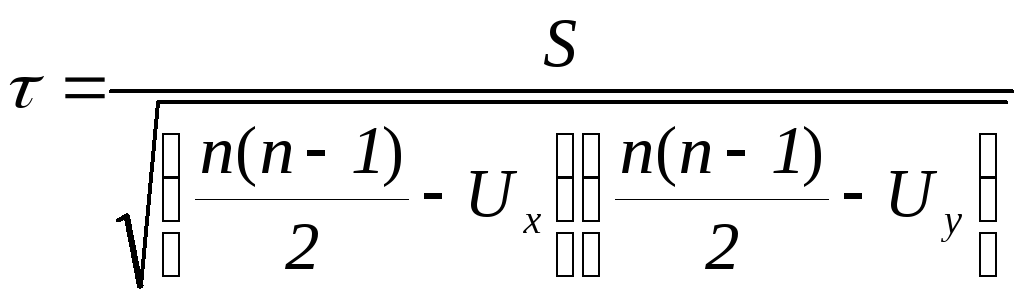,(2)

где S – фактическая общая сумма баллов при оценке +1 каж­дой пары рангов с одинаковым порядком изменения и –1 каждой пары рангов с обратным порядком изме­нения;

– число баллов, корректирующих (уменьшающих) максимальную сумму баллов за счет повторений (объединений)t рангов в каждом ряду.

Отметим, что случаи следования одинаковых повторяющихся рангов (в любом ряду) оцениваются баллом 0, т.е. они не учиты­ваются при расчете ни со знаком «+», ни со знаком «–».

Преимущества ранговых коэффициентов корреля­ции Спирмэна и Кендэла: они легко вычисляются, с их помощью можно изучать и измерять связь не только между количественны­ми, но и между качественными (описательными) признаками, ранжированными определенным образом. Кроме того, при ис­пользовании ранговых коэффициентов корреляции не требуется знать форму связи изучаемых явлений.

Если число ранжируемых признаков (факторов) больше двух, то для измерения тесноты связи между ними можно использовать предложенный М. Кендэлом и Б. Смитом коэффициент конкордации (множественный коэффициент ранговой корреляции):

,(2)

где S — сумма квадратов отклонений суммы т рангов от их средней величины;

т — число ранжируемых признаков;

п — число ранжируемых единиц (число наблюдений).

Формула (2) применяется для случая, кода ранги по каж­дому признаку не повторяются. Если же есть связанные ран­ги, то коэффициент конкордации рассчитывается с учетом числа таких повторяющихся (связанных) рангов по каждому фактору:

, (2)

где t – число одинаковых рангов по каждому признаку.

Коэффициент конкордации Wможет принимать значения от 0 до 1. Однако, необходимо проверить его на существенность (значимость) с помощью критерия χ²при отсутствии связанных рангов по формуле (2), а при их наличии – по формуле (2):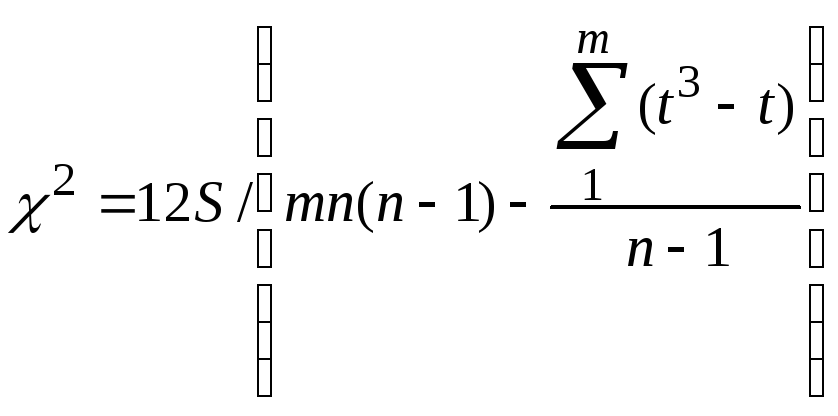

, (2). (2)

Фактическое значение χ²сравнивается с табличным, соответ­ствующим принятому уровню значимостиα(0,05 или 0,01) и числу степеней свободыv=п –1. Если χ²_факт> χ²_табл, тоW – существенен (значим).

Коэффициент конкордации особенно часто используется в экспертных оценках, например, для того, чтобы определить сте­пень согласованности мнений экспертов о важности того или иного оцениваемого показателя или составить рейтинг отдельных единиц по какому-либо признаку. В формуле (2) в этих случаях т означает число экспертов, а n — число ранжируемых единиц (или признаков).