
Робота №1
Тема: Математична модель на ПЕОМ
Ціль: Оволодіння практичними навичками розрахунків і графічного відображення функціональної залежності у вигляді імітаційної моделі на ЕОМ у розрахунковій системі “EXCEL”.
Задача: Побудувати на ПЕОМ модель процесу поливу дощуванням, який характеризується параметрами: інтенсивність дощу, вбирання води ґрунтом та тривалість поливу. Модель представити у вигляді:
|
Вхідні данні Розрахункові дані:
Вихідні дані: графічне відображення параметрів поливу  
|
Для розрахунку використані наступні формули :

де : t - час від початку поливу,
Кз - швидкість усмоктування води ґрунтом при затопленні,
Кд - швидкість усмоктування води ґрунтом при дощуванні,
r - інтенсивності дощу,
tm - тривалість поливу нормою m.
Модель процесу поливу дощуванням
1.Вихідні дані
|
0,04 |
Швидкість вбирання грунтом в кінці 1години , м/год |
К1 |
|
0,7 |
Коефіцієнт зміни швидкості вбирання |
α |
|
0,8 |
Коефіцієнт зменшення швидкості вбирання |
λ |
|
0,25 |
Середня інтенсивність дощу , мм/хв. |
r |
|
300 |
Поливна норма , м3/га |
m |
2.Розрахункові дані
|
0,125 |
0,25 |
0,50 |
1,00 |
2,00 |
3,00 |
4,00 |
t,год |
|
2,86 |
1,76 |
1,09 |
0,67 |
0,41 |
0,31 |
0,25 |
Кз,мм/хв |
|
2,29 |
1,41 |
0,87 |
0,53 |
0,33 |
0,25 |
0,20 |
Кд,мм/хв |
|
0,25 |
0,25 |
0,25 |
0,25 |
0,25 |
0,25 |
0,25 |
r, мм/хв |
|
7,50 |
15,00 |
30,00 |
60,00 |
120,00 |
180,00 |
240,00 |
t,хв |
|
|
|
|
|
|
|
120,00 |
tm,хв |
|
|
|
|
|
|
0,25 |
120,00 |
A(r,tm) |
3.Вихідні дані у вигляді графічного відображення параметрів поливу
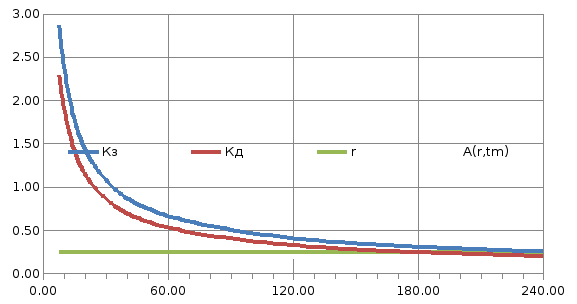
4. Аналіз взаємодії інтенсивності дощу та швидкості вбирання води ґрунтом вказує на те що на 180 хвилині ці параметри урівнюються і в подальшому утворюється поверхневий стік. За цім часом встановлюємо допустиму поливну норму до появи стоку:
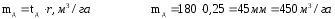
Робота №2
Тема: Статистична обробка імовірнісного ряду
Ціль: Оволодіння практичними навичками обчислення основних статистичних характеристик і побудова моделі імовірнісного ряду.
Задача: Для гідрологічного ряду складеного з дефіциту водного балансу поля зайнятого с-г культурою (W):
установити основні статистичні характеристики,
побудувати графік нормального розподілу ( крива забезпеченості),
установити емпіричні і теоретичні значення для умов: середньо-посушливого, посушливого й гостро-засушливого років (75%, 85%, 95% забезпеченості),
установити роки з дефіцитом водного балансу зазначеної забезпеченості.
Для виконання роботи будемо використовувати наступні формули і функції :
1.Середнє арифметичне значення ( СРЗНАЧА= )
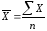 ;
де n – кількість членів ряду.
;
де n – кількість членів ряду.
2.Стандартне відхилення ( СТАНДОТКЛОНА= )
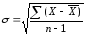 .
.
3.Коефіцієнт варіації (мінливості) ряду
 ,
,
а мінливість ряду вважається: не значна якщо V < 10%
середня V = 10 - 20%
значна V > 20%
4.Нормальна функція розподілу для кожного члена гідрологічного ряду за основними статистичними показниками ( НОРМРАСПР = )
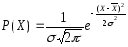
де : σ – стандартне відхилення,
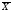 -
середнє арифметичне,
-
середнє арифметичне,
e = 2,72 – основа натурального логарифма.
5.Визначимо роки, у які спостерігався дефіцит водного балансу із забезпеченістю - 75%, 85% і 95% , використовуючи при цьому функцію зворотного стандартного нормального розподілу ( НОРМОБР = ).
|
Календарний рік |
1978 |
1979 |
1980 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
|
ΔW,мм |
160 |
287 |
165 |
281 |
125 |
231 |
238 |
82 |
315 |
219 |
167 |
365 |
306 |
144 |
260 |
231 |
345 |
354 |
482 |
87 |
480 |
420 |
287 |
414 |
360 |
2.Статистичні характеристики
|
Середнє арифметичне |
272,2 |
|
|
Стандартне відхилення |
114,06 |
|
|
Коефіцієнт варіації ряду |
41,902 |
˃20% мінливість ряду значна |
3,4.Варіаційний ряд дефіциту водного балансу та нормальний розподіл
|
Календарний рік |
1978 |
1979 |
1980 |
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
|
ΔW,мм |
82 |
87 |
125 |
144 |
160 |
165 |
167 |
219 |
231 |
231 |
238 |
260 |
281 |
287 |
287 |
306 |
315 |
345 |
354 |
360 |
365 |
414 |
420 |
480 |
482 |
|
Нормальній розподіл |
4,77 |
5,22 |
9,84 |
13,05 |
16,26 |
17,36 |
17,82 |
32,05 |
35,90 |
35,90 |
38,21 |
45,74 |
53,07 |
55,16 |
55,16 |
61,65 |
64,63 |
73,84 |
76,34 |
77,93 |
79,21 |
89,31 |
90,25 |
96,58 |
96,71 |
5.Графічне відображення функції нормального розподілу

|
75% |
85% |
95% |
Забезпеченість , % |
|
1996 |
1999 |
2001 |
Роки |
|
354 |
414 |
480 |
Емпіричні значення , мм |
|
350 |
394 |
468 |
Теоретичні значення , мм |
Робота №3
Тема: Обчислення коефіцієнта кореляції і рівняння регресії
Ціль: Оволодіння практичними навичками обчислення кореляційного зв'язку між ознаками і представлення його у вигляді математичної моделі і графічно.
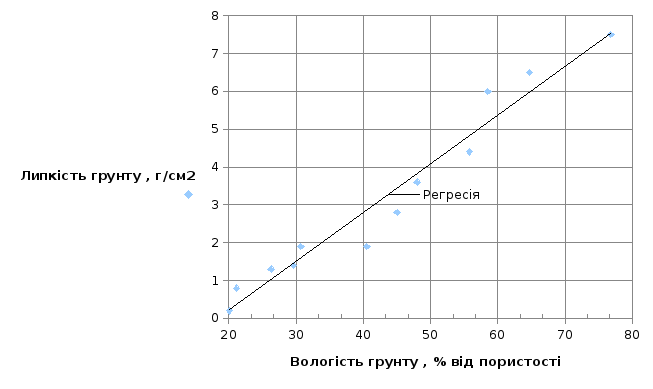
Задача: Установити параметри кореляційного зв'язку між водно-фізичними властивостями ґрунту – липкістю і вологістю:
коефіцієнт кореляції і тісноту зв'язку,
коефіцієнт регресії і рівняння регресії.
Для розрахунку будемо використовувати наступні формули та функції :
1.Коефіцієнт кореляції (КОРРЕА = ) і дамо оцінку кореляційного зв'язку між ознаками
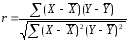
r < 0,3 - слабкий
r = 0,3 – 0,7 - середній
r > 0,7 - сильний
2. Коефіцієнт регресії ( НАХИЛ = )

3.
Середні арифметичні значення ознак
 (СРЗНАЧА = ) і складемо рівняння регресії
(СРЗНАЧА = ) і складемо рівняння регресії
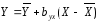
Обчислення параметрів кореляційного зв'язку між ознаками
1. Вихідні дані
Х – вологість ґрунту, % від пористості,
Y – липкість ґрунту, г/см2
|
X |
20,1 |
21,1 |
26,3 |
29,6 |
30,7 |
40,5 |
45 |
48 |
55,8 |
58,5 |
64,7 |
76,8 |
|
Y |
0,2 |
0,8 |
1,3 |
1,4 |
1,9 |
1,9 |
2,8 |
3,6 |
4,4 |
6 |
6,5 |
7,5 |
|
Yp |
0,22 |
0,35 |
1,02 |
1,45 |
1,59 |
2,86 |
3,44 |
3,83 |
4,83 |
5,18 |
5,98 |
7,54 |
2.Коефіцієнт кореляції
|
r = |
0,98 |
˃ 0,7 зв'язок між ознаками значний |
3.Коефіцієнт регресії
|
byx = |
0,13 |
|
4.Середнє арифметичне та рівняння регресії
|
|
3,1916667 |
|
|
43,091667 |
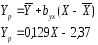
Робота №4
Тема: Регресійне моделювання імовірнісних зв'язків
Ціль: Оволодіння практичними навичками вибору математичної моделі імовірнісного зв'язку між явищами в меліорації.

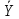 =
=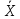 =
=