ИДЗ №8 по теме «Ряды».
Основные теоретические сведения.
Определение.
Сумма членов бесконечной числовой
последовательности
называетсячисловым
рядом.
(1.1)
При
этом числа
будем называть членами ряда, аun
– общим членом ряда.
Определение.
Суммы
,n
= 1, 2, …
называются частными
(частичными) суммами ряда.
Таким образом, возможно рассматривать последовательности частичных сумм ряда S1, S2, …,Sn, …
Определение.
Ряд
называетсясходящимся,
если сходится последовательность его
частных сумм. Сумма
сходящегося ряда
– предел последовательности его частных
сумм.
Определение. Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммы.
Пример 1.
Ряд
сходится, так как представляет собой
бесконечно убывающую геометрическую
прогрессию со знаменателем
,
сумму которой можно найти по формуле
.
Пример 2.
Рассмотрим ряд
.
Представим общий член ряда в виде:
.
Тогда частичная суммаsn
будет выглядеть так:
.
Тогда
.
Следовательно, ряд сходится, и его сумма
равна
.
Пример 3.
Ряд 1+1+1+…+1+… расходится, так как
Пример 4. Ряд 1-1+1-1+…+(-1)п+1+… тоже расходится, так как последовательность его частичных сумм имеет вид: s1 = 1, s2 = 0, s3 = 1, s4 = 0 и т.д., а такая последовательность предела не имеет.
Ряд, полученный из (1.1) отбрасыванием первых его m членов, называется остатком ряда (1.1):
(1.2)
Свойства рядов.
1) Сходимость или расходимость ряда не нарушится, если изменить, отбросить или добавить конечное число членов ряда.
2)
Рассмотрим два ряда
и
,
где С – постоянное число.
Теорема.
Если ряд
сходится
и его сумма равнаS,
то ряд
тоже
сходится, и его сумма равна СS.
(C
0)
3)
Рассмотрим два ряда
и
.Суммой
или разностью
этих рядов будет называться ряд
,
где элементы получены в результате
сложения (вычитания) исходных элементов
с одинаковыми номерами.
Теорема.
Если ряды
и
сходятся
и их суммы равны соответственноS
и ,
то ряд
тоже сходится и его сумма равнаS
+ .
Разность двух сходящихся рядов также будет сходящимся рядом.
Сумма сходящегося и расходящегося рядов будет расходящимся рядом.
О сумме двух расходящихся рядов общего утверждения сделать нельзя.
3) Ряд сходится или расходится вместе со своим остатком (1.2).
При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
Критерий Коши.(необходимое и достаточное условие сходимости ряда)
Для
того, чтобы ряд
был
сходящимся необходимо и достаточно,
чтобы для любого
существовал номерN
такой, что при n>N
и любом p>0
выполнялось бы неравенство
.
Однако, на практике использовать непосредственно критерий Коши не очень удобно. Поэтому, как правило, используются более простые признаки сходимости.
Необходимый признак сходимости ряда
Теорема 1. Если ряд (1.1) сходится, то его общий член стремится к нулю:
(1.3)
Следствие.
Если
,
то ряд (1.1) расходится.
Пример 5.
Исследовать сходимость ряда
Найдем
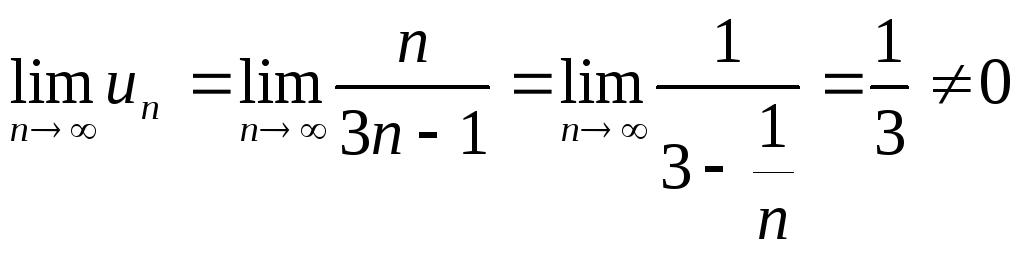- необходимый признак сходимости не
выполняется. Значит ряд расходится.
Пример. 6.
Исследовать сходимость ряда
.
Найдем:
(в числителе стоит показательная функция,
которая растет быстрее, чемn),
следовательно, ряд расходится.
Пример. 7.
Исследовать сходимость гармонического
ряда
.
Очевидно, условие
(1.3) выполняется:
,
однако, гармонический ряд расходится.
Действительно, если предположить, что
ряд сходится и его сумма равнаS,
то
.
Тогда из неравенства
.
Получили противоречие.
Замечание. Существуют и другие методы доказательства расходимости гармонического ряда.
Знакоположительные ряды
Ряд
называетсязнакоположительным,
если
.
Достаточные признаки сходимости знакоположительных рядов.
Теорема 2. (признак сравнения в непредельной форме).
Даны 2 ряда
(а)
и
(b).
Если, начиная с некоторого n,
выполняется условие
и ряд (b)
сходится, то сходится и ряд (а). Если же
ряд (а) расходится, то ряд (b)
тоже расходится.
Теорема 3. (признак сравнения в предельной форме).
Даны 2 ряда
(a)
и
(b).
Если существует конечный и не равный
нулю предел:
,
то ряды (а) и (b)
сходятся или расходятся одновременно.
В качестве рядов для сравнения удобно выбирать:
гармонический ряд
,
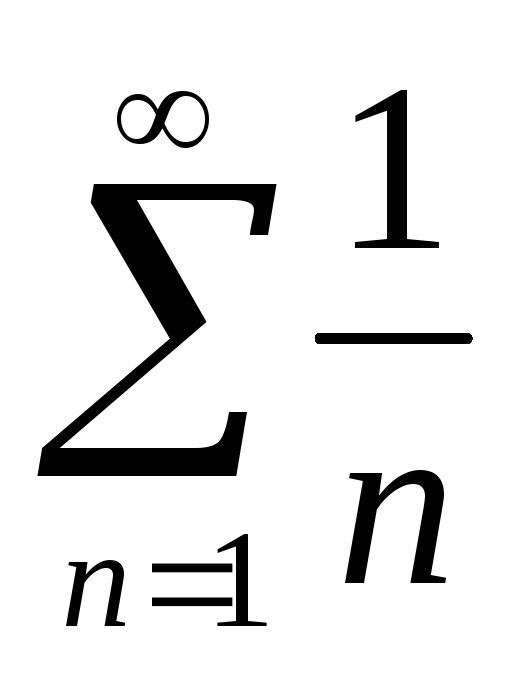который расходится;обобщенный гармонический ряд
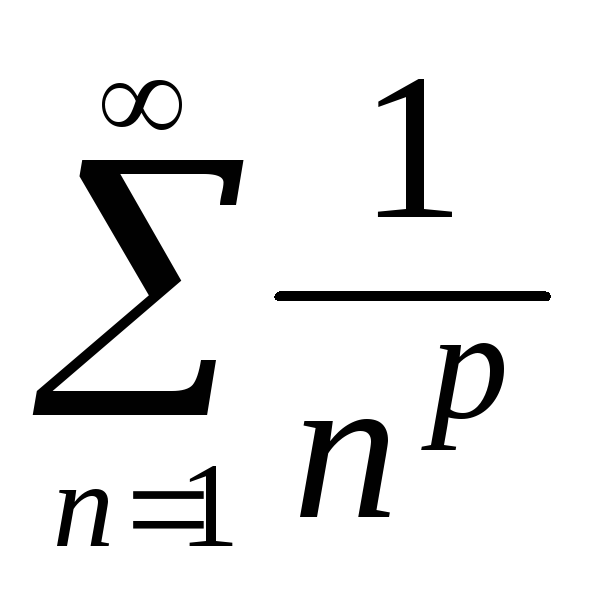(ряд Дирихле), который сходится приp>1
и расходится при p1;
3) геометрическую
прогрессию
,
которая сходится, если
и
расходится, если
.
Признак сравнения в предельной форме особенно эффективен для рядов, общий член которых есть алгебраическая функция целого аргумента, либо функция, в пределе приводимая к вышеуказанной (использование таблицы эквивалентных бесконечно малых), т.к. позволяет свести исследование сходимости исходного ряда к рассмотрению одного из трех “эталонных” рядов.
Пример
8.
Исследовать на сходимость ряд
Т.к.
,
а гармонический ряд
расходится, то расходится и ряд
.
Пример
9.
Исследовать
на сходимость ряд
Т.к.
,
а ряд
сходится ( как убывающая геометрическая
прогрессия), то ряд
тоже сходится.
Пример 10.
Исследовать сходимость ряда
.
Ряд знакоположительный,
применим к нему признак сравнения в
предельной форме, сравнив его с рядом
,
который сходится как обобщенный
гармонический ряд с
.
.
Предел отношения общих членов этих
рядов при
конечный, не равный нулю, следовательно,
ряды ведут себя одинаково; данный ряд
сходится. Ряд для сравнения подбираем
следующим образом: при
;
Пример 11.
Исследовать сходимость ряда
.
Ряд знакоположительный.
Т.к. при
аргумент
,
то
,
поэтому для сравнения берем ряд
.
Последний ряд является гармоническим,
все члены которого умножены на
,
что не влияет на его расходимость. Т.к.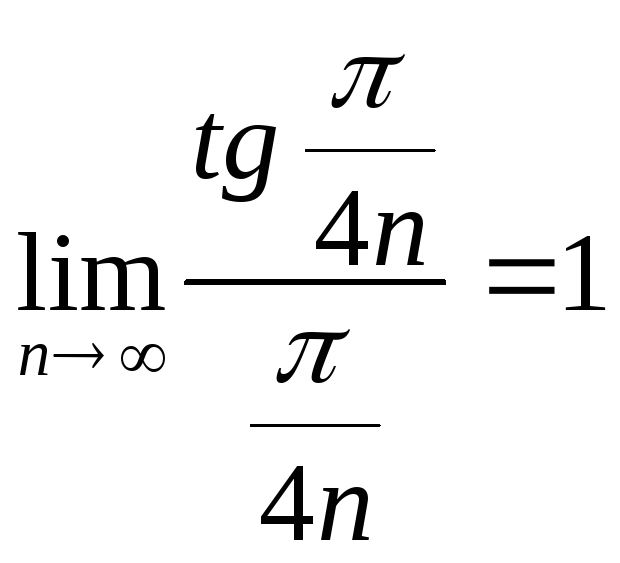
и ряд
расходится, то
также расходится.
Пример 12.
Исследовать на сходимость ряд
.
Ряд дан
знакоположительный. Т.к.
,
т.е. он может быть равен 1 или–1, то
.
Из последнего неравенства видно, что
исходный ряд можно сравнить с рядом
,
а этот ряд сходится (обобщенный
гармонический сp=2>1,
все члены которого умножены на 4). Но
т.к. ряд
с большими членами сходится, то на
основании признака сравнения в
непредельной форме будет сходиться и
исходный ряд.
Теорема 4. (признак Даламбера).
Дан ряд
(un
>0). Если
существует
,
то приl<1
ряд сходится, при l>1
ряд расходится; при l=1
вопрос о сходимости ряда остается
открытым.
Пример
13.
Определить сходимость ряда
.
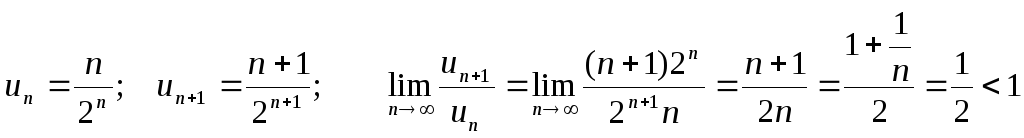
Вывод: ряд сходится.
Пример
14.
Определить сходимость ряда
Вывод: ряд сходится.
Пример
15.
Применим признак Даламбера к исследованию
сходимости ряда
.
, следовательно,
ряд сходится
(учитываем, что (п + 1)! = п!(п + 1) ).
Признак эффективен в случае наличия в общем члене ряда показательной функции или факториалов.
Пример 16. Исследовать сходимость ряда
c помощью признака Даламбера.
Здесь
.
Тогда
.
Ряд сходится, т.к. q<1.
Пример
17.
Исследовать сходимость ряда
.
,
=
.
Т.к. l>1,
ряд расходится.
Теорема 5 (признак Коши, радикальный).
Дан ряд
(un
>0). Если
существует
,
то приl<1
ряд сходится; при l>1
ряд расходится; при l=1
вопрос о сходимости ряд остается
открытым.
Радикальный признак Коши дает результат в случае, когда общий член ряда имеет вид степенно-показательной функции целочисленного аргумента.
Пример
18.
Определить сходимость ряда
.
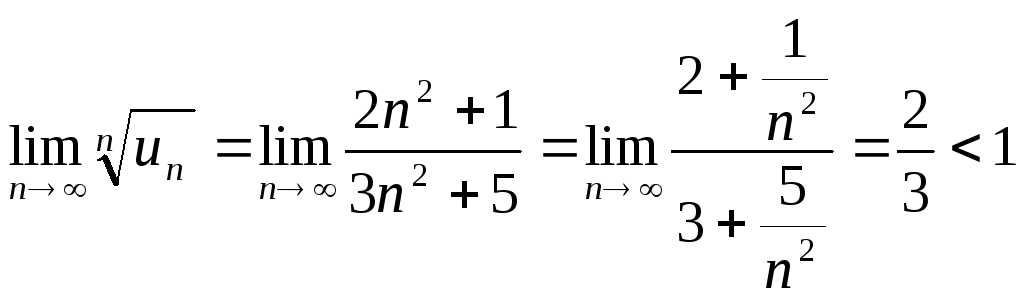
Вывод: ряд сходится.
Пример
19.
Определить сходимость ряда
.
Т.е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю.
,
таким образом, необходимое условие сходимости не выполняется, значит, ряд расходится.
Пример
20.
Для ряда
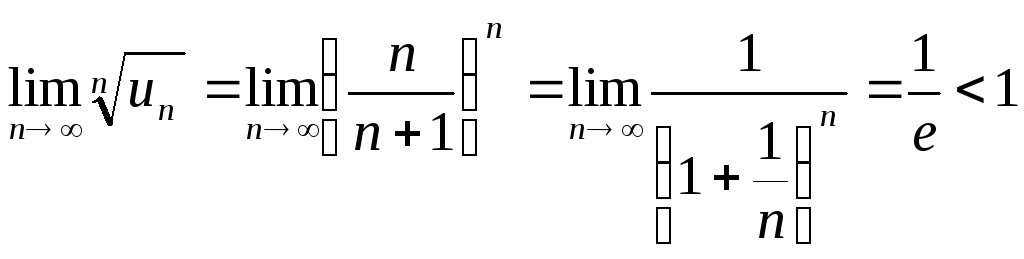- ряд сходится.
Пример 21.
Исследовать сходимость ряда
.
Ряд знакоположительный, применим к нему признак Коши; найдем
.По
теореме 5 ряд сходится.
Теорема 6 (интегральный признак Коши).
Если функция f
неотрицательна и убывает на полупрямой
х
≥ 1, то ряд
сходится или расходится одновременно
с несобственным интегралом
.
Следствие. Если функция y=f(x) удовлетворяет следующим условиям
1)
;
2) непрерывна, положительна и монотонно
убывает при
,
то ряд и несобственный интеграл
одновременно сходятся или расходятся.
Интегральный признак Коши удобно применять в тех случаях, когда функция f(x), полученная заменой в общем члене ряда целочисленной переменнойnна непрерывную переменнуюx, обладает легко находимой первообразной.
Пример
22. Применим
интегральный признак Коши к исследованию
сходимости рядов вида
,
сравнивая их с интегралами
Рассмотрим следующие возможные значения
α:
а)
α > 1. Тогда
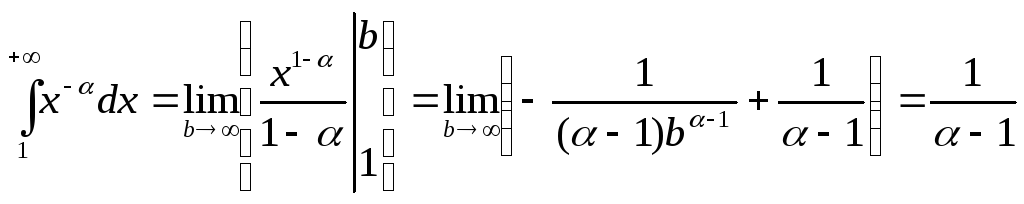(так как при α>1
).
Следовательно, несобственный интеграл
сходится, а значит, сходится и
рассматриваемый ряд.
б)
α = 1. При этом
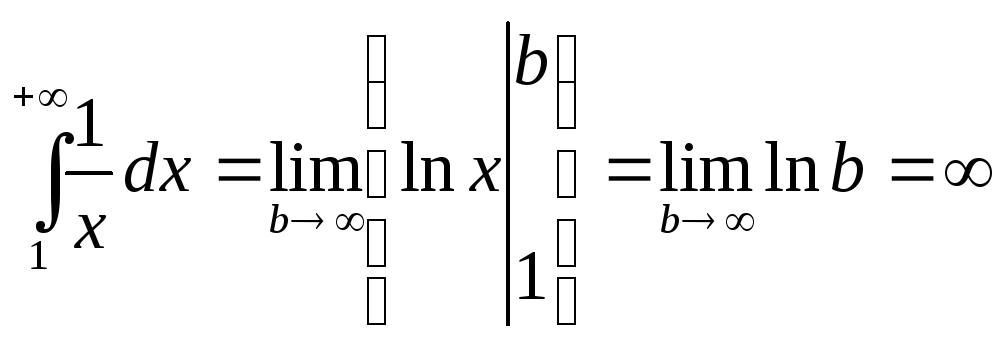- интеграл расходится, поэтому расходится
и ряд.
в)
α < 1. Тогда
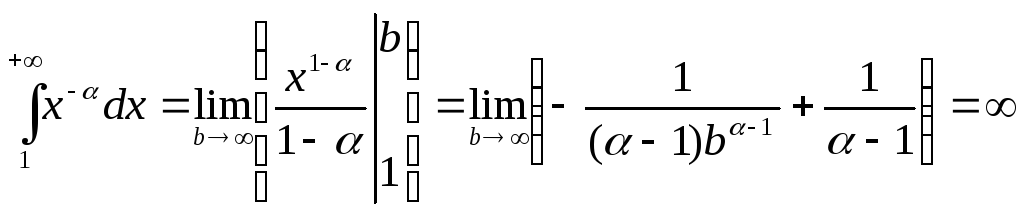(так как при α < 1
).
Из расходимости несобственного интеграла
следует расходимость исследуемого
ряда.
Замечание.
Итак, ряд вида
сходится при
α > 1 и расходится при α ≤ 1. Это
свойство ряда
будет часто использоваться в дальнейшем.
Пример 23.
Исследовать сходимость ряда
.
Рассмотрим
функцию
.
При натуральных значениях аргумента
значения функции совпадают с
соответствующими членами ряда:
.
Кроме того,f(x)
при
будет
непрерывной, положительной и монотонно
убывающей (функция
,
стоящая в знаменателе, растет быстрее,
чемln(x+1),
стоящая в числителе). Показать, что f(x)
будет монотонно убывающей, можно и с
помощью
:
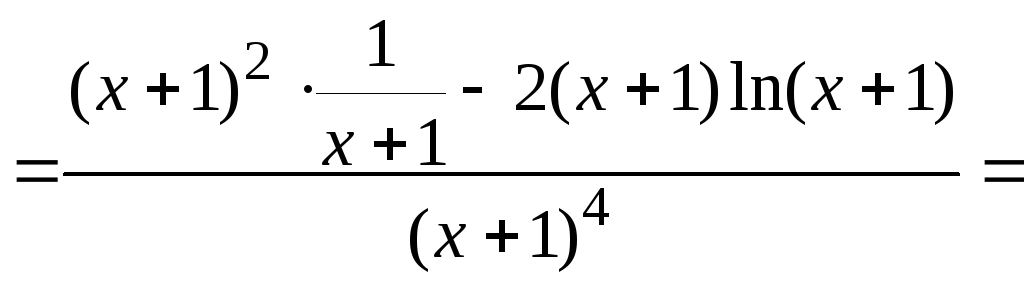
для
,
следовательно,f(x)
- убывающая на [1,+).
Рассмотрим
несобственный интеграл
,
который берется по частям:
.
Найдем отдельно
.
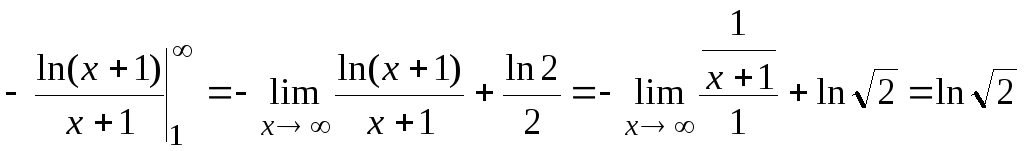Здесь для нахождения
предела применили правило Лопиталя.
Далее:
.
Итак,
=
.
Интеграл сходится, следовательно,
сходится и данный ряд.