
- •Неопределенный интеграл. Основные понятия
- •Свойства неопределенного интеграла
- •2. Методы интегрирования Простейшие методы интегрирования
- •Интегрирование по частям
- •Интегрирование рациональных функций
- •Интегрирование простейших функций, содержащих квадратный трехчлен.
- •Интегрирование некоторых иррациональных функций.
Неопределенный интеграл. Основные понятия
Неопределенным
интегралом
от функции
![]() на промежуткеX
называется множество всех первообразных
для функции
на промежуткеX
называется множество всех первообразных
для функции
![]() .
Неопределенный интеграл обозначается
символом
.
Неопределенный интеграл обозначается
символом![]() .
.
Функция
F(x)
называется первообразной
функцией для функции
![]() на промежуткеX,
если в каждой точке x
этого промежутка
на промежуткеX,
если в каждой точке x
этого промежутка
![]() .
.
Тогда по определению неопределенного интеграла получим
![]() ,
,
где C – произвольная постоянная.
Интегральное исчисление решает задачу обратную задаче дифференциального исчисления. Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Основной задачей интегрального исчисления является нахождение самой функции по ее производной или дифференциалу.
Отсюда заключаем, что правильность результата интегрирования может быть проверена дифференцированием, то есть вычислением производной найденной первообразной.
Свойства неопределенного интеграла
10. Производная от неопределенного интеграла равна подынтегральной функции:
![]()
20. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
![]()
30. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянного слагаемого:
![]()
40. Постоянный множитель можно выносить за знак неопределенного интеграла:
![]()
50. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен сумме неопределенных интегралов от этих функций:
![]()
60.
Если
![]() ,
то
,
то![]() ,
гдеa,
b
– постоянные
числа, причем
,
гдеa,
b
– постоянные
числа, причем
![]() .
.
70.
Если
![]() ,
то
,
то![]() ,
где
,
где![]() - любая дифференцируемая функция.
- любая дифференцируемая функция.
Таблица основных неопределенных интегралов
Если
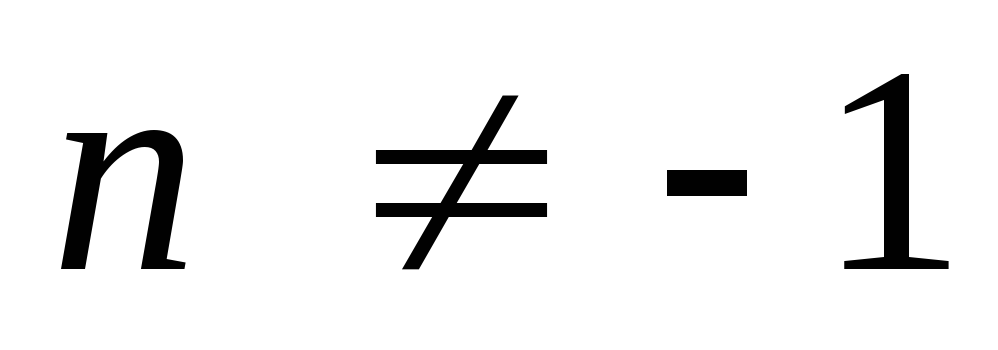 ,
то
,
то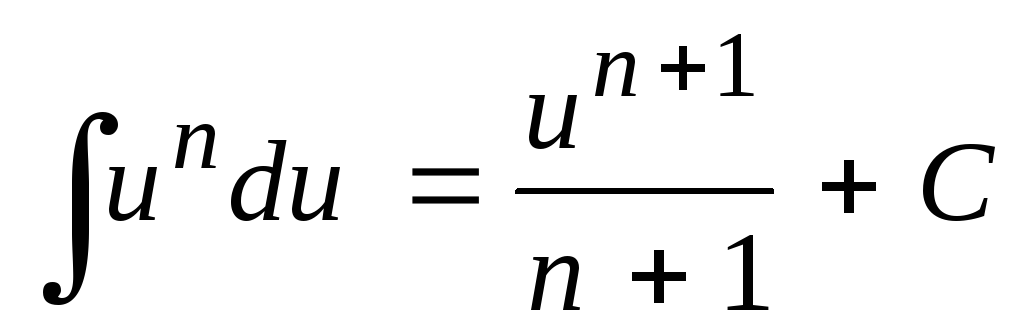 ;
;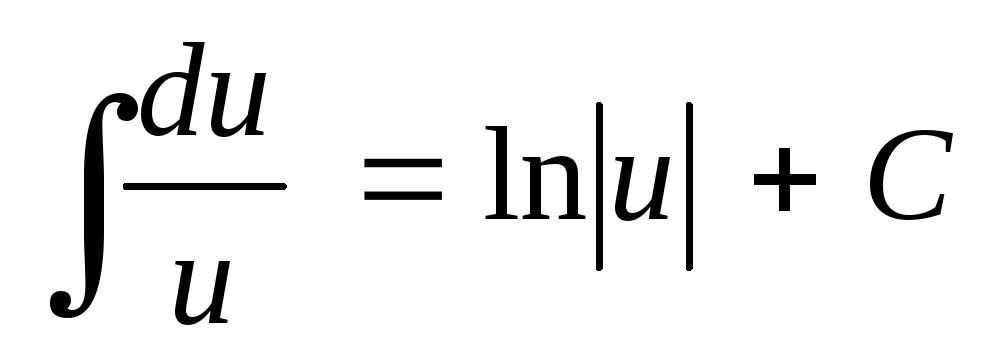 ;
;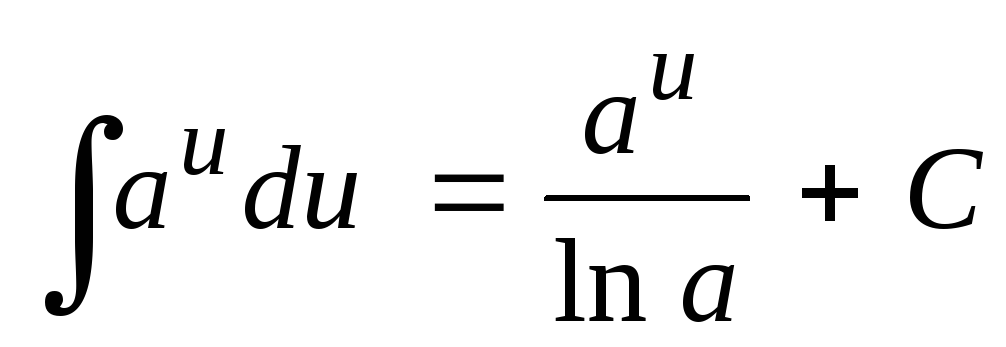 ;
;
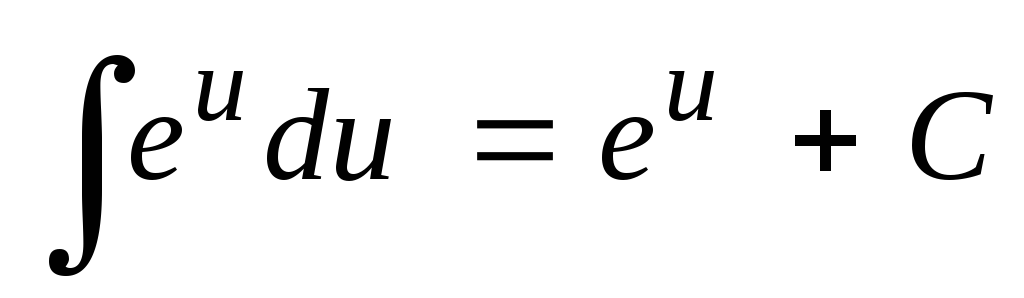 ;
; ;
;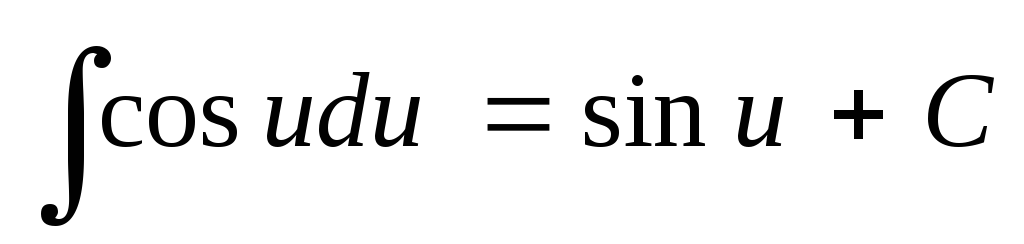 ;
;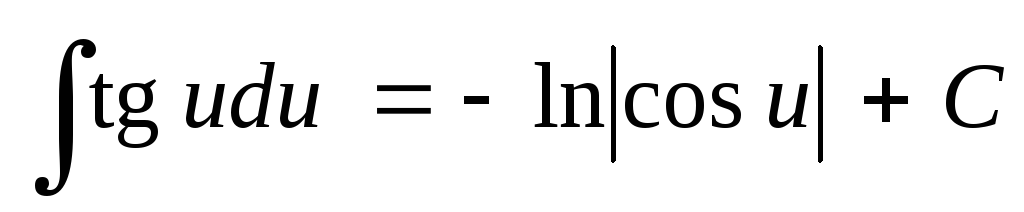 ;
;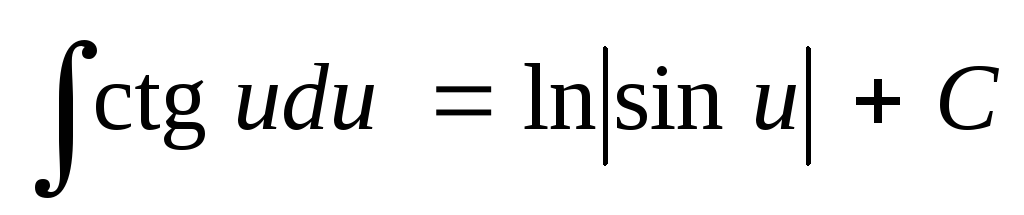 ;
;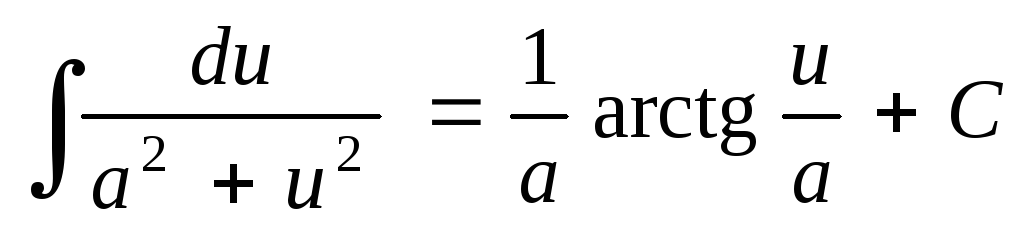 ;
;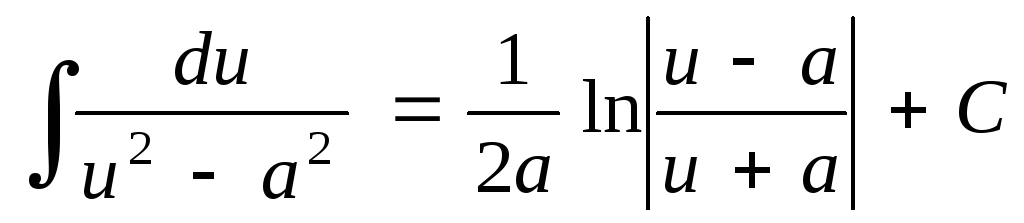 ;
;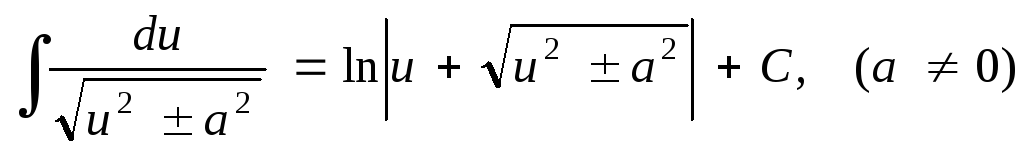 ;
;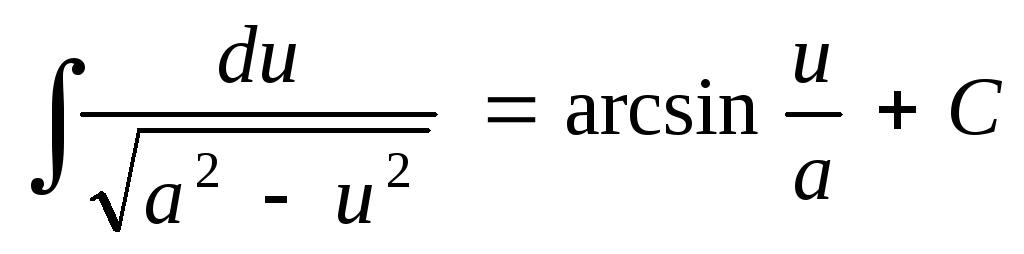 ;
;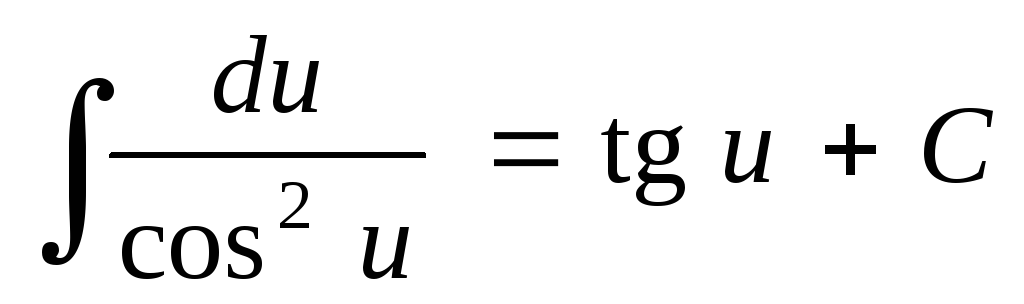 ;
;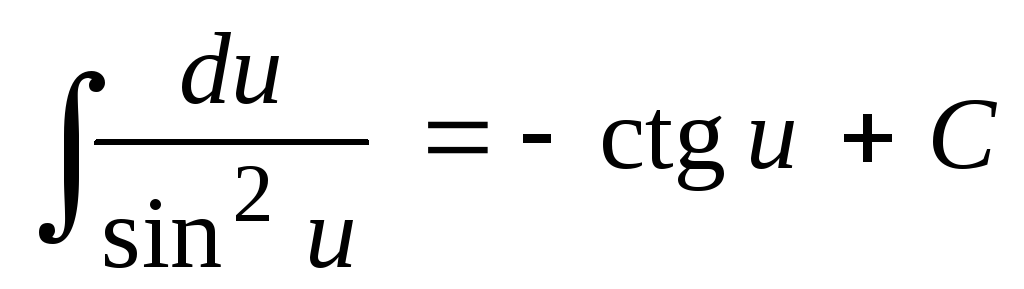 ;
;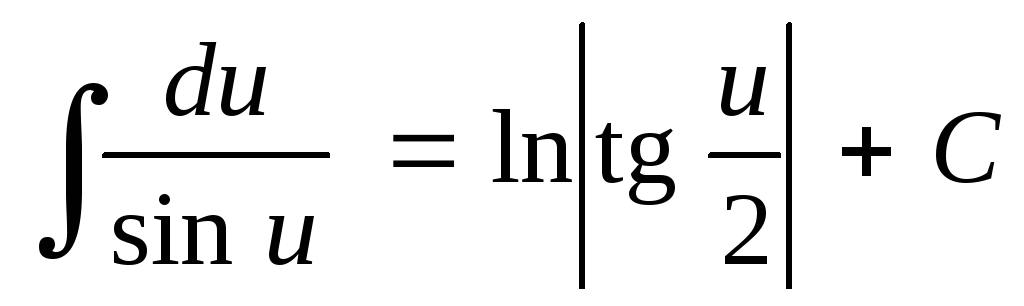 ;
;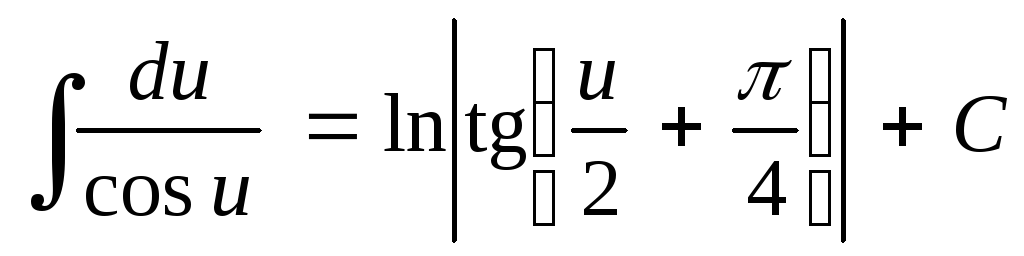 ;
;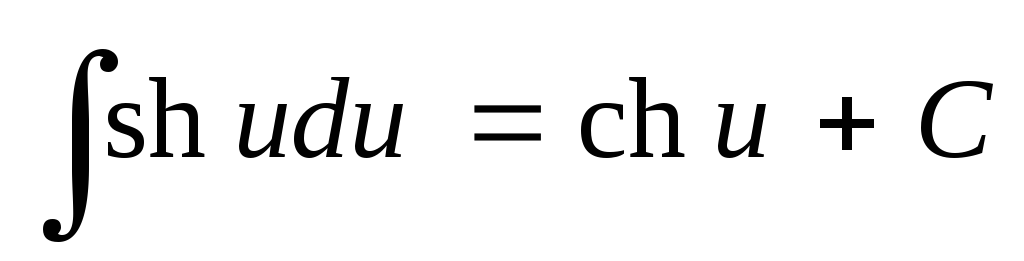 ;
;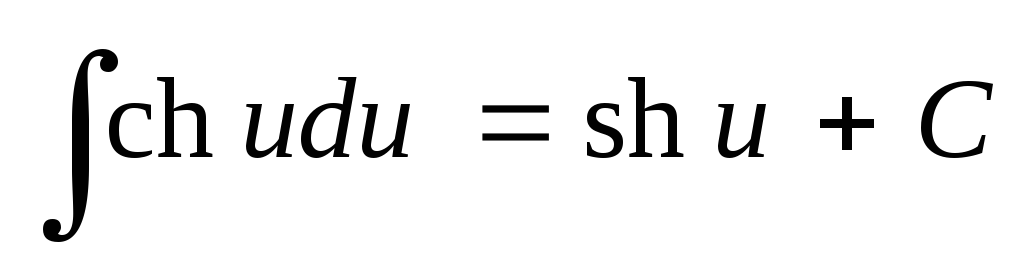 ;
;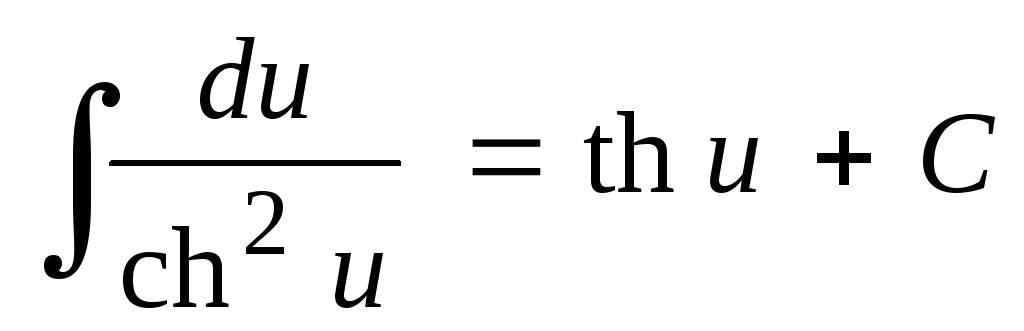 ;
;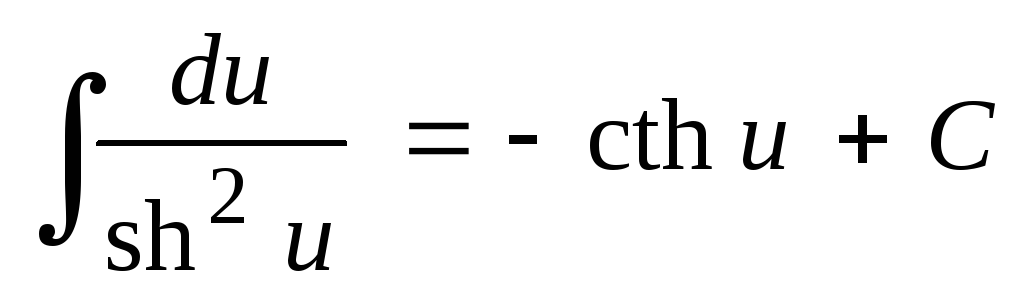 .
.
В
приведенной таблице u
может обозначать как независимую
переменную, так и непрерывно дифференцируемую
функцию
![]() аргументаx.
аргументаx.
2. Методы интегрирования Простейшие методы интегрирования
А). Метод разложения основан на разложении подынтегральной функции на сумму функций, каждая из которых является табличной (в частности, используя свойство 40).
Б).
Метод замены переменной состоит в
следующем. Вводится новая переменная
с помощью соотношения
![]() .
Тогда
.
Тогда![]() и исходный интеграл преобразуется
следующим образом
и исходный интеграл преобразуется
следующим образом
![]() ,
,
где
![]() - дифференцируемая функция. Затем
находится интеграл из правой части
(если это возможно) и осуществляется
возврат к исходной переменнойx,
используя соотношение
- дифференцируемая функция. Затем
находится интеграл из правой части
(если это возможно) и осуществляется
возврат к исходной переменнойx,
используя соотношение
![]() ,
полученное из соотношения
,
полученное из соотношения
![]() ,
выражаяt
через x.
При интегрировании некоторых функций
часто целесообразно осуществлять
переход к новой переменной с помощью
подстановки
,
выражаяt
через x.
При интегрировании некоторых функций
часто целесообразно осуществлять
переход к новой переменной с помощью
подстановки
![]() ,
а не
,
а не
![]() .
.
В).
Метод внесения функции под знак
дифференциала состоит в том, что новая
переменная не выписывается явно. Для
подынтегрального выражения выделяется
некоторая функция
![]() ,
дифференциал от которой
,
дифференциал от которой![]() входит составной частью в подынтегральное
выражением
входит составной частью в подынтегральное
выражением![]() ,
а оставшиеся часть является функцией
от
,
а оставшиеся часть является функцией
от![]() ,
т.е.
,
т.е.![]() .
Тогда исходный интеграл преобразуется
к виду:
.
Тогда исходный интеграл преобразуется
к виду:
![]()
Полученный интеграл может оказаться существенно проще, а в некоторых случаях свестись к табличным.
В заданиях 1 и 2 необходимо найти неопределенный интеграл, используя методы: разложения, замены переменной (или метод внесения функции под знак дифференциала) и таблицы неопределенных интегралов.
Задание 1. Найти неопределенные интегралы. Результат интегрирования проверить дифференцированием
a).
![]() , b).
, b).
![]() ,
,
c).
![]() , d).
, d).
![]() .
.
Решение: Для нахождения неопределенных интегралов можно воспользоваться как методом замены переменной, так и методом внесения под знак дифференциала. В первом случае, т.е. a), покажем оба метода. Остальные примеры будем решать только одним способом.
Задание
1 a).
![]() .
.
1.
Воспользуемся методом замены переменной.
Введем новую переменную t
по формуле
![]() .
Тогда
.
Тогда![]() или
или![]() .
Тогда
.
Тогда
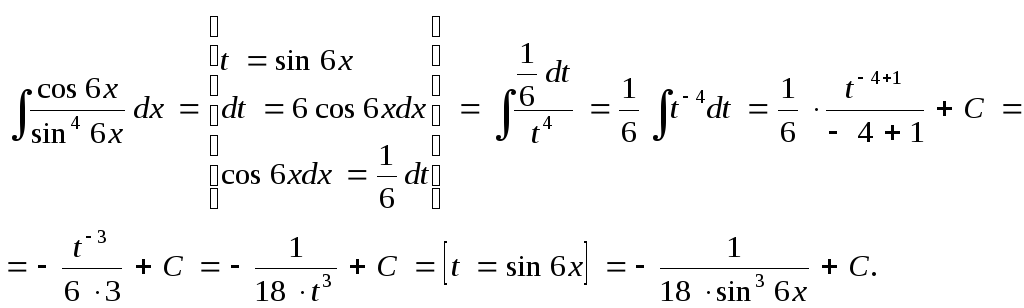
После
замены переменной воспользовались
свойством 40
неопределенного интеграла: постоянный
множитель
![]() можно выносить за знак неопределенного
интеграла, и так как
можно выносить за знак неопределенного
интеграла, и так как![]() ,
то пришли к табличному интегралу
,
то пришли к табличному интегралу![]() ,
где
,
где![]() и
и![]() .
.
2.
Решим этот пример методом внесения под
знак дифференциала. Замечая, что
![]() и то, что подынтегральное выражение
можно представить в виде
и то, что подынтегральное выражение
можно представить в виде
![]() ,
,
внесем
под знак дифференциала
![]() .
Для этого выпишем дифференциал этой
функции
.
Для этого выпишем дифференциал этой
функции![]() .
Тогда
.
Тогда
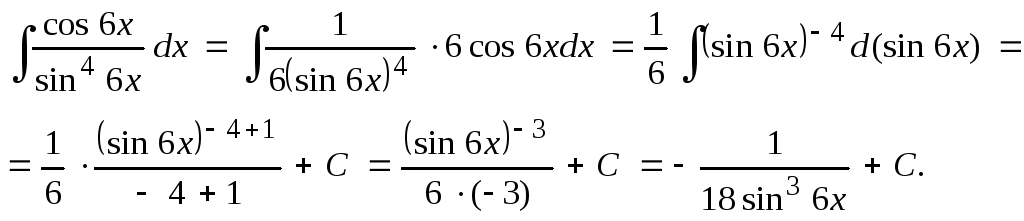
После
внесения под знак дифференциала функции
![]() пришли к табличному интегралу
пришли к табличному интегралу![]() ,
где
,
где![]() и
и![]() .
.
3. Результат интегрирования проверим дифференцированием. Для этого найдем производную
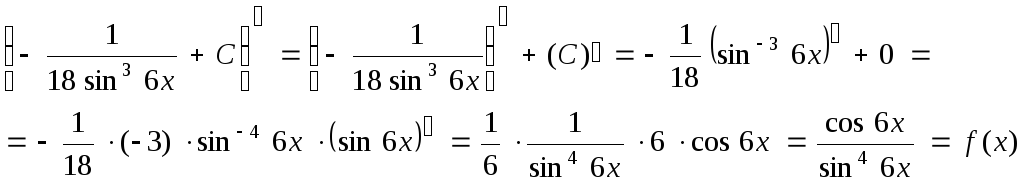
Таким образом, производная от неопределенного интеграла равна подынтегральной функции, то есть свойство 10неопределенного интеграла выполнено и, следовательно, интеграл от данной функции найден, верно.
Задание
1 b).
![]()
Воспользуемся
методом замены переменной. Введем новую
переменную t
по формуле
![]() .
Тогда
.
Тогда![]() или
или![]() .
Тогда
.
Тогда
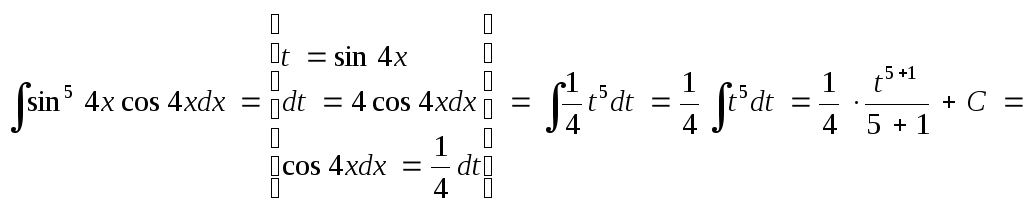
![]()
После
замены переменной воспользовались
свойством 40
неопределенного интеграла
![]() ,
и так как
,
и так как![]() ,
то пришли к табличному интегралу
,
то пришли к табличному интегралу![]() ,
где
,
где![]() .
.
Выполним проверку результата. Найдем производную
![]() .
.
Таким образом, производная от неопределенного интеграла равна подынтегральной функции.
Задание
1 c).
![]()
Воспользуемся
методом замены переменной. Введем новую
переменную t
по формуле
![]() .
Тогда
.
Тогда![]() или
или![]() .
Тогда
.
Тогда
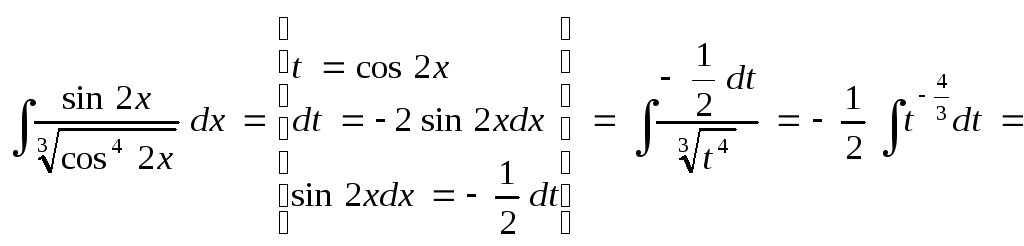
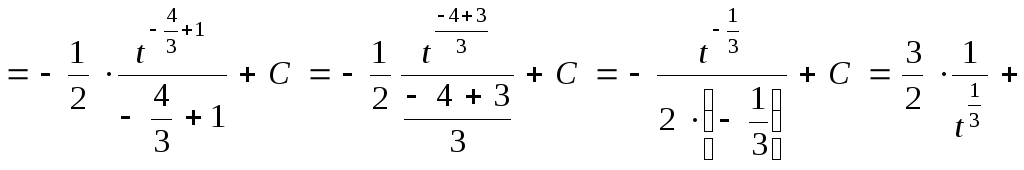
![]()
После
замены переменной воспользовались
свойством 40
неопределенного интеграла
![]() ,
и так как
,
и так как![]() ,
то пришли к табличному интегралу 1)
,
то пришли к табличному интегралу 1)![]() ,
где
,
где![]() .
.
Выполним проверку результата. Найдем производную
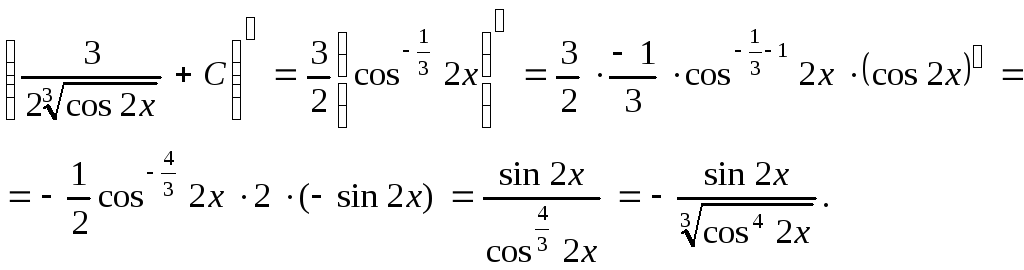
Таким образом, производная от неопределенного интеграла равна подынтегральной функции.
Задание
1 d).
![]()
Воспользуемся
методом внесения под знак дифференциала.
Внесем под знак дифференциала функцию
![]() .
Так как
.
Так как
![]() ,
,
то получим
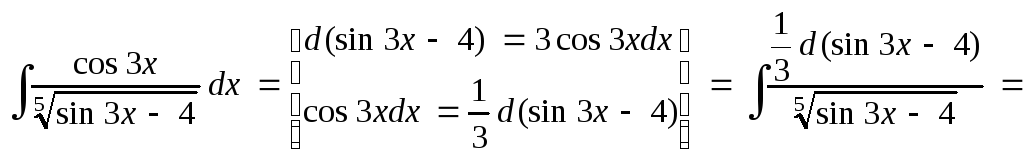
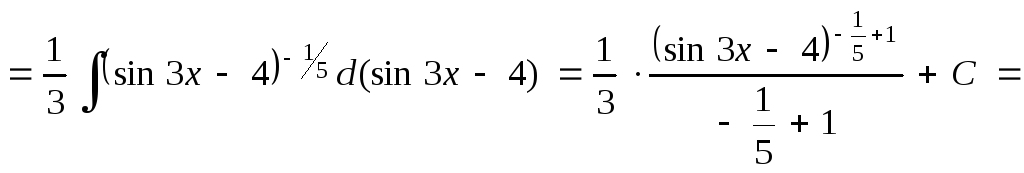
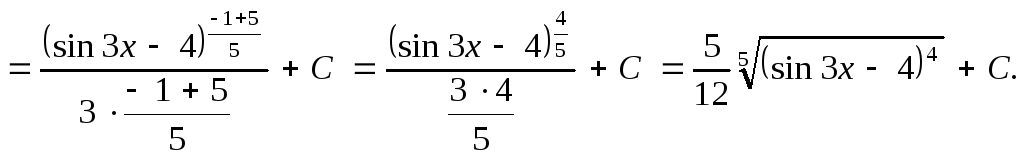
После внесения
под знак дифференциала функции
![]() пришли к табличному интегралу
пришли к табличному интегралу![]() ,
где
,
где![]() и
и![]() .
.
Выполним проверку результата. Найдем производную
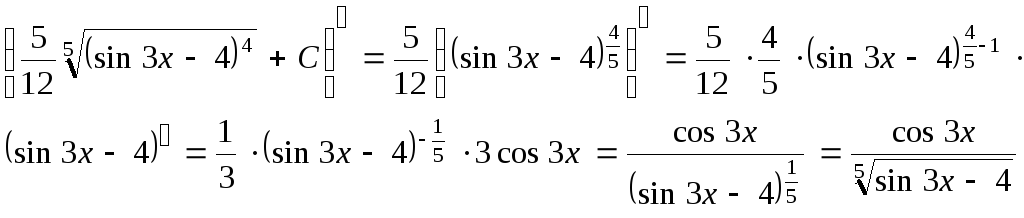
Таким образом, производная от неопределенного интеграла равна подынтегральной функции.
Задание 2. Найти неопределенный интеграл. Результат интегрирования проверить дифференцированием
a).
![]() ,b).
,b).
![]() , c).
, c).
![]() .
.
Решение: При выполнении задания 2 можно предварительно разбить подынтегральное выражение на сумму двух выражений и, применив свойство 50 неопределенных интегралов, получить два неопределенных интеграла. Как правило, один из них является табличным, а другой, используя метод замены переменной или метод внесения под знак дифференциала, к нему приводится.
Задание
2 a).
![]() .
.
Представим подынтегральную функцию в виде суммы двух дробей и, используя свойство 50, запишем интеграл в виде суммы двух интегралов. Для каждого из полученных интегралов применим метод внесения под знак дифференциала.
![]()
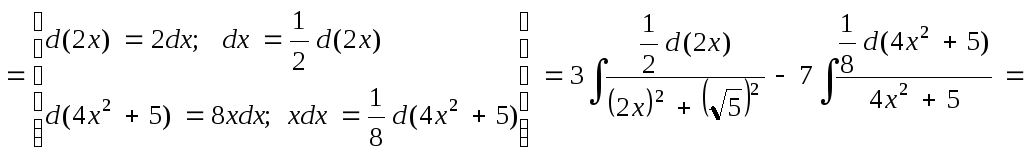
![]()
![]()
Приходим
к табличным интегралам: 9)
![]() ,
где
,
где
![]() ,
,
![]() и 2)
и 2)
![]() ,
где
,
где
![]() .
.
Выполним проверку результата. Найдем производную
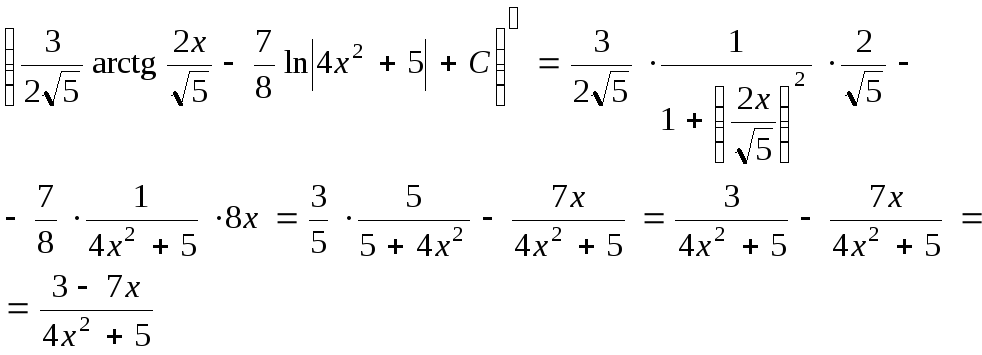
Таким образом, производная от неопределенного интеграла равна подынтегральной функции.
Задание
2 b).
![]() ,
,
Исходный
интеграл представляем в виде суммы двух
интегралов и, сделав замены переменных
![]() ,
придем к двум табличным интегралам:
,
придем к двум табличным интегралам:![]() ,
где
,
где![]() ,
,![]() и
и![]() ,
где
,
где![]() ,
,![]() .
Тогда
.
Тогда
![]()
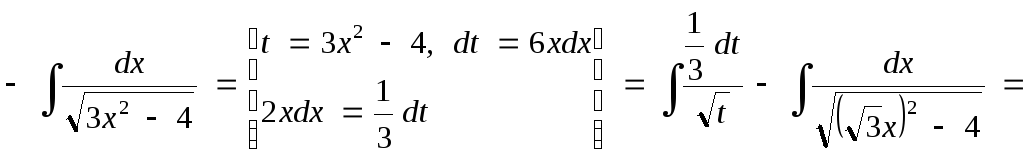
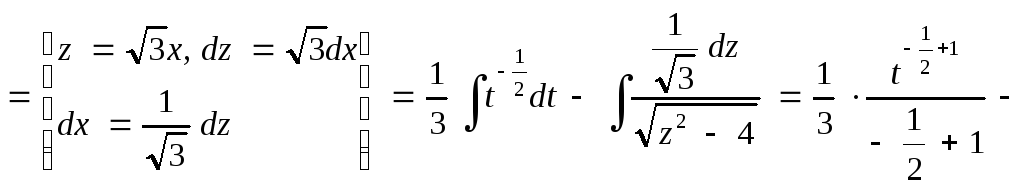
![]()
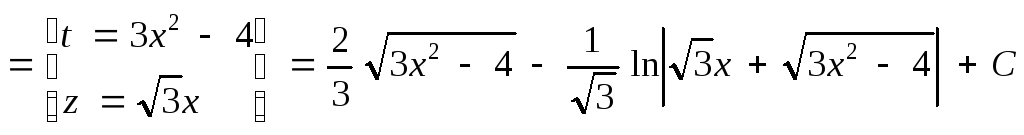
Выполним проверку результата. Найдем производную

Таким образом, производная от неопределенного интеграла равна подынтегральной функции.
Задание
2 c).
![]() .
.
Исходный
интеграл представляем в виде суммы двух
интегралов. Для первого интеграла, внеся
под знак дифференциала
![]() ,
получим табличный интеграл
,
получим табличный интеграл![]() ,
где
,
где![]() и
и![]() .
Второй интеграл является табличным
.
Второй интеграл является табличным![]() ,
где
,
где![]() и
и![]() .
.
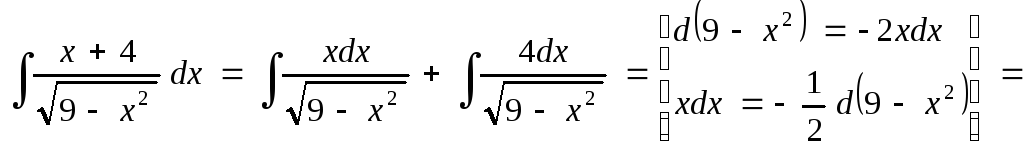
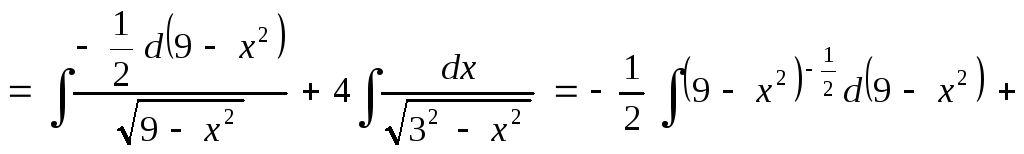
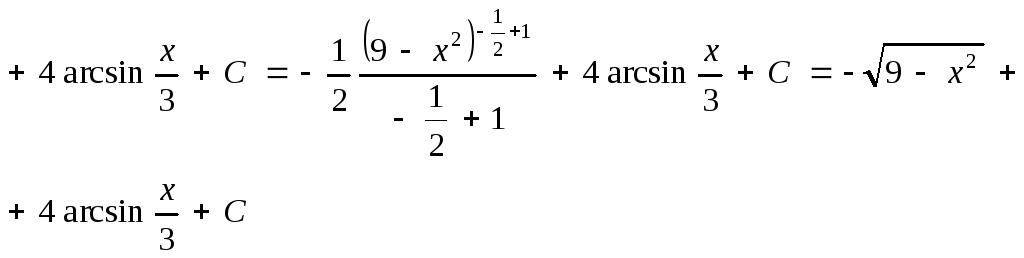
Выполним проверку результата. Найдем производную
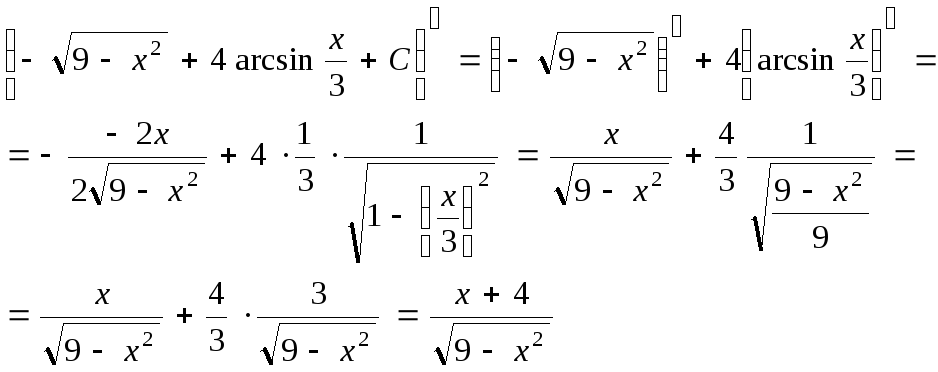
Таким образом, производная от неопределенного интеграла равна подынтегральной функции.
