2. З використанням вмонтованих функцій MathCad.

2.1. З використанням вмонтованих функцій Rkfixed(),Rcadapt() та Bulstoer().

Задаємо початкові умови у:=0, та в параметрах функції вказуємо початкові умови у, відрізок [0;1], кількість кроків інтегрування 10, раніше визначену функцію f.

2.2. З використанням вмонтованої функції Odesolve().

- початок обчислювального блоку

- диференційне рівняння

- початкові умови

- х – аргумент функції, 1 – кінець відрізка

інтегрування.

3. Розв’язок системи диференційних рівнянь за допомогою вмонтованих функцій.

3.1. За допомогою функції rkfixed().

Задаємо вектор-функцію, що містить праві частини диференційних рівнянь, в яких невідомі х(t) та у(t) представляємо у вигляді елементів деякого масиву невідомих х, причому невідома х(t) представлена як його елемент х0, а у(t) представлений як х1.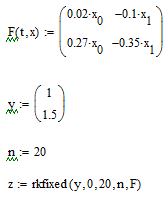

Викликаємо функцію, вказавши в списку параметрів вектор початкових умов у, відрізок інтегрування [0; 20], кількість кроків інтегрування n та вектор-функцію F(t,x). Результати отримуємо у вигляді масиву Z, де Zi,0 – номер точки і, Zi,1 – числові значення першої функції, Zi,2 – числові значення другої досліджуваної функції.

3.2. З використанням вмонтованої функції Odesolve().

Завдання №3

ІНТЕРПОЛЮВАННЯ ФУНКЦІЇ. АПРОКСИМАЦІЯ ЕКСПЕРИМЕНТАЛЬНИХ ДАНИХ . ЗАСОБИ НЕЛІНІЙНОЇ АПРОКСИМАЦІЇ. РОЗРАХУНОК ПАРАМЕТРІВ РІВНЯННЯ АНТУАНА

Завдання 1.

Побудувати інтерполяційний поліном Лагранжа, що повертає значення інтерполяційного многочлена в точках z та виконати лінійну інтерполяцію з використанням функції linterp(x,y,z).

Інтерполяція. Інтерполяційний поліном Лагранжа

Завдання 2.

1) Виконати лінійну та квадратичну апроксимації даних, визначивши значення параметрів a і b для рівняння функції у=f(x)=ax+b та a,b,c для рівняння функції у=f(x)=ax²+bх+с методом найменших квадратів, здійснити перевірку отриманих значень за допомогою вбудованих функцій:

slope(x,y), що повертає значення параметра a для таблично заданих x та y,

intercept(x,y), що повертає значення параметра b;

line(x,y), що повертає значення параметрів a і b;

regres(x,y,n), що визначає значення параметрів апроксимації табличної функції поліномом n-го порядку.

ЛІНІЙНА АПРОКСИМАЦІЯ

Визначення коефіцієнтів лінійної регресії методом найменших квадратів.

Квадратична апроксимація

Визначаємо похибку:

3) Виконати нелінійну апроксимацію даних, визначивши значення відповідних параметрів для:

1. рівняння Антуана за допомогою вбудованої функції genfit ;

2. експоненційної функції за допомогою вбудованої функції expfit;

3. логарифмічної функції за допомогою вбудованої функції logfit;

4. синусоїдальної функції за допомогою вбудованої функції sinfit;

5. степеневої функції за допомогою вбудованої функції pwrfit.

РОЗРАХУНОК ПАРАМЕТРІВ РІВНЯННЯ АНТУАНА

Рівняння Антуана має вигляд:

Розв'язок. Необхідно розрахувати значення параметрів a і b, які б максимально наближували дану функцію до вихідного масива даних.

1. Записуємо апроксимуючу функцію.

2. Знаходимо вирази для часткових похідних функції за шуканими параметрами (використовуємо символьний редактор).

3. Формуємо вектор початкових наближень.

4. Формуємо вектор-функцію F(x,z). x - незалежна змінна, z - вектор шуканих параметрів. В нашому випадку a=z₀, b=z₁, ^С= z₂. В нашому випадку вектор-функція буде мати 4 елементи – безпосередньо функція та три її часткових похідних..

5. Формуємо обчислювальну конструкцію, яка містить вбудовану функцію genfit та вказуємо всі необхідні аргументи цієї функції.

Результуючий вектор S містить в собі розраховані значення параметрів апроксимації. Представимо результати апроксимації графічно.

Перевизначення апроксимуючої функції з урахуванням знайдених параметрів

Порівнюємо отримані результати

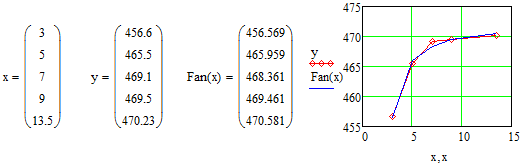
Визначаємо похибку апроксимації:

Представити результати апроксимації таблично і графічно разом з даними експерименту, проаналізувати похибки апроксимації.

Кількість вузлів інтерполяції:

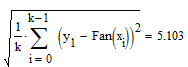
1. Експоненційна апроксимація

Апроксимація функцією виду y =

expfit(vx, vy, vz) -повертає вектор, що містить коефіцієнти а, b, c апроксимуючої функції вигляду y = , що найкращим чином описує дискретний набір точок, координати яких розміщені в векторах vx, vy. Вектор vz містить початкові наближення. Довжина вектора vz дорівнює кількості шуканих коефіцієнтів, тобто 3.

Знаходження коефіцієнтів регресії

Визначення апроксимуючої функції з урахуванням знайдених параметрів:

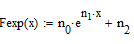
Порівнюємо отримані результати

Визначаємо похибку експоненціальної апроксимації:

ЗАВДАННЯ 4.

ПРОГРАМУВАННЯ В СИСТЕМІ MATHCAD.

1-й рівень складності (на «3») – задача обов’язкова: рішення системи лінійних алгебраїчних рівнянь (варіанти завдань обирати з табл.1) методом Зейделя.

Визначаємо вектор вільних членів beta та матрицю коефiцiєнтiв alfa за допомогою формул:

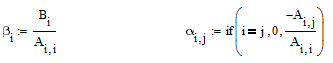
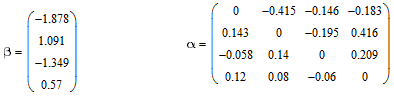
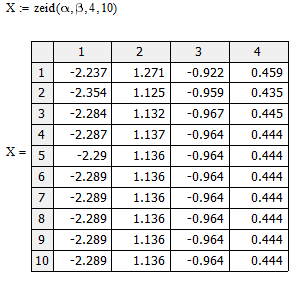
Метод Зейделя

alfa – матриця коефiцiєнтiв

beta – вектор вільних членів

n - кiлькiсть невiдомих

k – кiлькiсть iтерацiй

х – вектор рішень попередньої ітерації

у – вектор рішень поточної ітерації

1. 2-й рівень складності (на «4» на "5"): скласти програму з обробки двовимірного масиву (масиви значень взяти з попереднього завдання).

Транспортувати матрицю коефіцієнтів

ПОЧАТОК

і2,n,2

0

j2,m,2

кінець

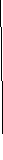
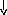
ІНТЕРПОЛЯЦІЯ НЬЮТОНА

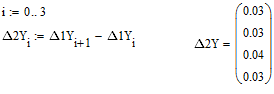
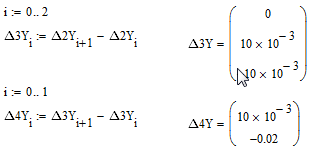
Висновок:

У курсовій роботі я розглянула лише першу формулу полінома Ньютона, яка працює поблизу початку таблиці. Інтерполяційний поліном у формі Ньютона зручно використовувати, якщо точка інтерполяції знаходиться поблизу початку таблиці. Цей поліном цікавий тим, що кожна часткова сума перших m доданків є інтерполяційний поліном m-1 ступеня, побудований за m перший табличним точкам. Тому інтерполяційні поліноми Ньютона зручно використовувати при послідовному збільшенні ступеня інтерполяційного многочлена.

До недоліку формули Ньютона можна віднести те, що при обчисленнях у таблиці з постійним кроком при збільшенні кількості вузлів не завжди вдається домогтися підвищення точності обчислень. Це обумовлено тим, що рівновіддалені вузли не є кращими з точки зору зменшення похибки інтерполювання. Якщо є можливості вибору вузлів інтерполяції, то їх слід вибирати так, щоб забезпечити мінімум похибки інтерполяції.

У процесі виконання курсової роботи були закріплені придбані за період навчання навички і вміння самостійного складання алгоритмів і програм на мові програмування Turbo Pascal 7.0 для вирішення простих типових математичних задач. Ця робота ще раз підтвердила корисність використання ЕОМ для вирішення прикладних математичних задач. Отримані знання і накопичений досвід вирішення простих завдань в майбутньому дозволять розробляти набагато більш складні програми і алгоритми, полегшать розбиття складних завдань на прості елементи.

45