
- •Варіанти контрольної роботи (студент виконує всі шість завдань, при цьому номер варіанта вказує викладач)
- •1. Вивчити основні властивості (алгебраїчність, асоціативність, комутативність, існування нейтрального елемента, наявність оборотних елементів) дії над елементами множини , якщо:
- •4. Знайти порядок елемента групи . Побудувати циклічну групу, породжену цим елементом та виписати усі її підгрупи:
- •5. Перевірити, чи утворює кільце щодо звичайних дій додавання та множення чисел множина . Якщо відповідь позитивна, то з’ясувати, чи є це кільце полем.
- •6. Перевірити, чи утворює кільце множина . Чи є це кільце полем?
Варіанти контрольної роботи (студент виконує всі шість завдань, при цьому номер варіанта вказує викладач)
1. Вивчити основні властивості (алгебраїчність, асоціативність, комутативність, існування нейтрального елемента, наявність оборотних елементів) дії над елементами множини , якщо:
|
№ варіанта |
|
|
№ варіанта |
|
|
|
1 |
|
|
11 |
|
|
|
2 |
|
|
12 |
|
|
|
3 |
|
|
13 |
|
|
|
4 |
|
|
14 |
|
|
|
5 |
|
|
15 |
|
|
|
6 |
|
|
16 |
|
|
|
7 |
|
|
17 |
|
|
|
8 |
|
|
18 |
|
|
|
9 |
|
|
19 |
|
|
|
10 |
|
|
20 |
|
|
2.
Яку алгебраїчну структуру (групоїд,
напівгрупу, моноїд чи групу) утворює
множина, задана у прикладі 1, щодо вказаної
дії
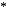 ?
?
3. Перевірити, чи буде групою задана множина щодо вказаної дії. Чи буде задана дія комутативною, якщо:
|
№ варіанта |
|
|
1 |
Множина всіх самосуміщень правильного многокутника відносно дії послідовного виконання перетворень. |
|
2 |
Множина
|
|
3 |
Множина
|
|
4 |
Множина
|
|
5 |
Множина
|
|
6 |
Множина
|
|
7 |
Множина
|
|
8 |
Множина
|
|
9 |
Множина
|
|
10 |
Множина
|
|
11 |
Множина
|
|
12 |
Множина
|
|
13 |
Множина
|
|
14 |
Множина всіх поворотів правильного многокутника відносно дії послідовного виконання поворотів. |
|
15 |
Множина
функцій
|
|
16 |
Множина
|
|
17 |
Множина
|
|
18 |
Множина
|
|
19 |
Множина
|
|
20 |
Множина
|


 ,
,
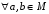
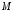
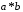 ,
,
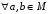
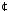
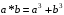
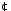
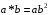

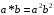

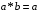
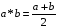
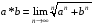
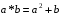
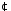
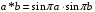
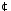
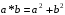
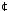
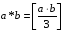
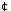
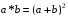

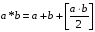
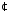
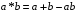
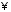
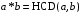
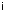
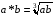
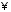
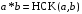
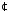

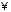
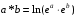
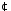

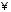
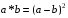
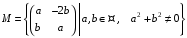 відносно дії множення
своїх елементів.
відносно дії множення
своїх елементів.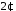 парних цілих чисел відносно дії
додавання.
парних цілих чисел відносно дії
додавання.
 всіх підстановок
всіх підстановок
 -го
степеня (
-го
степеня (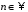 )
відносно дії множення
підстановок.
)
відносно дії множення
підстановок. всіх парних підстановок
всіх парних підстановок
 -го
степеня (
-го
степеня (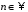 )
відносно дії множення підстановок.
)
відносно дії множення підстановок. всіх коренів
всіх коренів
 -го
степеня з одиниці (
-го
степеня з одиниці (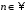 ,
,
 )
відносно дії множення своїх
елементів.
)
відносно дії множення своїх
елементів. цілих чисел, кратних
цілих чисел, кратних
 (
( ,
,
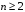 )
відносно дії додавання своїх
елементів.
)
відносно дії додавання своїх
елементів.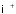 додатних дійсних чисел відносно дії
множення таких чисел.
додатних дійсних чисел відносно дії
множення таких чисел.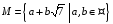 відносно дії додавання своїх
елементів.
відносно дії додавання своїх
елементів. відносно дії множення своїх елементів.
відносно дії множення своїх елементів.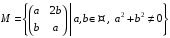 відносно дії множення своїх
елементів.
відносно дії множення своїх
елементів.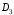 всіх самосуміщень правильного
трикутника відносно дії послідовного
виконання перетворень.
всіх самосуміщень правильного
трикутника відносно дії послідовного
виконання перетворень.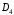 всіх самосуміщень квадрата відносно
дії послідовного виконання
перетворень.
всіх самосуміщень квадрата відносно
дії послідовного виконання
перетворень.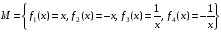 відносно дії суперпозиції функцій.
відносно дії суперпозиції функцій.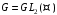 невироджених матриць другого порядку
з раціональними елементами щодо
дії множення матриць.
невироджених матриць другого порядку
з раціональними елементами щодо
дії множення матриць.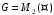 матриць другого порядку з раціональними
елементами щодо дії додавання
матриць.
матриць другого порядку з раціональними
елементами щодо дії додавання
матриць.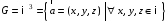 векторів простору щодо дії додавання
векторів.
векторів простору щодо дії додавання
векторів.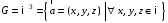 векторів простору щодо дії векторного
множення векторів.
векторів простору щодо дії векторного
множення векторів.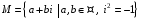 щодо дії множення своїх елементів.
щодо дії множення своїх елементів.