Симетричні многочлени від n змінних над числовим полем р

Усно

Серед многочленів від декількох змінних виділяють декілька з них, які не змінюються при жодній перестановці змінних. У такі многочлени всі змінні входять симетричним чином. Такі многочлени відіграють важливу роль у алгебрі.

Означення 7. Многочлен від n змінних над полем Р називаютьсиметричним, якщо він не змінюється при будь-якій перестановці змінних.

Приклад:

а) – симетрична

б) – не симетрична

Оскільки будь-яка підстановка дорівнює добутку транспозицій, то перевірка на симетричність довільного многочленна зводиться до перевірки того, що даний многочлен не змінюється при перестановці будь-яких двох його змінних.

Властивості:

а) всі многочлени нульового степеня є симетричними многочленами;

б) сума, різниця і добуток симетричних многочленів від n змінних є симетричним многочленом від цих змінних;

в) якщо – симетричний многочлен від, то–симетричний многочлен.

г) симетричні многочлени від змінних над Р утворює підкільце в кільцівсіх многочленів, яке називаютькільцем симетричних многочленів над полем Р.

Наступні n симетричних многочленів від n змінних називаються елементарними симетричними многочленами:

(1)

При n=2:

n=3:

Усно:

Ці многочлени, симетричність яких очевидна, відіграють в теорії симетричних многочленів дуже велику роль. Вони підказані формулами Вієта. А тому можна сказати, що коефіцієнт многочленна від однієї змінної, мають старший коефіцієнтом одиницю будуть, з точністю до знака, елементарними симетричними многочленами від його коренів.

Цей зв’язок елементарних симетричних множників з формулами Вієта буде досить суттєвим для тих застосувань симетричних многочленів до теорії множників від однієї змінної, заради яких ми їх вивчаємо.

Враховуючи властивості а) – г) маємо, що кожен многочлен від елементарних симетричний многочленів з коефіцієнтами з Р, якщо його розглядати як многочлен від буде симетричним.

Іншими словами, комбінація елементарних многочленів є симетричним многочленом.

Приклад:

Нехай n=3. Розглянемо

–симетричний многочлен від .

Оберненим до цього маємо наступне твердження:

Теорема 2 (основна теорема про симетричні многочлени):

Кожен симетричний многочлен від змінних над полем Р є многочленом від елементарних симетричних многочленів з коефіцієнтами із поля Р.

Іншими словами, будь-який симетричний многочлен однозначно виражається через елементарні симетричні многочлени.

Доведення.

Нехай задано симетричний многочлен

і нехай

(2)

– старший член цього многочленна. Показник при змінних ц цьому члені повинні задовольняти умову:

(3)

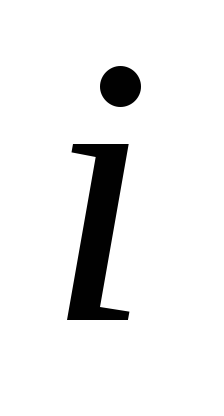
• Дійсно, якщо би при деякому 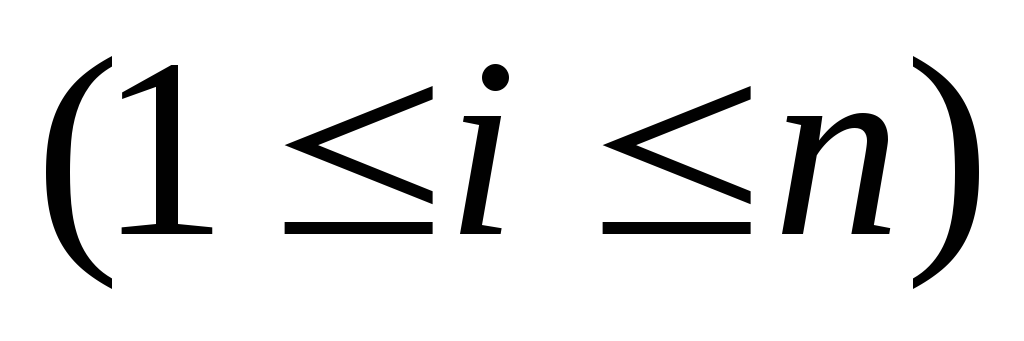було

Оскільки многочлен – симетричний, то він повинне містити член

(4)

який отримується із (2) транспозицією змінних та. Це приводить до протиріччя, оскільки член (4), у сенсі лексикографічного запису, вище члена (2):

показники при в обох членах рівні, але показник приу (4) більше, ніж у члені (2).

Розглянемо тепер наступний добуток елементарних симетричних многочленів (в силу нерівності (3), всі показники – невід’ємні).

(5)

Це буде симетричний многочлен від змінних .

• Покажемо, що члени многочленів рівні відповідно

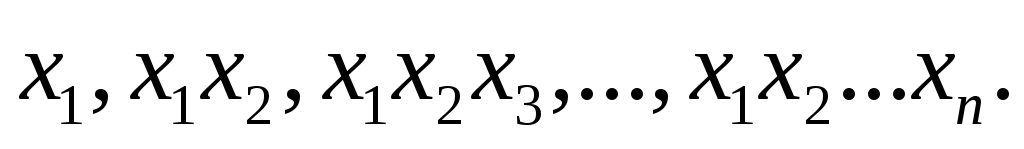
Згідно з теоремою 1, вищий член многочленна має вигляд:

Отже, якщо розглянути многочлен то старий членнижче старшого члена(бо ст. чл.= ст. чл.)

Повторюючи для многочленна аналогічні побудови (коефіцієнти якого належать полю Р), отримуємо многочлен.

де – добуток степенів елементарних симетричних многочленів, з деяким коефіцієнтом із поля Р, а–симетричний многочлен, вищий член якого нижче, ніж вищий член в.

Звідси отримуємо:

Продовжуючи цей процес, для деякого отримаємо.

Таким чином, отримуємо вираження через многочлен від з коефіцієнтами із поля Р:

• Покажемо, що цей процес є скінченним.

Припустимо, що цей процес –нескінченний. Тоді отримуємо нескінченну послідовність симетричних многочленів

(6)

причому вищий член кожного із них є нижчим, ніж вищі члени попередніх многочленів і, тим більше, нижчий ніж (2).

Однак, якщо в

(7)

є вищий член многочленна , то із симетричності цього многочленнанерівність:

(8)

аналогічно до (3). З іншого боку, оскільки член (2) вище члена (7), то

(9)

Але не складно зрозуміти, що системи цілих невід’ємних чисел , що задовольняє нерівності (8) та (9), можна вибрати тільки скінченною кількістю способів., що послідовність многочленів (6) зі строго понижающимися вищими членами, не може бети нескінченним.

Теорему доведено.

Наслідок. Нехай – многочлен від однієї змінної над полем Р,(старший коефіцієнт = 1).

Тоді кожен симетричний многочлен (з коефіцієнтами із Р) від коренів многочленна буде многочленом від коефіцієнтів многочлена.

Теорема 3. (теорема єдиності)

Кожен симетричний многочлен має єдине вираження у вигляді многочленів від елементарних симетричних многочленів.

Дов. – Курош, ст. 219-220.

Симетричні многочлени мають широке використання в алгебрі:

а) при розв’язуванні деяких системних рівнянь;

б) при розв’язуванні деяких ірраціональних рівнянь;

в) при знищенні ірраціональності у знаменнику;

г) при обчисленні наближення значень коренів та інші.

Наприклад, розв’язати систему рівнянь:

Маємо систему:

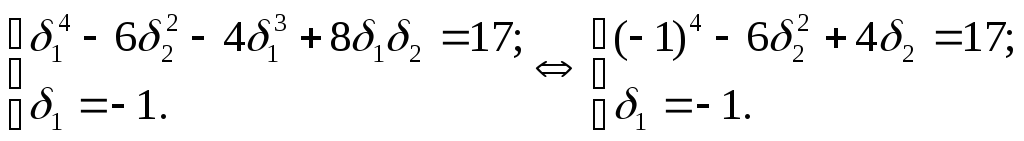
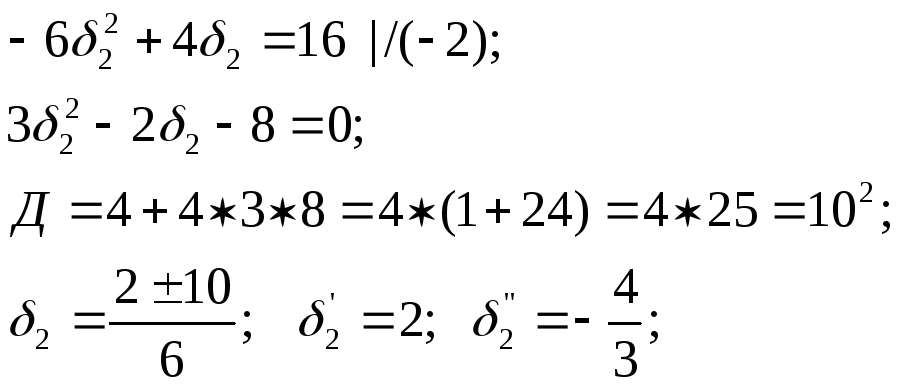
Маємо:

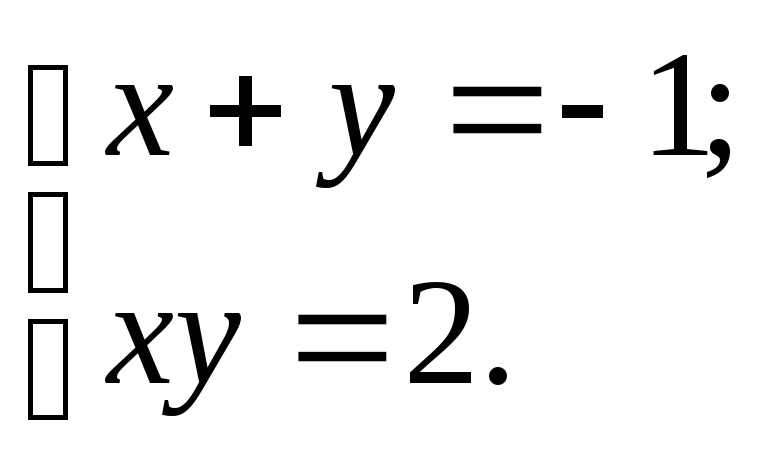або

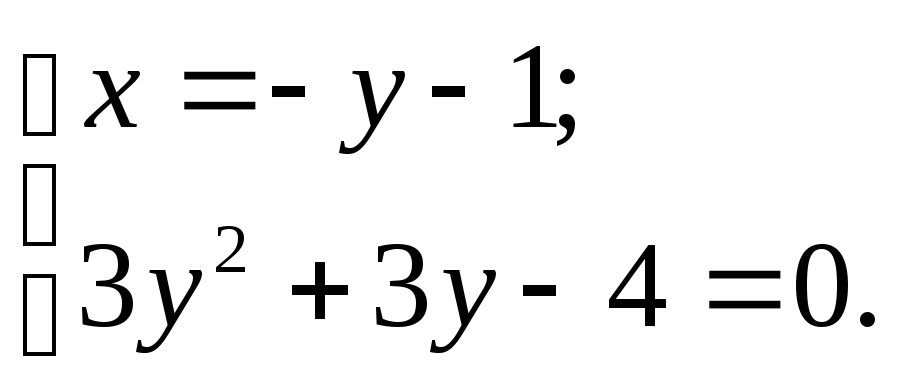
Д=57;