Многочлени від декількох змінних

Часто в математиці потрібно розглядати многочлени, які залежать не від однієї, а від двох, трьох, взагалі кажучи, від декількох змінних.

Нехай – n змінних(або n невідомих),– числа.

Означення 1. Вираз , де, а –елемент поля р, називають одночленом від змінних.

Суму називають степенем одночлена.

Розглянемо ще один одночлен:

Означення 2. Два одночлена називаються рівними, якщо:

Два одночлена називаються подібними, якщо:

Означення 3. Многочлен від багатьох змінних над полем Р (тобто є коефіцієнтом з поля Р) називається сума скінченої кількості одночленів.

Наприклад:

Означення 4. Степенем многочленна (за сукупністю змінних) називається найбільший із степенів його одночленів (членів).

Для прикладу:

І дод. степеня 5+1+0=6 степінь многочленна

ІІ дод. степеня 2+4+1=7 =8

ІІІ дод. степеня 0+2+6=8

Означення 5. Степенем многочленна відносно змінної називається показник, з якимвходить в члени цього многочленна.

Приклад: – найвищий степінь = 5;

–найвищий степінь = 4;

–найвищий степінь = 6.

Означення 6. Два многочленна від змінних з коефіцієнтами з одного і того ж поля Р називається рівними, якщо вони складаються з одних і тих же членів (може відрізнятися тільки порядком запису членів).

У протилежному випадку – многочлени не рівні.

Одним із многочленів від n змінних є многочлен нульового степеня і нульовий многочлен.

Дії над многочленами

1. Додавання

При додаванні двох многочленів і, до членів одного многочленна дописують члени іншого і зводимо подібні члени (одночлени). При цьому:

2. Множення

Добутком двох многочленів іназивається многочлен від змінних, який отримається, коли члени одного многочленна і звести подібні члени.

При цьому:

Добутком двох ненульових многочленів є ненульовий многочлен степінь якого дорівнює сумі степенів множників (по сукупності змінних).

Властивості дій:

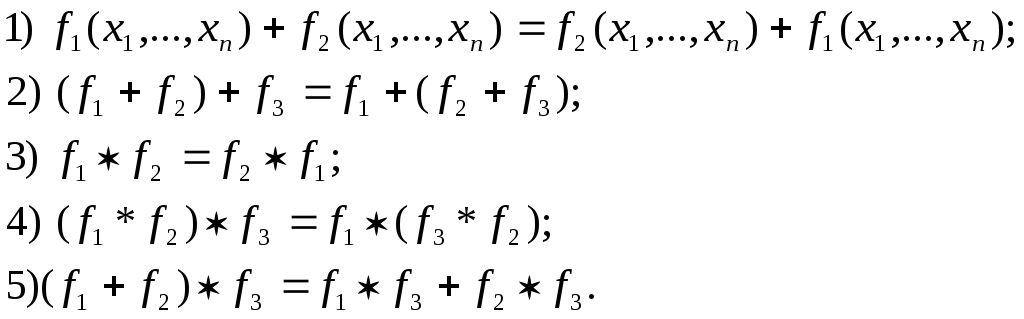
Для додавання існує обернена дія – віднімання. Це означає, що рівняння

однозначно розв’язується для будь-яких многочленів :

Зауваження: Многочлени від декількох змінних над полем Р утворюють кільце, яке називають кільцем многочленів і позначають .

Лексикографічний запис многочленна

Ми знаємо, що для многочленна від однієї змінної , користуються записом членів за спадними або за зростаючими степенями.

У випадку многочленна від декількох змінних такі способи вже відсутні. Але є так званий лексикографічний запис.

Нехай задано многочлен .

Спочатку порівняємо у всіх членах степені відносно змінної . Вибираємо член, у якомуу найвищому степені і записуємо його на І місце.

Якщо є кілька членів, де у найвищому степені, то порівняємо степені при. Вищим буде той член, у якому вищий показник змінноїі т.д.

Таке порівняння і такий порядок запису називають лексикографічним записом многочленна.

Член, який у лексикографічному записі могочлена стоїть на першому місці називають вищим (найвищим) членом многочленна.

Приклад:

–лексикографічний запис многочленна.

Має місце важливе твердження:

Теорема 1. Вищий (найвищий) член добутку двох многочленів від декількох змінних дорівнює добутку їх вищих членів.

(дов. див. у Куроша, ст. 213)