Власні значення і власні вектори лінійного оператора.

Характеристична матриця, поліном, корені.

Розглянемо квадратичну матрицю

Ми знаємо, що кожна квадратна матриця відповідає деякому лінійному оператору в даному базисі.

Означення 1: Матрицю

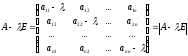
називається характеристичними поліномом (або многочленів) для матриці А.

Після обчислення визначника

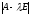
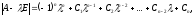де

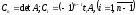
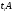­– сума головного мінорів і-го порядку.

Означення 2: Визначник характеристичної матриці 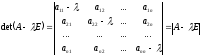називається характеристичним поліномом (або многочленом) для матриці А.

Після обчислення визначника

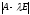
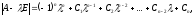де

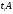­– сума головного мінорів і-го порядку.

Наприклад:

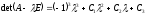
Характеристичний поліном матриці А п-го порядку є поліномом п-го степеня. Отже, він має п коренів:

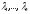
Означення 3: Корені характеристичного полінома називається характеристичними коренями матриці А.

Означення 4: Характеристичними коренями лінійного оператора називається характеристичні корені його матриці.

Приклад:

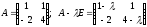
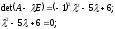
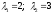–характеристичні корені А.

Зауваження 1: Якщо матриця А діагональна, то характеристичними коренями матриці А є її діагональні елементи.

Зауваження 2: Характеристичні многочлени подібних матриць – однакові.

Дов. Дійсно, В~А 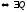–невироджена, що

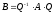
Розглянемо

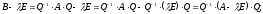
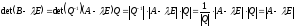
Що і треба було довести.

Власні вектори лінійного оператора.

Означення 5: Ненульовий вектор в називається власним вектором лінійного оператора 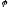,якщо образ 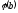пропорційний цьому вектору, тобто:

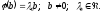
Число називаєтьсявласним значенням лінійного оператора , яке відповідає власному векторув.

Приклад: – лінійний простір простору.

­ – ортогональне проектування векторів на деяку площину .

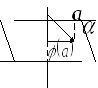
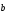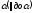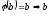а) Якщо належить площині, то– власний вектор з власними значеннями.

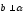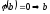б) Якщо , то– власний вектор, який відповідає.

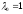Теорема 1: (про зв’язок характеристичних коренів лінійного оператора його власними значеннями).

Дійсні характеристичні корені лінійного оператора простору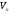і тільки вони є власними значеннями цього оператора.

Дов. Необхідність.

Нехай – власне значення, лінійного оператора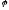. Доведемо, що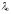, тобто:

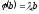(1)

Розглянемо деяку базу

в просторі 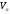. Нехай в цій базі оператора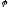 має матрицю ;

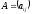Підставимо ці вирази в (1). Враховуючи, що

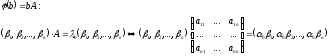
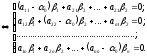(2)

(2) – це однорідна система рівнянь. Вектор 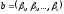– ненульовий, тому система (2), як однорідна , має визначник, рівний нулю:

(3)

У протилежному випадку, якщо визначник системи був відмінний від нуля, то система (2) мали би нульовий 1 розв’язок.

Але, за умовою, – ненульовий розв’язок.

Транспонований визначник (3):

(4)

(4)- характеристичне рівняння для матриці А, отже, - характеристичний корінь матриці А.

Достатність.

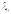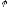Нехай дійсний характеристичний корінь лінійного оператора. Треба довести, що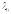є власним значення лінійного оператора.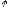

Це означає, що однорідна система (2) ненульовий розв’язок .

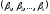Отже, має місце (2) і (1).

А рівність (1) означає, що вектор 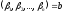є власним вектором оператора, який відповідає власному значенню.

Теорему доведено.

Приклад: Знайти власні вектори оператора 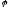, який задається матрицею

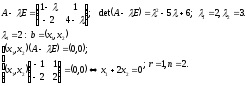
або

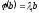
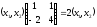
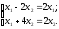
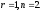
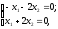
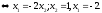
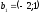–відповідають власні значення .

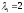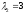
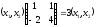
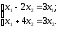
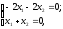
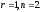
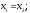
– власний вектор, що відповідає власному значенню

Зауваження:

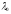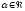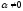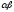1) Якщо власний вектор, що відповідає власному значенню , то для довільного,,– теж власний вектор, що відповідає.

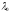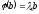–дано;

.

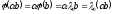2) Якщо 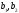– власні вектори, що відповідають власним значенням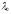, то

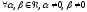
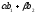–власний вектор, що відповідає .

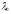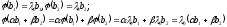
Теорема: Власні вектори, що відповідають, що відповідає лінійний оператор , котрі відносяться до різних власних значень, лінійно незалежні.

(без доведення)

Лінійні оператори з простим спектром.

Означення 6: Множина характеристичних коренів лінійного оператора називається спектром цього оператора.

Означення 7: Спектр називається простим, якщо всі характеристичні корені дійсні та різні.

Теорема 3: Матриця лінійного оператора буде діагональною в базітоді й тільки тоді, коли ця база ця база буде складатися з власних векторів оператора.

Дов. Необхідність

Нехай оператор задається діагональною матрицею А в базі 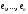, тобто

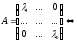
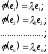
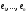–власні вектори оператора .

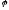Достатність

Нехай 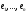– власні вектори оператора. Треба довести, що матриця А діагональна.

Згідно з умовою,

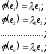
Тоді в базі 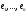матриця оператора має вигляд:

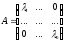
Теорема 4: Для лінійних операторів з простим спектром завжди існує база, в якій матриця оператора діагональна.

Довести самостійно.

Нехай 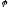– лінійний оператор з простим спектром. Тобто характеристичні корені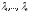– дійсні, різні.

Довести, що база, в якій матриця цього оператора має діагональну форму.

Якщо 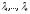– власні значення оператора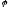, то нехай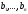– власні вектори оператора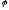, що відповідають цим значенням:

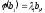
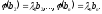
Власні вектори 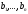відносяться до різних власних значень, тому (за теоремою), вони лінійно незалежні.

Оскільки їх кількість = розмірності простору, то можемо їх вибрати за базу простору

В цьому базисі оператор має матрицю

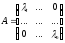–діагональна.

А база – існує завжди.

Теорему доведено.

55