- •Лінійний простір. Аксіоматика. Ізоморфізм.
- •Скінченновимірні лінійні простори. Базис. Розмірність простору. Перетворення базису.
- •Підпростори лінійного простору. Їх сума та перетин.
- •Перетин (переріз) лінійних підпросторів.
- •Сума підпросторів лінійного простору.
- •Теорема про зв’язок між розмінностями суми і перерізу лінійних підпросторів.
- •Лінійні оператори. Їх властивості
- •Область значень та ядро лінійного оператора.
- •Власні значення і власні вектори лінійного оператора.
Підпростори лінійного простору. Їх сума та перетин.
Означення лінійного простору.
Нехай
задано лінійний просторі
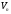 . розглянемо не порожню підмножину
. розглянемо не порожню підмножину елементів простору
елементів простору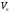 .
.
Означення
1.
підмножина
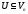 називаєтьсялінійним
підпростором лінійного
простору
називаєтьсялінійним
підпростором лінійного
простору
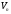 ,
якщо:
,
якщо:
1)
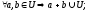
2)
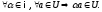
Оскільки
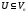 ,
то всі аксіоми лінійного простору дляU
будуть виконуватись.
,
то всі аксіоми лінійного простору дляU
будуть виконуватись.
Приклади підпросторів:
1.
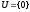 – містить лише нульові елементи із
– містить лише нульові елементи із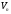 ;
;
 –весь
простір.
–весь
простір.
– це приклади тривіальних підпросторів.
2.
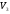 – лінійний простір геометричних векторів
із
– лінійний простір геометричних векторів
із .
.
U – множина векторів, що лежать у деякій площині, котра проходить через початок координат.
3.
 – множина лінійного простіру матрицьп-го
порядку з дійсними елементами.
– множина лінійного простіру матрицьп-го
порядку з дійсними елементами.
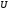 –множина
всіх симетричних матриць п-го
порядку є дійсними елементами – є
підпростором.
–множина
всіх симетричних матриць п-го
порядку є дійсними елементами – є
підпростором.
А
симетр.
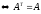
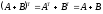 –
симетр.
–
симетр.
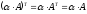 –симетр.
–симетр.
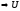 – лінійний простір.
– лінійний простір.
Зауваження:
Оскільки простір
 сам є лінійним простором, то для нього
модна вводити аналогічні поняття бази
і розмірності.
сам є лінійним простором, то для нього
модна вводити аналогічні поняття бази
і розмірності.
Очевидно, що підпростір U п-вимірного простору є скінченновимірним, бо його база не може містити векторів більше, ніж в базі самого простору. Отже,
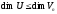
Перетин (переріз) лінійних підпросторів.
Твердження
1. Перетин
лінійних підпросторів простору
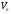 є
також лінійним підпростором у
є
також лінійним підпростором у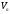 .
.
Тобто,
якщо
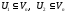 – лінійні підпростори, то
– лінійні підпростори, то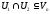
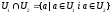
(доведення самостійно) – випливає з озн. підпростору і перетину множини.
Виникає
питання:
як можна будувати підпростори, їх
перетин, маючи елементи даного простору
 .
.
Розглянемо систему векторів
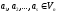 і
розглянемо все можливі лінійні комбінації
цих векторів:
і
розглянемо все можливі лінійні комбінації
цих векторів:
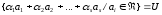 (1)
(1)
Твердження 2: Так побудована множина
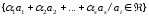 є
підпростором простору
є
підпростором простору
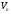 .
.
Дов.
Нехай

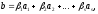
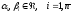
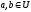 ,
тому
,
тому
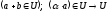 –підпростір.
–підпростір.
Множина
вигляду (1) називається лінійною
оболонкою векторів
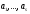 і
позначають
і
позначають
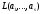 або
або
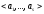
Отже,
(2)
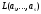 =
=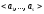 =
=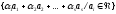
Неважко перевірити, що
(3)
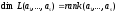
Зауваження:
Якщо
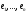 – база простору
– база простору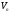 ,
то
,
то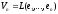
Сума підпросторів лінійного простору.
Нехай
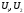 – підпростори лінійного простору
– підпростори лінійного простору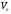 .
.
Означення
2:
Сумою
підпросторів
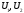 називається така множина
називається така множина

яка
складається з тих векторів із
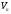 ,
які хоча б одним способом можна зобразити
у вигляді суми одного вектора з
,
які хоча б одним способом можна зобразити
у вигляді суми одного вектора з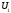 ,
а іншого –з з
,
а іншого –з з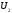 .
.
(4) 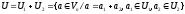
Приклад:
Нехай
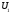 – вектори, що лежать на
– вектори, що лежать на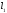 ,
,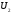 – вектори, що лежать на
– вектори, що лежать на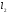 ;
;
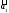

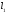
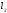
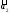

Очевидно,
що
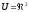
Зауваження:
Підпростори
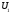 і
і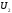 містяться в підпросторі
містяться в підпросторі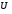 :
:
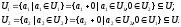
Твердження
3. Сума
підпросторів
 і
і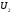 є підпростором простору
є підпростором простору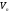 :
якщо
:
якщо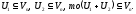
Дов.
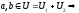

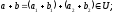
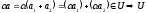 –підпростір.
–підпростір.
Зауваження: можна ввести, за індукцією, суму (перетин) довільної кількості лінійних підпросторів.
Теорема про зв’язок між розмінностями суми і перерізу лінійних підпросторів.
Теорема:
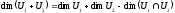
Дов. Введемо позначення:
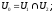
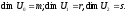
Тоді
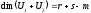 – доведемо.
– доведемо.
Нехай
 – база простору
– база простору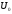 (1)
(1)
Її можна доповнити векторами.
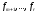 з
з
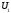 так,
щоб отримати базу простору
так,
щоб отримати базу простору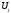 .
.
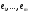 ,
,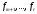 – база
– база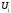 (2)
(2)
(оскільки
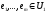 і
і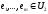 ,
бо належать їх перетину)
,
бо належать їх перетину)
Аналогічно,
доповнимо систему (1) до бази простору
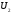 :
:
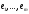 ,
,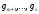 (3)
(3)
Розглянемо систему векторів:
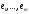 ,
,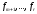 ,
,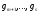 (4)
(4)
Виникає
питання: чи буде (4) базою в
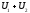 (бо в ній є векторів рівно
(бо в ній є векторів рівно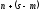 )
)
Для доведення теореми потрібно довести два фактори:
система (4) – лінійно залежна;
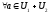 треба
показати, що а
лінійно
виражається через (4).
треба
показати, що а
лінійно
виражається через (4).
Доводимо це:
1)
Розглянемо лінійну комбінацію векторів
системи (4):
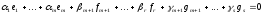 (5)
(5)
Потрібно
переконатися, що
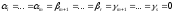
Перепишемо (5) ц іншому вигляді:

З
останньої рівності
 , що
, що .
Отже, його можна зобразити як лінійну
комбінацію векторів із
.
Отже, його можна зобразити як лінійну
комбінацію векторів із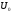 :
:
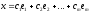
Отже,
 =
=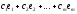
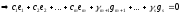
Оскільки система (3) лінійно незалежна, тоді маємо:
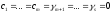
Із (5) тоді маємо:
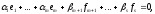
але (2) – теж лінійно незалежна, тому:
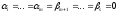
Отже, система (4) – лінійно незалежна.
2)
 – чи це так?
– чи це так?
Розглянемо вектори
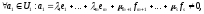
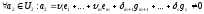
Обчислимо:
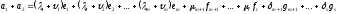
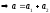 лінійно
виражається через систему (4) в
лінійно
виражається через систему (4) в
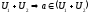
Отже
(4) – база простори
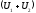
Тобто, в ній міст. в-в:
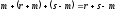 векторів
векторів