Приклади розв’язування задач Лінійні простори

1. Довести, що множина всіх многочленів степеня не вище 3 з дійсними коефіцієнтами, для яких , утворює дійсний лінійний простір. Вказати приклад бази та розмірність цього простору.

Розв’язок

Нехай — задана множина.

Перевіримо, чи виконуються аксіоми лінійного простору.

1)

,

,

.

та

2)

3) — виконується властивість додавання многочленів;

4) — виконується властивість додавання многочленів;

5)

—многочлен степеня з дійсними коефіцієнтами та.

6)

, бо

7)

— виконується !

8)

— виконується !

9)

— виконується!

10) — виконується !

(аксіоми 3,4,7-10 — це відповідні властивості многочленів довільного степеня від х, тому вони виконуються завжди — це доводили раніше в теорії многочленів).

Отже, —дійсний лінійний простір.

Приклад бази: .

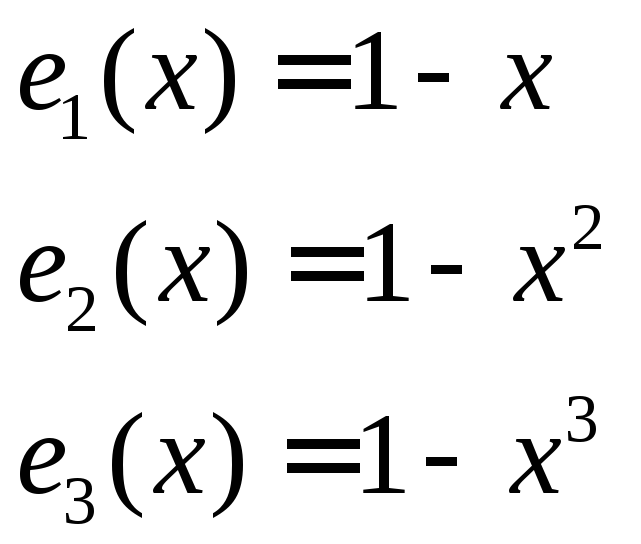
— розмірність цього простору.

2. Довести, що сукупність усіх векторів-рядків довжини 5, у яких друга координата у три рази більша за останню, утворює дійсний лінійний простір. Знайти деякий базис та координати вектора у вибраному базисі.

Розв’язок

Оскільки кожен елемент має другу координату у 3 рази більшу за останню, то можемо його подавати у вигляді:— довільні.

Перевіряємо тепер аксіоми лінійного простору:

1)

бо ІІ координата у 3 рази більша за останню.

2)

бо друга координата у 3 рази більша за останню.

3)

бо , бо друга координата у 3 рази більша за останню.

4)

5)

6)

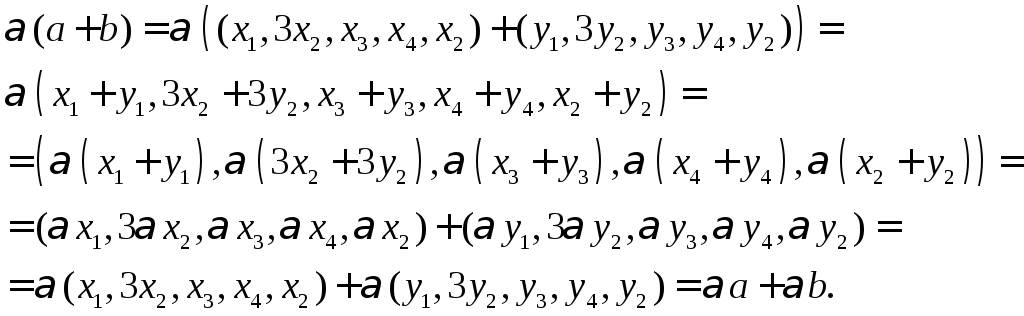
7)

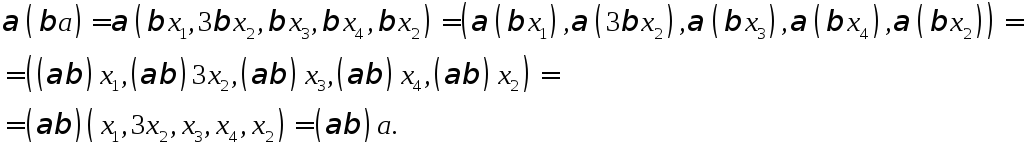
8)

9) — виконується для довільних-вимірних векторів, тому виконується і в даному випадку.

10) — асоціативність теж виконується для довільних-вимірних векторів.

Отже, — дійсний лінійний простір.

Базис:

Знайдемо координати вектора у цьому базисі.

—координати вектора у базисі.

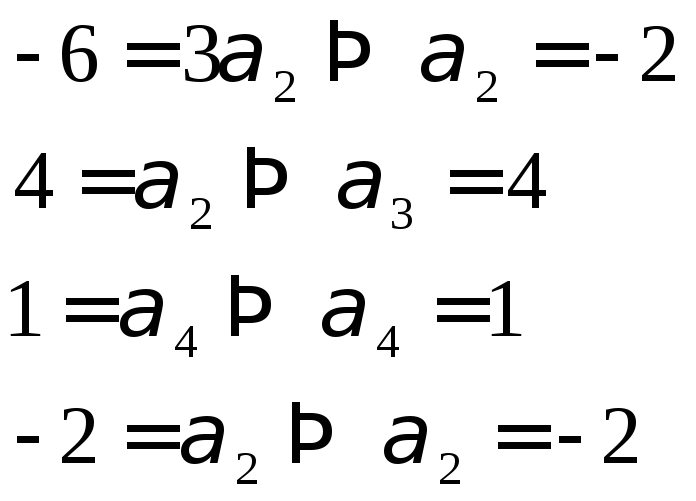
Отже — координати векторау базисі

3. Довести, що множина матриць третього порядку, симетричних відносно обох діагоналей з дійсними елементами, утворює дійсний лінійний простір. Знайти довільний базис і розмірність цього простору.

Розв’язок

Позначимо

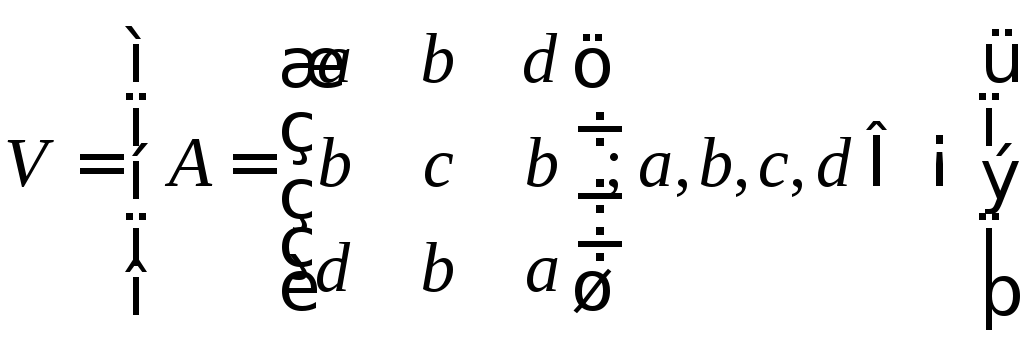— множина матриць 3-го порядку з дійсними елементами, симетричних відносно обох діагоналей.

Доведемо, що — лінійний простір.

Розглянемо 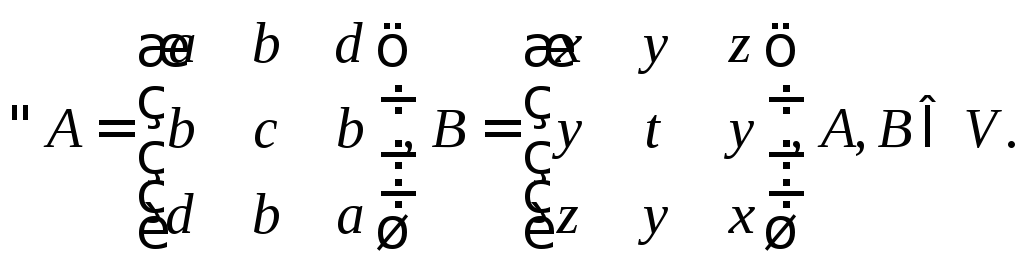Перевіримо аксіоми лінійного простору.

1) 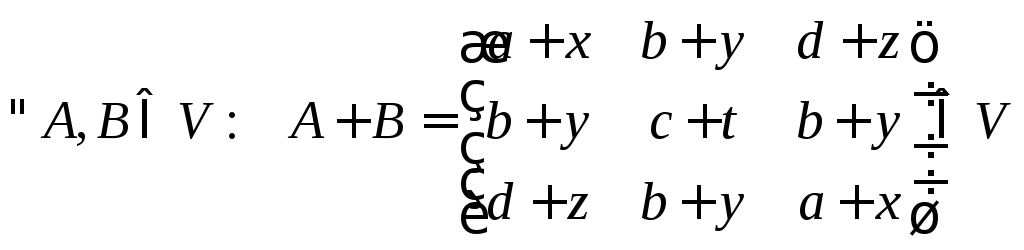— симетрична відносно обох діагоналей!

2)

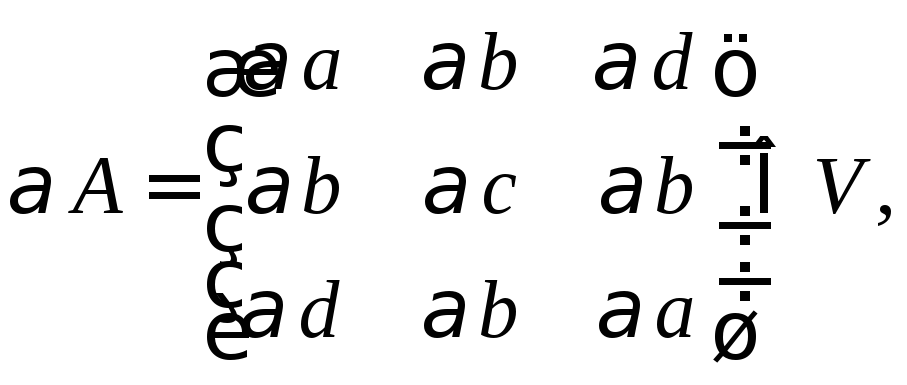бо матриця — симетрична відносно обох діагоналей.

3) — виконується (з І семестру знаємо!)

4) — виконується.

5) 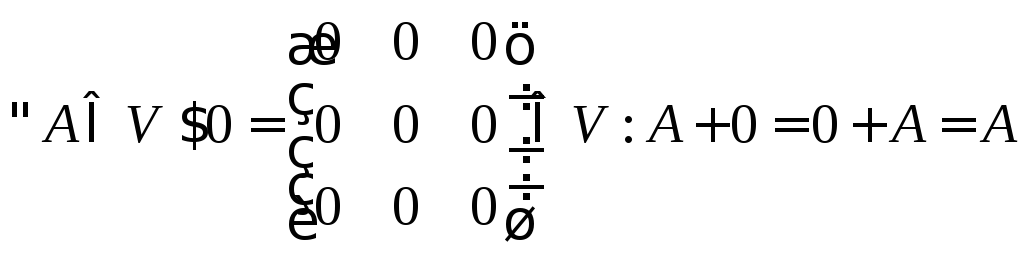— виконується!

6) — виконується!

7) — виконується!

8) — виконується!

9) — виконується!

10) — виконується!

Аксіоми 3) -10) — виконуються для довільних матриць 3-го порядку з дійсними елементами (І семестр, теорія матриць), тому вони виконуються і для симетричних відносно обох діагоналей матриць.

Отже, — дійсний лінійний простір.

Базис:

4. У дійсному лінійному просторі многочленів степеня не вище 3 знайти матрицю переходу від базису до базису

Розв’язок

Позначимо: 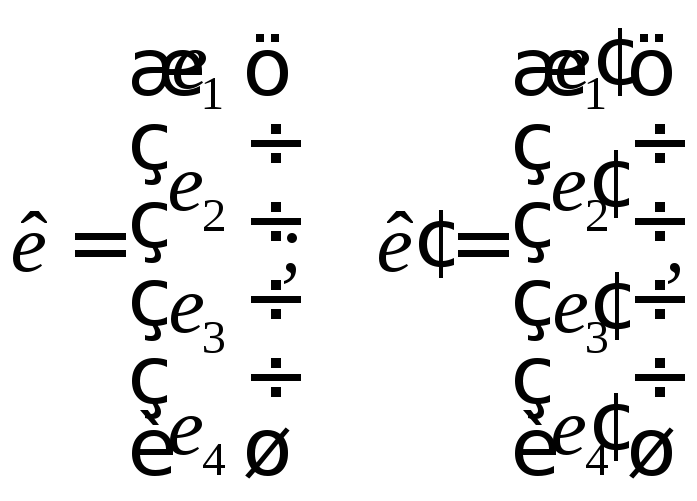тоді, де— шукана матриця переходу від базидо бази.

Вона складається з коефіцієнтів розкладу по базису,

Отже

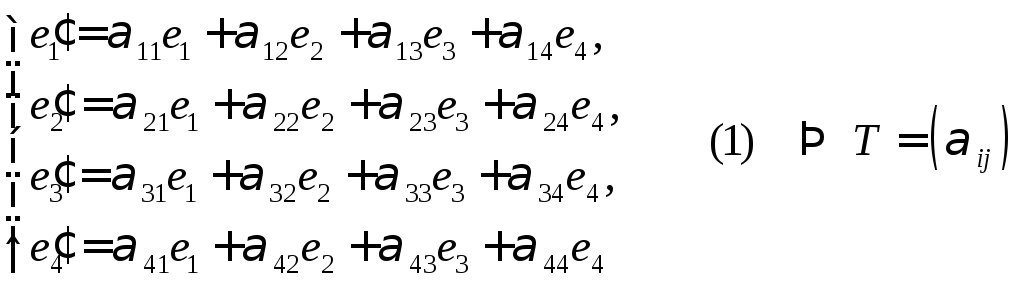
Підставимо дані многочлени в (1):

(2)

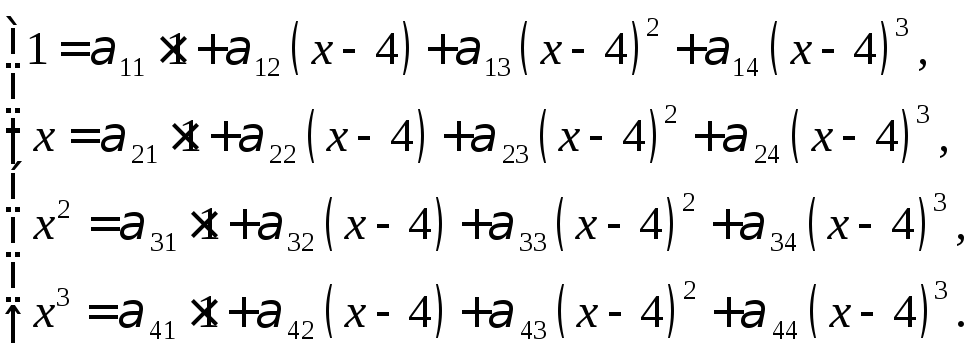
Оскільки в правій частині кожної рівності із (2) маємо розклад многочлена, що стоїть зліва, за степенями (у ряд Тейлора), то отримуємо:

Позначимо , тоді

Позначимо Тоді

Позначимо Тоді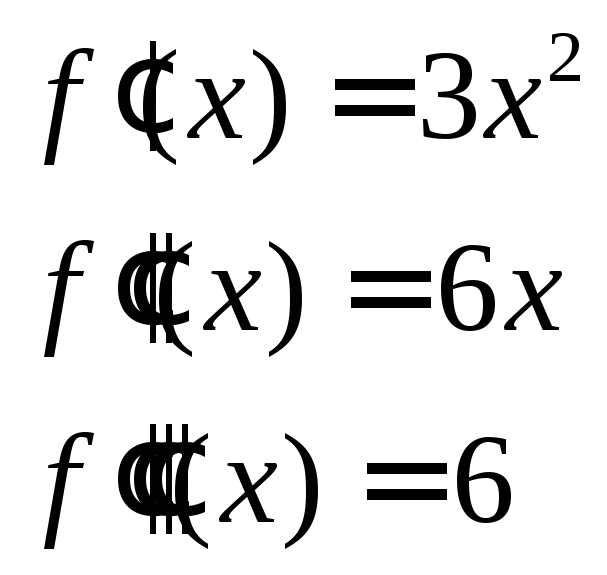

Отже, — матриця переходу від базидо базию