
- •Лінійний простір. Аксіоматика. Ізоморфізм.
- •Скінченновимірні лінійні простори. Базис. Розмірність простору. Перетворення базису.
- •Підпростори лінійного простору. Їх сума та перетин.
- •Перетин (переріз) лінійних підпросторів.
- •Сума підпросторів лінійного простору.
- •Теорема про зв’язок між розмінностями суми і перерізу лінійних підпросторів.
- •Лінійні оператори. Їх властивості
- •Область значень та ядро лінійного оператора.
- •Власні значення і власні вектори лінійного оператора.
Лінійний простір. Аксіоматика. Ізоморфізм.
Слід зазначити, що поняття лінійного простору є основним поняттям в лінійній алгебрі і одним з основних в математиці.
Перш
ніж перейти до поняття лінійного
простору, нагадаємо, що в І семестрі ми
вже зустрічалися з поняттям п-вимірного
векторного простору. п-вимірним
вектором називається набір
 .
.
Над ними можна виконувати дії:
додавання векторів:
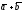 ;
;множення вектора на скаляр:
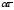
Виконуються властивості:

Але нам в різних розділах математики доводилося зустрічатися з різними об’єктами, для яких також вводилися аналогічні алгебраїчні операторії, які володіють всіма згаданими властивостями.
Наприклад:
– в алгебрі:
матриці одного порядку;
многочлени (від однієї чи багатьох змінних).
– в аналітичній геометрії:
вектори на площині чи в просторі;
– в математичному аналізі:
функції (від 1 чи багатьох змінних).
Пізніше ми будемо наводити інші приклади множин, у яких визначені операції множин, у яких визначені операції володіють вказаними властивостями.
Тому природно виникає необхідність дослідити множину, яка складається з елементів довільної природи, в якій визначено операції додавання елементів та множення елемента на число, котрі володіють цими властивостями.
Причому ці операції можуть бути визначені будь-яким способом, лише б вони задовольняли вказані властивості.
П.1. поняття лінійного простору. Аксіоми.
Розглянемо
довільну не порожню множину
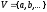
і
числове поле Р
(або множину
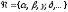 )
)
Нехай у множині V задано алгебраїчні операції:
додавання елементів множини V:
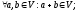
множення елемента із V на число з
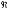 :
: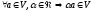
будемо вимагати, щоб введені операції задовольняли умови:
1)

2)
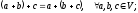
3)

4)

5)
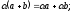
6)
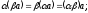
7)
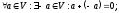
8)
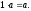
Означення 1: Множину V елементів довільної природи, в якій задано операції множення елементів множини V і множення елементів з V на дійсне число, котрі задовольняють умови 1)-8), називають дійсним лінійним (або дійсним вектором) простором.
Вимоги 1)-8) називають аксіомами лінійного простору.
Елементи множини V, незалежно від їх природи, називають векторами.
Якщо елементи множини V множаться на комплексні числа, то лінійний простір називаєть комплексним (або лінійним простором над полем комплексних чисел).
В курсі лінійної алгебри ми будемо вивчати дійсні лінійні простору, а з комплексними лінійними просторами Ви зустрінетеся в курсі «Комплексний аналіз» на ІІІ курсі.
Розглянемо важливі наслідки, які випливають з означення лінійного простору.
Наслідок 1: Нульовий елемент у V єдиний.
Дов. Проведемо від супротивного.
Припустимо, що є 2 нульові елементи:
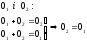
Наслідок
2: Протилежний
елемент
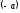 до елемента (а) єдиний.
до елемента (а) єдиний.
Дов.
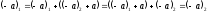
ІІ
спосіб. Припустимо, що 2 різні елементи
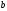 ,
с
– протилежні до а:
,
с
– протилежні до а:
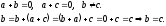
Наслідок
3: Рівняння
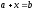 у лінійному просторіV
при довільних а і
у лінійному просторіV
при довільних а і
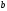 має
єдиний розв’язок:
має
єдиний розв’язок:
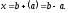 самостійно.
самостійно.
Наслідок
4:
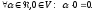
Дов.
Розглянемо

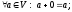
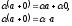
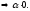
Наслідок
5:

Наслідок
6: Якщо
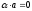 ,
то
,
то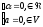
Наслідок
7:
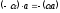
Наслідок
8:

Наслідок
9:
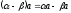
Наслідок
10:
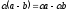
Приклади лінійних просторів.
1. Сукупність всіх многочленів від х, степінь яких не перевищує п, із звичайними операціями додавання сногочленів і множення многочленна на дійсне число.
2.
Множина многочленів степеня рівно п
лінійного простору не утворює (відносно
«+» і « »
на дійсне число).
»
на дійсне число).
3. Множина всіх матриць п-го порядку з дійсними елементами відносно додавання матриць і множення матриці на дійсне число.
4. Множина комплексних чисел відносно додавання чисел і множення компл. числа на дійсне число.
5.
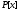 – множина всіх многочленів відх
з дійсними коефіцієнтами довільного
степеня.
– множина всіх многочленів відх
з дійсними коефіцієнтами довільного
степеня.
Ізоморфізм лінійних просторів.
Нехай
задано два лінійні простори
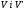 .
.
Припустимо, що задано взаємно однозначне відображення (бієкція) f:
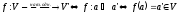 ,
яке кожному вектору
,
яке кожному вектору
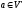 ставить у відповідність єдиний вектор
ставить у відповідність єдиний вектор .
.
Взаємна однозначність означає наступне:
Якщо
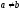 вV,
то
вV,
то
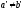 у
у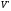 .
.
Означення
2: Відображення
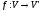 називаютьізоморфним
відображенням (або
ізоморфізмом)
простору
називаютьізоморфним
відображенням (або
ізоморфізмом)
простору
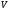 та
та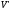 ,
якщо воно задовольняє вимоги:
,
якщо воно задовольняє вимоги:
1)
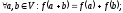
2)
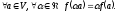
Означення
3: Якщо
існує ізоморфізм простору
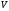 на
простір
на
простір ,
то такі лінійні простори називаютьізоморфними.
Це позначається:
,
то такі лінійні простори називаютьізоморфними.
Це позначається:
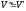
Якщо навмання два лінійні простори, то вони не обов’язково будуть ізоморфними.
Оскільки
ізоморфне відображення
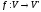 лінійних просторів
лінійних просторів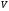 та
та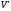 є взаємно однозначним, то для нього
існує обернене відображення
є взаємно однозначним, то для нього
існує обернене відображення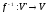 ,
яке також є ізоморфним.
,
яке також є ізоморфним.
З абстрактної точки зору ізоморфні лінійні простори нічим не відрізняються. Проте, їх елементи можуть мати різну природу.
Властивості ізоморфізму.
1)
Якщо лінійні простори
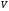 та
та
 ізоморфні,
тол образом нуля
ізоморфні,
тол образом нуля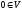 є нуль
є нуль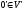 .
.
Дійсно,
 –ізоморфізм.
–ізоморфізм.
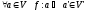
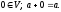 Нехай
Нехай
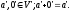
Розглянемо:
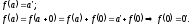
2)
Якщо
лінійні простори
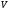 та
та
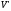 ізоморфні,
то образом вектора
ізоморфні,
то образом вектора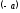 ,
протилежного до вектора
,
протилежного до вектора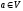 є вектор, протилежний до його образа,
тобто
є вектор, протилежний до його образа,
тобто
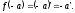
(доведення аналогічно до 1)
Оскільки елементи дійсного лінійного простору можна назвати векторами, то для них можемо застосувати поняття лінійної залежності так, як це робилося для п-вимірних векторів.
Нагадаємо:
система векторів
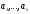 називається лінійно залежною, якщо
називається лінійно залежною, якщо такі числа
такі числа ,
хоч одне з яких
,
хоч одне з яких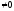 ,
що
,
що
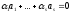 .
.
Ізоморфне відображення лінійних просторів лінійно залежну систему векторів із V відображає в лінійно залежну систему із
 .
.
Нехай
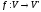 – ізоморфне відображення.
– ізоморфне відображення.
І
нехай система векторів
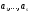 – лінійно залежна уV:
– лінійно залежна уV:
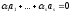 ,
де не всі
,
де не всі
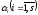 рівні нулю.
рівні нулю.
Знайдемо образ обох частин при відображенні f:
л.ч.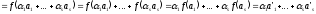
п.ч.

причому
не всі

тобто
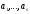 – лінійно залежна система.
– лінійно залежна система.
Аналогічно можна переконатися, що при ізоморфному відображенні лінійно незалежна система векторів відображаються в лінійно незалежну систему.
