- •Лінійний простір. Аксіоматика. Ізоморфізм.
- •Скінченновимірні лінійні простори. Базис. Розмірність простору. Перетворення базису.
- •Підпростори лінійного простору. Їх сума та перетин.
- •Перетин (переріз) лінійних підпросторів.
- •Сума підпросторів лінійного простору.
- •Теорема про зв’язок між розмінностями суми і перерізу лінійних підпросторів.
- •Лінійні оператори. Їх властивості
- •Область значень та ядро лінійного оператора.
- •Власні значення і власні вектори лінійного оператора.
Скінченновимірні лінійні простори. Базис. Розмірність простору. Перетворення базису.
Означення скінченновимірного лінійного простору.
Означення
1: Лінійно
незалежну систему векторів лінійного
простору V
будемо називати максимальною
лінійно незалежною,
якщо після приєднання
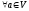 вона перетвоюється в лінійно залежну.
вона перетвоюється в лінійно залежну.
Слід зауважити, що не в кожному лінійному просторі є максимальна лінійно незалежна система векторів.
Прикладом простору, у якому немає максимально лінійно незалежної системи векторів є простір всіх многочленів з коефіцієнтами з поля Р.
(бо
якщо припустити, що
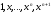 –
теж лінійно залежна система многочленів)
–
теж лінійно залежна система многочленів)
Означення 2: Лінійний простір називається скінченновимірним, якщо він має хоча б одну максимальну лінійну незалежну систему векторів.
Якщо такої системи не існує, то він називається нескінченновимірним.
Ми будемо вивчати тільки скінченновимірні простори.
Нескінченновимірні простори будете вивчати в курсі функціонального аналізу.
Доведемо наступну теорему.
Теорема: Якщо в лінійному просторі V існує максимальна лінійно незалежна система з п ізоморфний п-вимірному просторі векторів –рядків.
Дов. Нехай V – лінійний простір, в якому є максимальна лінійно незалежна система векторів, які складаються з п векторів:
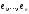 .
.
Розглянемо
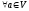 .
Система векторів
.
Система векторів
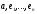 –лінійно
залежна
–лінійно
залежна
 числа
числа такі, що
такі, що ,
причому хоч один з коефіцієнтів
,
причому хоч один з коефіцієнтів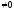 .
.
Якщо
хоч один
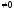 ,
то є безліч наборів такого типу. Тоді
можна вибрати
,
то є безліч наборів такого типу. Тоді
можна вибрати .
.
Наприклад
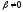 .
Тоді
.
Тоді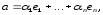 де
де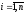 (1)
(1)
Таким чином, розглянемо відповідність:
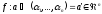 (2)
(2)
З’ясуємо,
чи буде ця відповідність взаємно
однозначним. Припустимо, що існує ще
один (інший) образ елемента
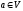 при відповідностіf:
при відповідностіf:
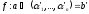
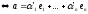 (3)
– так ми визначили відображення f.
(3)
– так ми визначили відображення f.
Віднімемо (1) – (3):
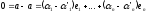
Згідно
з умовою, система елементів
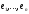 –лінійно незалежна. Тому всі коефіцієнти
= 0.
–лінійно незалежна. Тому всі коефіцієнти
= 0.

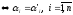
Це означає, що так вибране відображення (2) є взаємно однозначним.
Покажемо,
що f
– ізоморфізм. Для цього розглянемо
довільний елемент
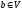 тоді:
тоді:
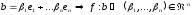
Перевіримо аксіоми ізоморфізму:
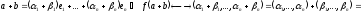
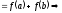 1)
виконується.
1)
виконується.
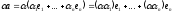
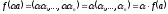
 2)
– виконується.
2)
– виконується.
Це доводить, що відображення f є ізоморфним.
Отже, даний простір V ізоморфний п-вимірному векторному простору векторів –рядків.
На основі властивості з ізоморфізму можна зробити висновок:
При
ізоморфній відповідності лінійних
просторів максимальна лінійно незалежна
система векторів простору V
відображається в максимальну лінійно
незалежну систему векторів простору
 і
навпаки.
і
навпаки.
Нам з І семестру відомо, що всі максимально лінійно незалежного простору векторів т-вимірного простору векторів –рядків мають по п векторів, тому і всі максимальні системи елементів задано простору V мають по п векторів.
Базис і розмірність скінченновимірного простору.
Означення 3: Будь-яку максимальну лінійно незалежну систему елементів скінченновимірного векторного простору називають базою (базисом) цього простору.
Домовимося базу п-вимірного простору V позначати:

Якщо в одному і тому ж просторі розглянути декілька баз , то всі вони мають однакову кількість векторів.
Доведення
цього аналогічне доведення такого є
факту для п-вимірного
простору
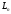 .
.
Означення
4: Кількість
векторів, що входять в будь-яку базу
скінченновимірного лінійного простору
V
називають розмірністю
або
цього простору і позначають

Повернемося до попередніх прикладів (попередня тема П.2.)
1)
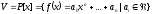 ,
база:
,
база: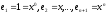 ,
,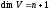
3)
 ,
база:
,
база:
4)
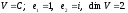
5) нескінченновимірний – бо максимально лінійно незалежної системи векторів немає.
Правильними є наступні твердження:
Твердження 1: У просторі V, що має розмірність п, кожна лінійно незалежна система з п елементів утворює базис.
Твердження 2: У п-вимірному просторі кожна лінійно незалежна система п векторів є базисом цього простору.
Твердження
3: Будь-який
лінійний простір V
розмірності п ізоморфний простору
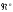
Твердження 4: Всі лінійні простори, які мають однакову розмірність, ізоморфні між собою.
І
навпаки, якщо простори
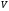 та
та
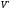 такі,
що
такі,
що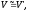 то
то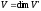 .
.
Оскільки,
всі простори розмірності п
ізоморфні до
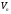 ,
то вони ізоморфні між собою. Має місце
і навпаки.
,
то вони ізоморфні між собою. Має місце
і навпаки.
Координати вектора в заданому базисі.
Нехай
V
–
простір розмірності п.
Будемо його позначати
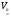 (щоб зафіксувати розмірність).
(щоб зафіксувати розмірність).
Розглянемо
приклад бази у
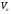 :
:
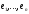
Нехай
 – довільний елемент цього простору. Як
уже зазначали, вектора
можна розкласти за векторами цієї бази:
– довільний елемент цього простору. Як
уже зазначали, вектора
можна розкласти за векторами цієї бази:
 ,
причому числа
,
причому числа
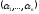 визначник однозначно для даного базису
визначник однозначно для даного базису
Означення
5: Координати
елемента
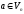 відносно базису
відносно базису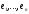 називається
коефіцієнти розкладу цього елемента
по даному базису.
називається
коефіцієнти розкладу цього елемента
по даному базису.
Позначається:
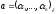
Приклад:
1)
У
дійсному лінійному просторі векторів
 координати вектора
координати вектора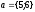 у базі
у базі
а)
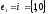
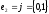 такі:
такі:
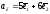
б)
у базі

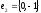 такі:
такі:
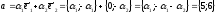
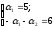

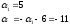
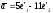
2)
розкладемо многочлен
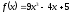 із простору многочленів степеня
із простору многочленів степеня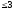 по базису
по базису
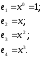

Зв’язок між базисами.
У прикладі 1) бачимо, що координати одного і того ж вектора відрізняються залежно від того, який базис було вибрано.
Розглянемо
дійсний простір
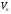 розмірностіп.
розмірностіп.
Розглянемо два різні базиси цього простору:
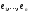 –базис
–базис
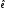 (1)
(1)
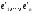 –базис
–базис
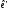 (2)
(2)
Оскільки
елемент
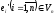 ,
то їх можна розкласти за елементами
базису
,
то їх можна розкласти за елементами
базису
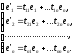 (3)
(3)
 ,
,
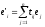
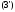
З коефіцієнтів розкладу складемо матрицю
 (4)
(4)
Матрицю
Т
називають матрицею
переходу від бази
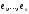 до
до
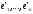
3) можна записати скорочено, враховуючи позначення:
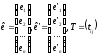
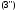
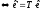 ,
де Т
– перехід від
,
де Т
– перехід від
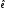 до
до
Очевидно, порядок матриці Т завжди буде збільшуватися з розмірністю простору V.
Матриця переходу Т невироджена.
В
протилежному випадку рядки матриці Т
були б лінійно залежними, а це не означало
би, що вектори
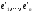 лінійно залежними, що суперечить умові,
що вони утворюють базу.
лінійно залежними, що суперечить умові,
що вони утворюють базу.
Формули
(3),
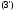 ,
,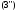 називаютьформулами
зв’язку між базами або
формулами
перетворення баз (1) і (2).
називаютьформулами
зв’язку між базами або
формулами
перетворення баз (1) і (2).
Аналогічно
вектори бази
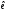 можна
виразити через вектори
можна
виразити через вектори :
:
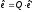 (5)
(5)
Тут
Q
–матриця переходу від бази
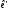 до бази
до бази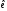 .
У її рядках стоять коефіцієнти розкладу
векторів бази
.
У її рядках стоять коефіцієнти розкладу
векторів бази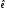 по векторах бази
по векторах бази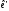 .
.
Приклад:
у дійсному лінійному просторі многочленів
від х
степеня
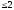 з дійсними коефіцієнтами. Знайти матрицю
переходу від бази
з дійсними коефіцієнтами. Знайти матрицю
переходу від бази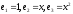 до бази
до бази
Розв’язання:
потрібно
знайти коефіцієнти розкладу векторів
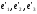 через вектори
через вектори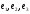 :
:
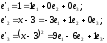
Отже,
 – матриця переходу від
– матриця переходу від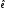 до
до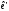 .
.
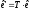 .
.
З’ясуємо, чи існує зв’язок між матрицями Т і Q.
Для
цього в 5) замість
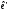 підставити вираз із
підставити вираз із :
:
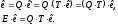
Аналогічно:

Висновок:
Матриці
переходу від бази
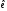 до
до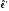 є
взаємно оберненими.
є
взаємно оберненими.
П.5. Зв’язок між координатами вектора в різних базисах.
Нехай
лінійному просторі
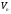 задано дві бази:
задано дві бази:
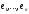 –базис
–базис
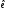 (1)
(1)
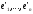 –базис
–базис
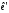 (2)
(2)
Між якими існує зв’язок
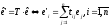 (3)
(3)
де
Т
– матриця переходу від
 до
до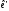 .
.
Розглянемо
довільний вектор
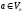 його можна розкласти за цими базами:
його можна розкласти за цими базами:
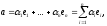 (4)
(4)
 (5)
(5)
Тоді
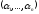 – координати вектораа
в
базисі
– координати вектораа
в
базисі
 (старий базис),
(старий базис), – координати вектораа
в базисі
– координати вектораа
в базисі
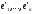 (новий базис).
(новий базис).
Знайдемо зв’язок між цими координатами, враховуючи зв’язок між базами:

Отже, можна записати:
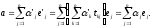
Оскільки
вектори
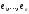 – лінійно незалежні, то така рівність
векторів рівносильна рівності відповідних
координат:
– лінійно незалежні, то така рівність
векторів рівносильна рівності відповідних
координат:
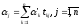 (6)
(6)
Остання
рівність записується в матричному
вигляді:

або, скорочено:
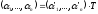 (7)
(7)
чи
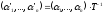 (8)
(8)
де
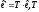 –
переходить від
–
переходить від
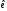 до
до
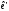
формули (7) і (8) задають закони перетворення координат одного і того ж вектора в різниз базах.
Приклад:
Вектор
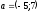 і
і
вектори
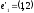 і
і задано в базі
задано в базі .
.
Розв’язання:
у
базі
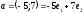
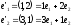
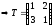
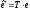
Скористаємось формулами (8):
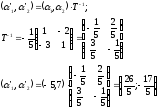
Отже,