
- •Приклади розв’язування задач Лінійні простори
- •1. Довести, що множина всіх многочленів степеня не вище 3 з дійсними коефіцієнтами, для яких , утворює дійсний лінійний простір. Вказати приклад бази та розмірність цього простору.
- •3. Довести, що множина матриць третього порядку, симетричних відносно обох діагоналей з дійсними елементами, утворює дійсний лінійний простір. Знайти довільний базис і розмірність цього простору.
- •4. У дійсному лінійному просторі многочленів степеня не вище 3 знайти матрицю переходу від базису до базису
- •5. У дійсному лінійному просторі знайти матрицю переходу від бази до а).
- •6. Переконатись, що многочлени утворюють базис у лінійному просторі многочленів степеня не вище 4. Знайти координати многочленау цьому базисі.
- •7. Довести, що кожна з систем векторів
- •8. Знайти розмірності суми і перетину лінійних підпросторів натягнутих на систему векторів:
- •17. З’ясувати, які з наступних матриць можна звести до діагонального виду шляхом переходу до нового базису:
5. У дійсному лінійному просторі знайти матрицю переходу від бази до а).
Розв’язок
Позначимо
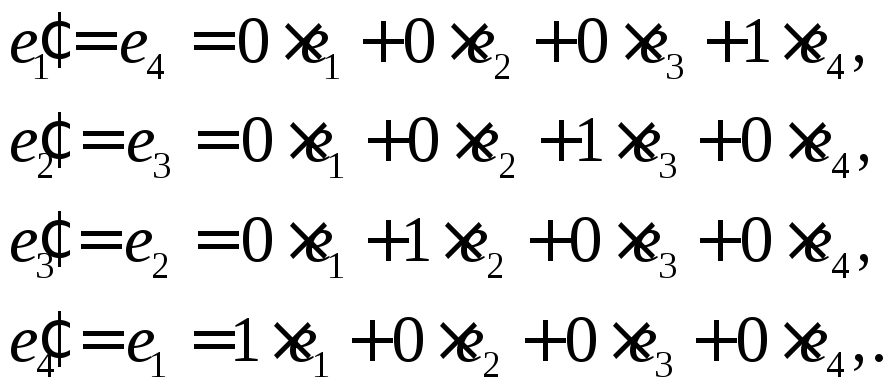
Звідси
 — матриця переходу від базису
— матриця переходу від базису
![]() до базису
до базису
![]() .
.
б)
![]()
Розв’язок
Позначимо
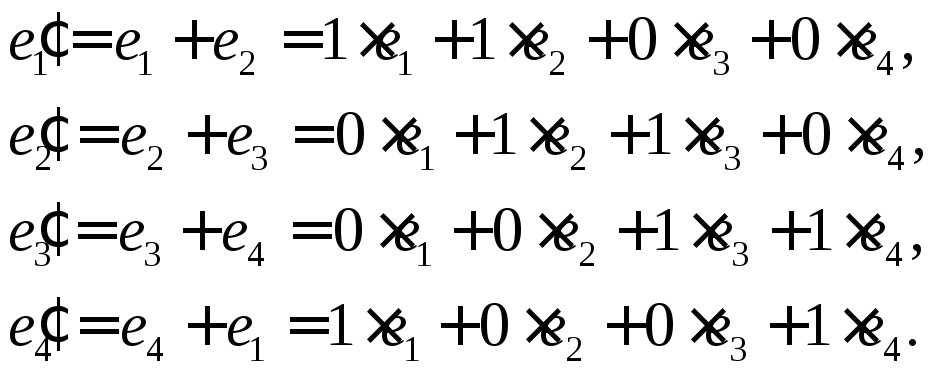
Звідси
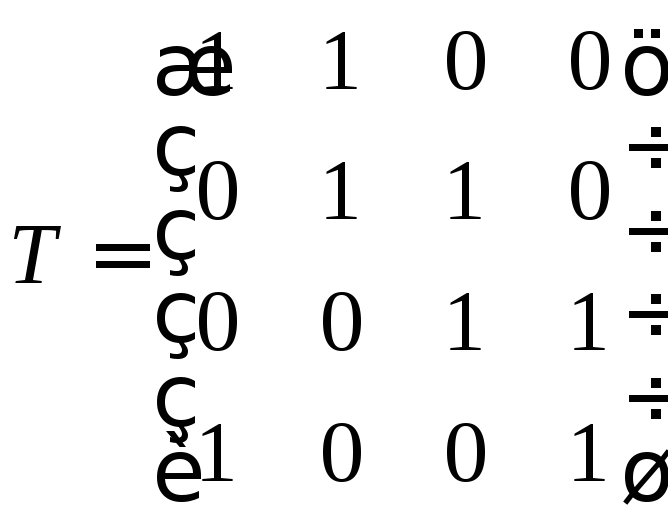 —шукана матриця переходу
від базису
—шукана матриця переходу
від базису
![]() до базису
до базису
![]()
6. Переконатись, що многочлени утворюють базис у лінійному просторі многочленів степеня не вище 4. Знайти координати многочленау цьому базисі.
Розв’язок
Позначимо:
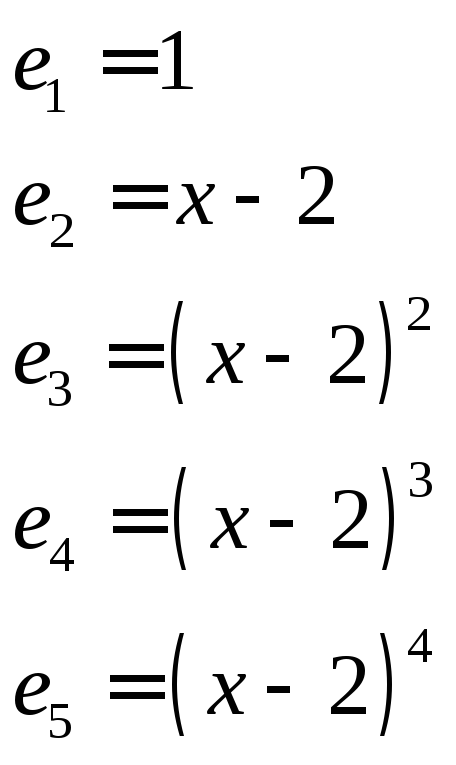
Елементи
![]() утворюють базис тоді, і тільки тоді,
коли: а) вони лінійно незалежні; б)
дописування до них
утворюють базис тоді, і тільки тоді,
коли: а) вони лінійно незалежні; б)
дописування до них![]() елемента цього ж простору перетворює
систему на лінійно залежну.
елемента цього ж простору перетворює
систему на лінійно залежну.
Перевіримо тому умови а) і б):
а)
![]()
(1)
![]() — лінійно незалежні.
— лінійно незалежні.
Отже дослідимо, якими можуть
бути коефіцієнти
![]() у рівності (1):
у рівності (1):
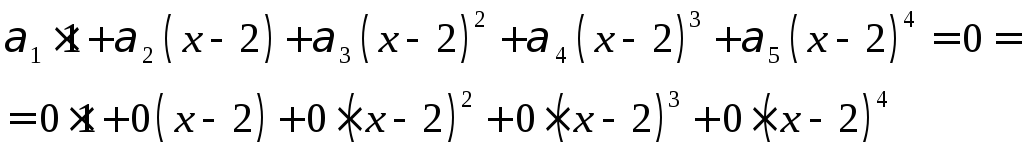
(Скористаємося тим, що кожен
многочлен, в тому числі й нульовий можна
єдиним способом розкласти за степенями
![]() ).
).
Отже,
![]() — лінійно незалежна система.
— лінійно незалежна система.
б)
![]() —чи максимальна?
—чи максимальна?
Оскільки розмірність простору
многочленів степеня
![]() рівна 5, то довільна система з 6 та більше
многочленів завжди є лінійно залежною,
а тому для довільного многочлена
рівна 5, то довільна система з 6 та більше
многочленів завжди є лінійно залежною,
а тому для довільного многочлена![]() степеня не вище 4 маємо, що
степеня не вище 4 маємо, що![]() ,
,![]() — лінійно залежні
— лінійно залежні![]()
![]() — базис простору многочленів степеня
не вище 4.
— базис простору многочленів степеня
не вище 4.
Для того, щоб знайти координати
многочлена
![]() у заданому базисі, розкладемо його в
ряд Тейлора за степенями
у заданому базисі, розкладемо його в
ряд Тейлора за степенями![]() :
:
-
-2
0
12
-3
2
2
-2
-4
4
5
12
2
-2
-8
-12
-19
2
-2
-12
-36
2
-2
-16
2
-2
Отже,
![]()
![]() —координати
—координати
![]() в базисі
в базисі![]() .
.
7. Довести, що кожна з систем векторів
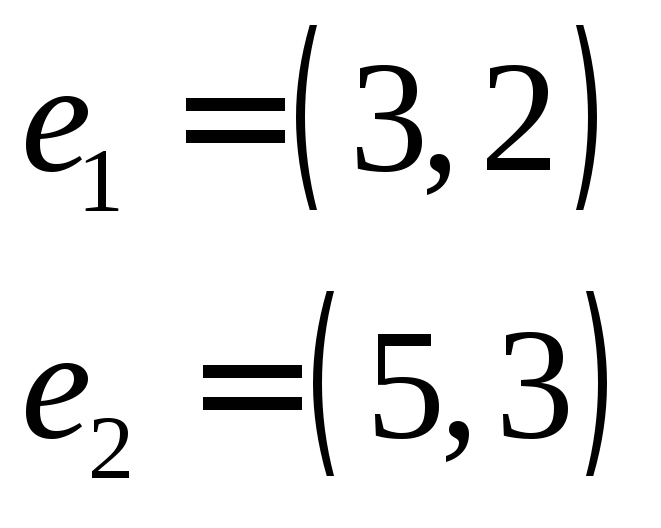 та
та
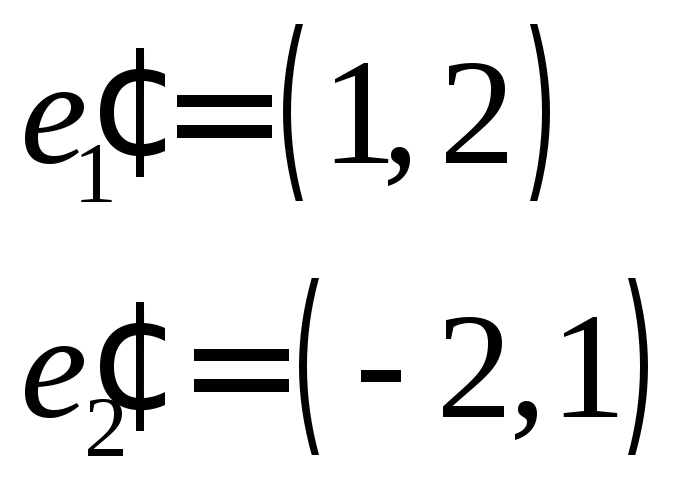 є базисом лінійного простору
є базисом лінійного простору![]() .
Знайти зв’язок між координатами одного
і того ж вектора відносно цих базисів.
.
Знайти зв’язок між координатами одного
і того ж вектора відносно цих базисів.
Розв’язок
Оскільки
![]() і в кожній системі векторів є по 2 вектори,
то вони будуть базисами тоді, і тільки
тоді, коли є лінійно незалежними.
і в кожній системі векторів є по 2 вектори,
то вони будуть базисами тоді, і тільки
тоді, коли є лінійно незалежними.
Вектори, задані своїми
координатами, лінійно незалежні тоді,
і тільки тоді, коли ранг системи векторів
= кількості цих векторів. Отже,
![]()
та
![]() —
базис у
—
базис у![]()
![]() —теж базис у
—теж базис у
![]() .
.
Нехай
![]() — довільний вектор простору
— довільний вектор простору![]() .
.
Нехай
![]() — координати вектора
— координати вектора![]() в базисі
в базисі![]() .
Аналогічно,
.
Аналогічно,
![]() —координати вектора
—координати вектора
![]() в базисі
в базисі![]() .
Тоді
.
Тоді![]() ,
де
,
де![]()
![]() — матриця переходу від
— матриця переходу від![]() до
до![]() .
.
Позначимо
![]() — базис, у якому задано координати
векторів
— базис, у якому задано координати
векторів![]() та
та![]() .
Тоді
.
Тоді
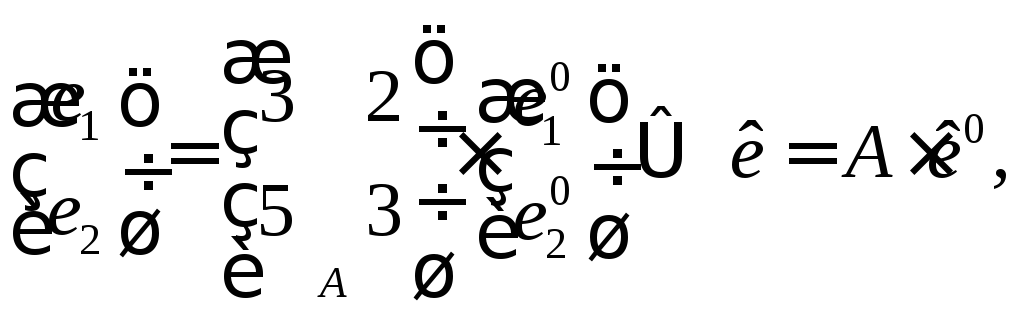 та
та
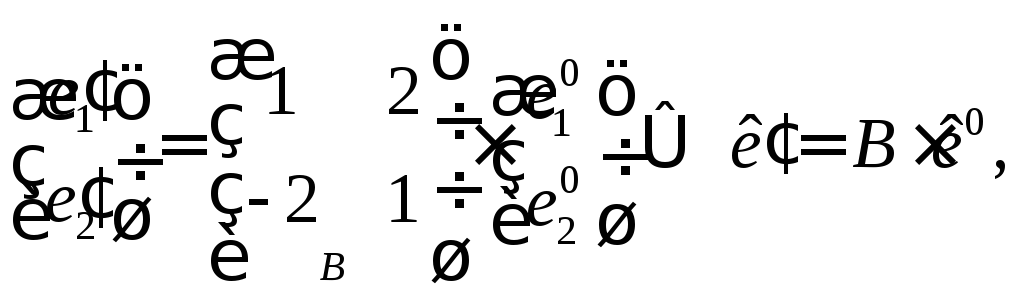
Звідси маємо:
![]()
Отже,
![]() та
та![]()
![]() .
.
 .
.
Звідси маємо:
 — зв’язок між координатами одного
вектора в різних базах.
— зв’язок між координатами одного
вектора в різних базах.
8. Знайти розмірності суми і перетину лінійних підпросторів натягнутих на систему векторів:
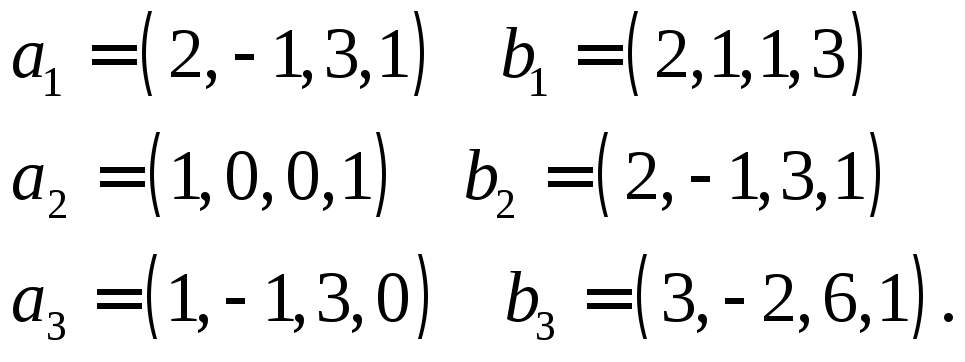
Розв’язок
Нехай
![]()
![]()
Тоді
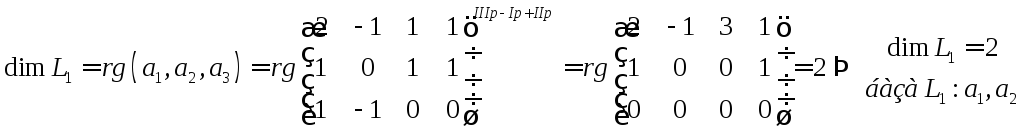 .
.
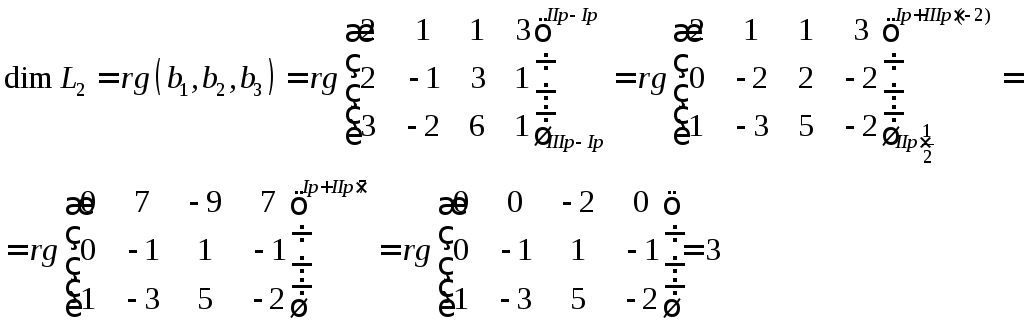
Отже
![]() база
база![]()

Отже, враховуючи формулу
![]() .
База
.
База
![]() :
:![]() .
.
Враховуючи формулу
![]() маємо, що
маємо, що
![]()
Відповідь:
Лінійні оператори
9. У дійсному лінійному
просторі многочленів
![]() степеня
не вище 4 задано оператор
степеня
не вище 4 задано оператор![]() Довести, що цей оператор лінійний і
знайти його матрицю в базі
Довести, що цей оператор лінійний і
знайти його матрицю в базі![]()
Розв’язок
Оператор
![]() буде лінійними тоді, і тільки тоді, коли
буде лінійними тоді, і тільки тоді, коли
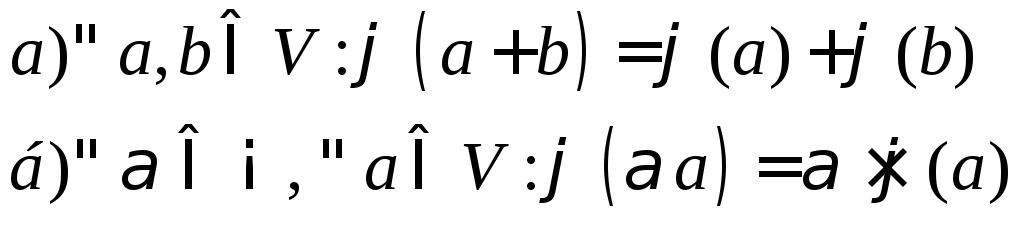
Перевіримо ці умови для
заданого оператора
![]() ,
де
,
де![]()
а) Нехай
![]() .Тоді
.Тоді

б)
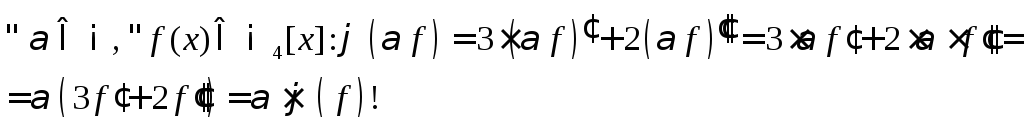
Отже, умови а) та б) виконуються
![]()
![]() — лінійний оператор.
— лінійний оператор.
Матриця лінійного оператора
![]() в базі
в базі![]() складається з коефіцієнтів розкладу
образів базисних векторів по заданому
базису. Тому маємо:
складається з коефіцієнтів розкладу
образів базисних векторів по заданому
базису. Тому маємо:
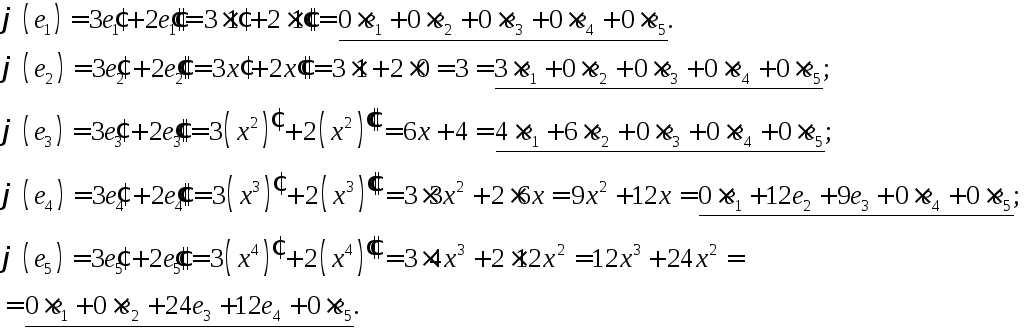
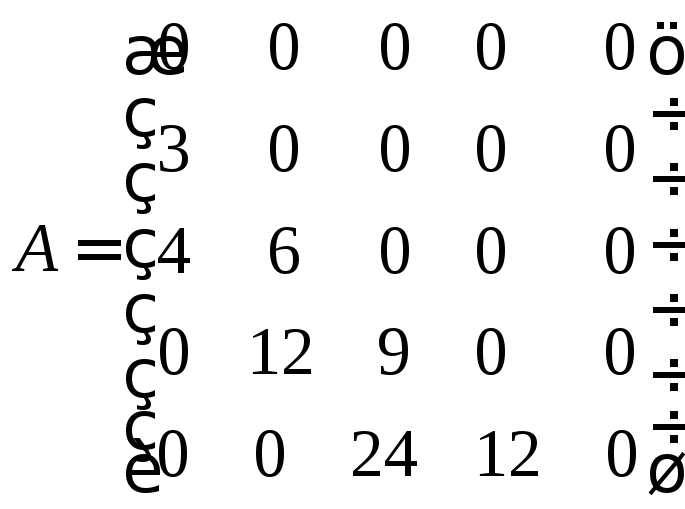
Із коефіцієнтів підкреслених
рівностей виписуємо шукану матрицю
оператора
![]() :
:
10. Довести, що є лінійним
оператор
![]() простору векторів з дійсними координатами
простору векторів з дійсними координатами![]() (у якому визначене звичайне скалярне
множення векторів), котрий діє з правилом
(у якому визначене звичайне скалярне
множення векторів), котрий діє з правилом![]() де
де![]() .
Знайти матрицю цього оператора в базисі
.
Знайти матрицю цього оператора в базисі![]() .
.
Розв’язок
а)
![]()
![]()
б)
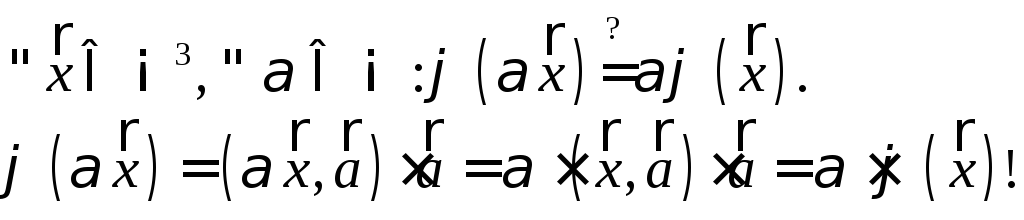
Отже,
![]() — лінійний оператор.
— лінійний оператор.
Знайдемо матрицю цього
оператора в базисі
![]()
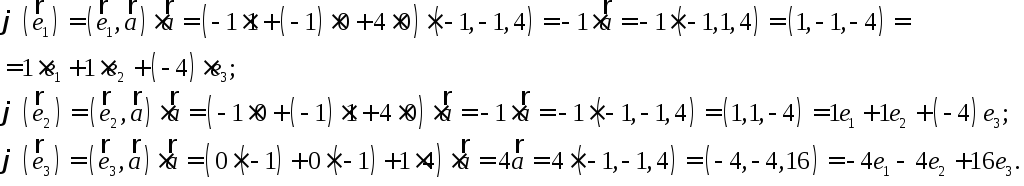 Отже,
Отже,
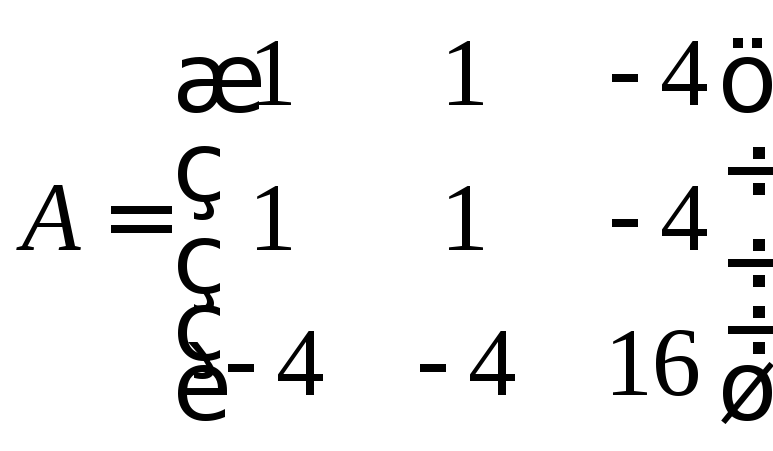 — матриця лінійного оператора
— матриця лінійного оператора![]() в базі
в базі![]() .
.
11. Задано лінійний простір
![]() і оператор
і оператор![]() .
Довести, що
.
Довести, що![]() — лінійний оператор і знайти його
матрицю в базі
— лінійний оператор і знайти його
матрицю в базі![]() .
.
Розв’язок
Перевіряємо умови лінійного оператора:
а)
![]()
![]()
![]()
![]()
![]()
![]() — виконується!
— виконується!
б)
![]()
![]()
![]() — виконується!
— виконується!
Умови а) і б) означення лінійного
оператора виконуються, отже
![]() — лінійний оператор.
— лінійний оператор.
Шукаємо матрицю оператора
![]() в базі
в базі![]() .
.
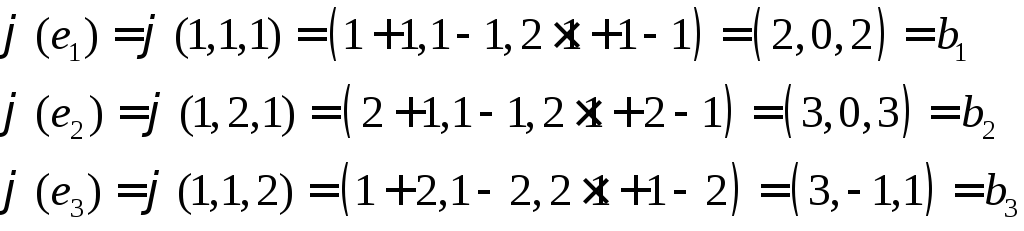
Знайдемо тепер коефіцієнти
розкладу кожного з векторів
![]() по базису
по базису![]() .
.
![]() ,
де
,
де
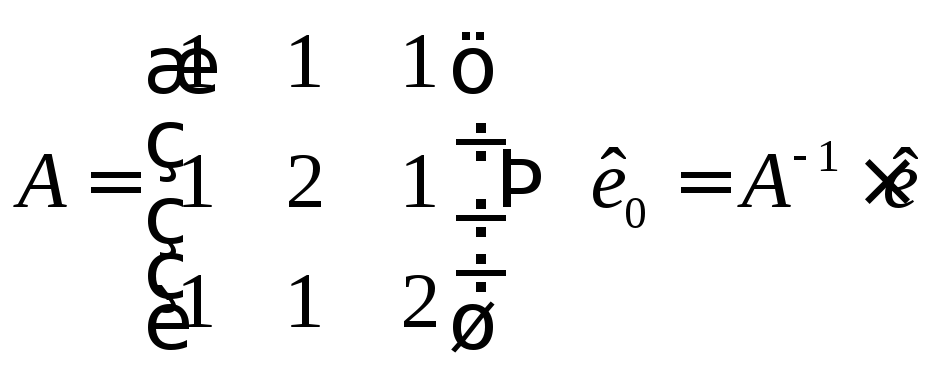
![]() ,
де
,
де

Тоді
![]() .
.
Отже,
![]() — матриця оператора
— матриця оператора![]() в базі
в базі![]() .
Знайдемо її елементи.
.
Знайдемо її елементи.
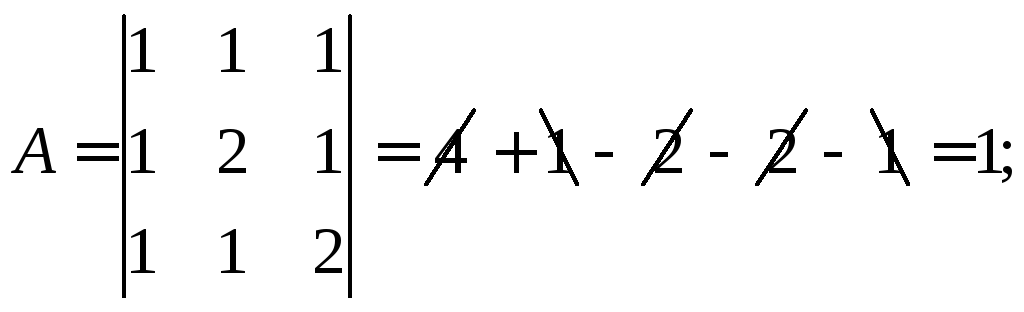
![]()
![]()
![]()
![]()
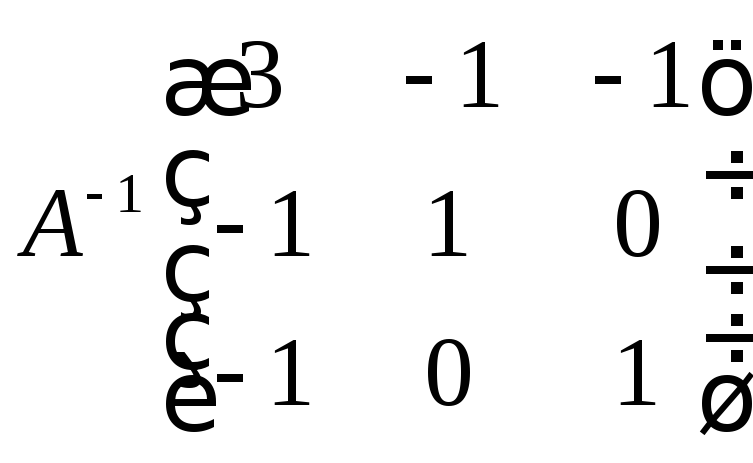
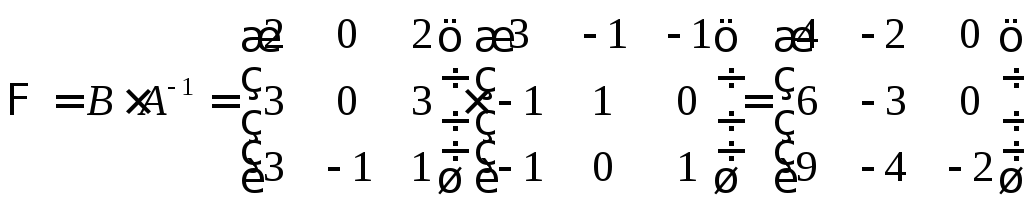 —шукана матриця лінійного
оператора
—шукана матриця лінійного
оператора
![]() в базисі
в базисі![]() .
.
12. Знайти матрицю оператора
![]() у просторі матриць другого порядку з
дійсними елементами у базисі
у просторі матриць другого порядку з
дійсними елементами у базисі![]()
Розв’язок

Отже,
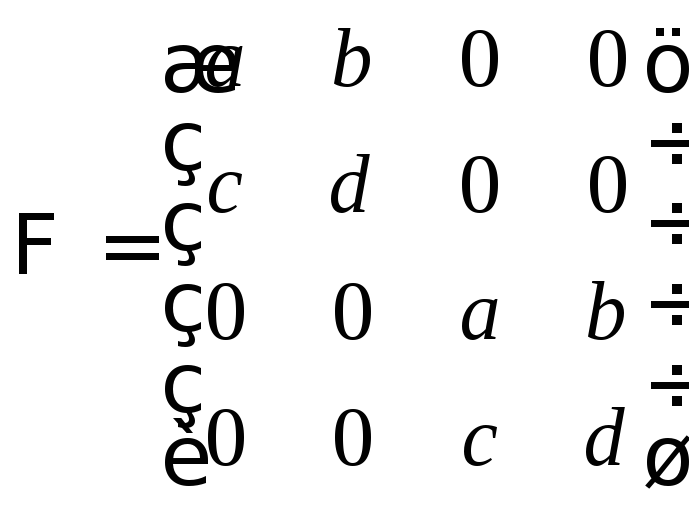 — матриця даного оператора
— матриця даного оператора![]() у базисі
у базисі![]() .
.
13. Лінійний оператор
![]() у базі
у базі![]() задано матрицею
задано матрицею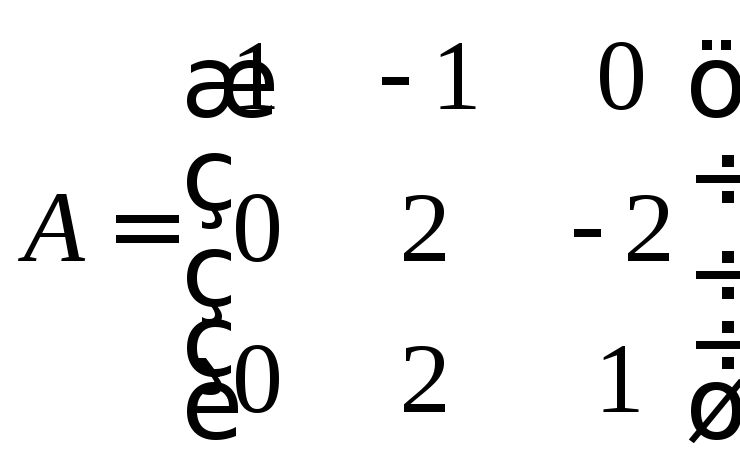 .
Знайти матрицю цього оператора в базисі
.
Знайти матрицю цього оператора в базисі![]()
Розв’язок
Якщо
![]() — шукана матриця оператора
— шукана матриця оператора![]() в базисі
в базисі![]() .
Тоді
.
Тоді![]() де
де![]() ,
,![]() — матриця переходу від бази
— матриця переходу від бази![]() до бази
до бази![]() .
Знайдемо її.
.
Знайдемо її.
![]() ,
де
,
де

![]()
![]() ,
де
,
де
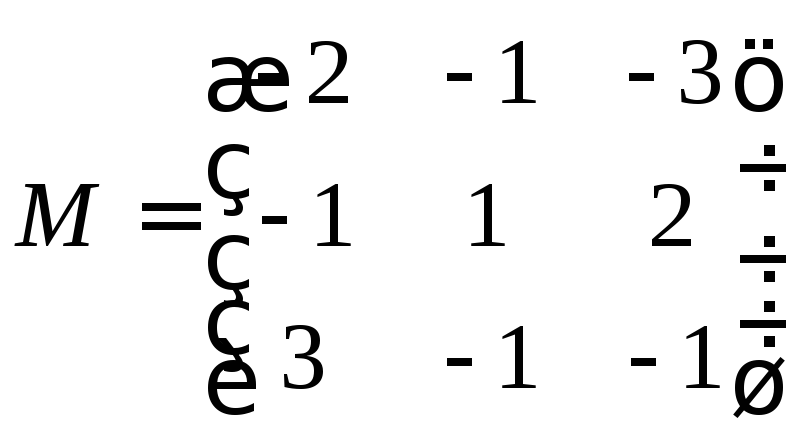 .
Тоді
.
Тоді![]()
Отже,
![]() .
.
Шукаємо
![]()
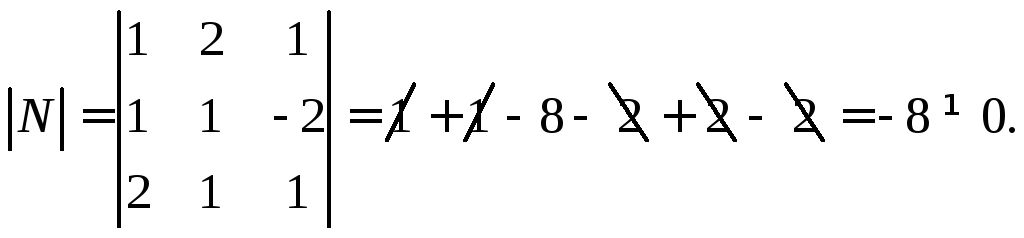

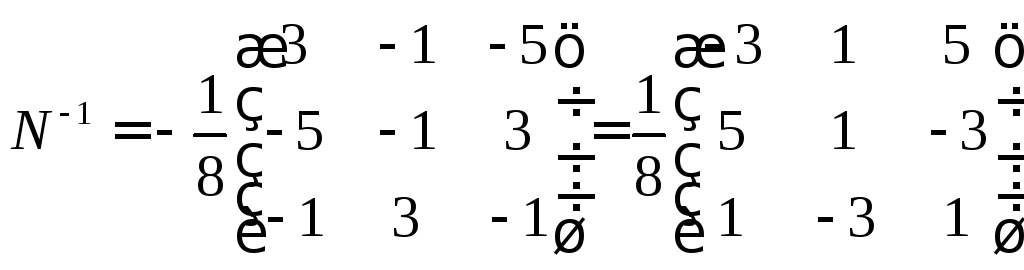
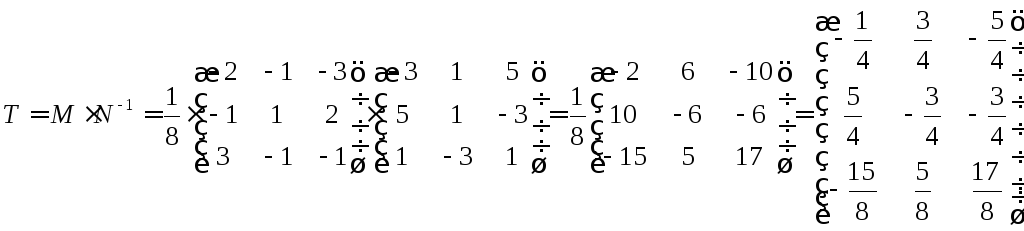
Шукаємо тепер
![]() :
:
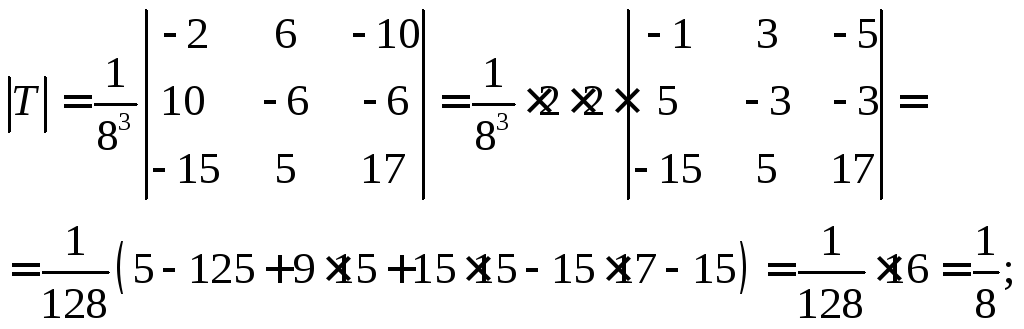

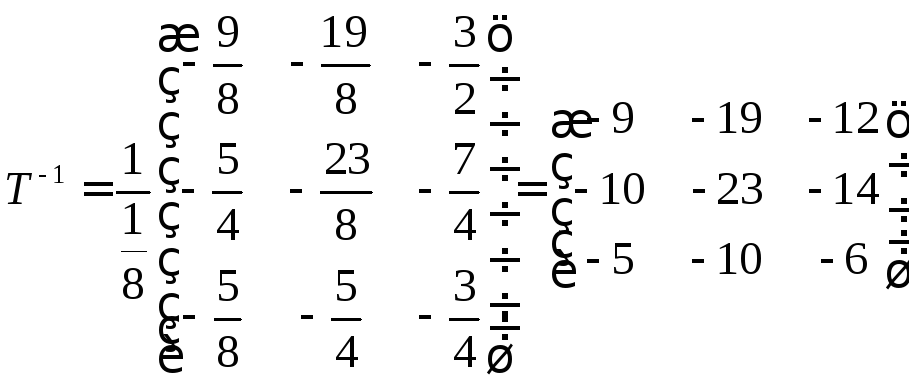

14. Знайти ядро та образ
лінійного оператора, заданого у деякому
базисі матрицею
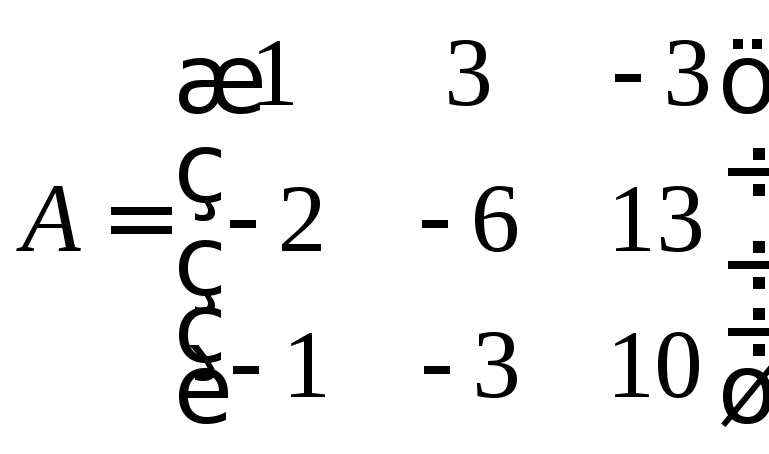 .
Чому дорівнює ранг та дефект цього
оператора?
.
Чому дорівнює ранг та дефект цього
оператора?
Розв’язок
Ядро оператора
![]() :
:
![]() (1)
(1)
Оскільки
![]() — матриця 3-го порядку, то
— матриця 3-го порядку, то![]() .
Нехай
.
Нехай![]() в тому ж базисі, що й задано матрицею
в тому ж базисі, що й задано матрицею![]() ,
має координати
,
має координати
![]()
Тоді із (1) маємо:
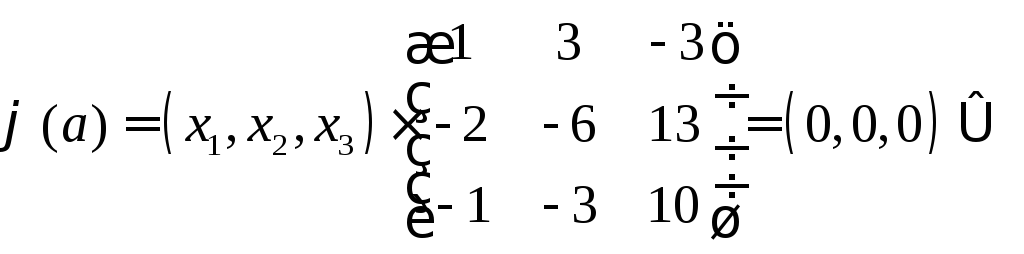
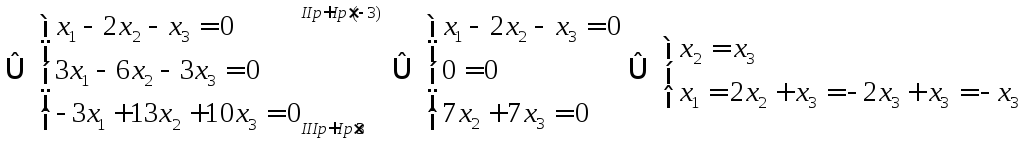
![]() —
—![]() —ядро.
—ядро.
![]() ,
бо база в
,
бо база в
![]() містить лише один елемент, наприклад
містить лише один елемент, наприклад![]() .
.
Отже, дефект оператора
![]() .
.
Образ оператора
![]() :
:
![]()

Отже,
![]() — ранг оператора
— ранг оператора![]() .
.
15. Знайти ядро і образ
лінійного оператора
![]()
Розв’язок
![]()
Нехай
![]()

Отже,
![]() — містить лише нульовий вектор
— містить лише нульовий вектор![]() Оскільки
Оскільки![]() то
то![]() — образом оператора
— образом оператора![]() є весь лінійний простір
є весь лінійний простір![]() ю
ю
16. Знайти власні значення та власні вектори лінійних операторів, що задаються в деякому базисі матрицею
а)
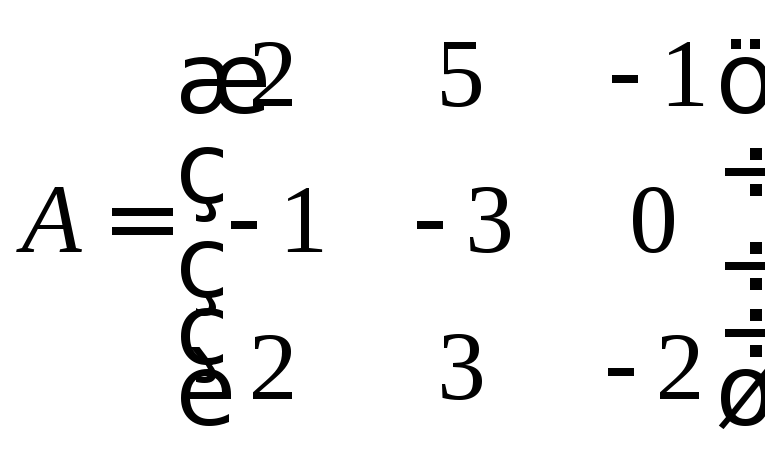 .
.
Розв’язок
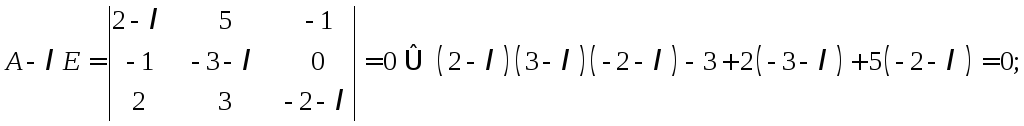

![]() — власні значення.
— власні значення.
Шукаємо власні вектори, що
відповідають власним значенням
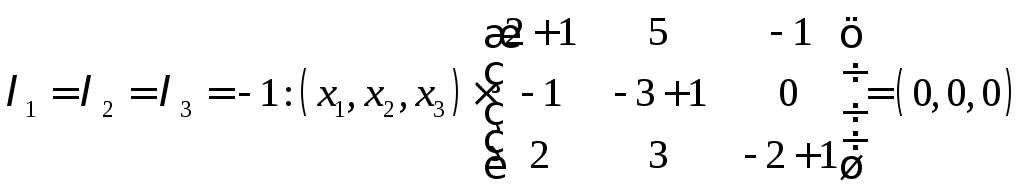 .
.

Ф.С.Р.:
![]()
![]() —власний вектор, що відповідає
власному значенню
—власний вектор, що відповідає
власному значенню
![]() .
.
б)
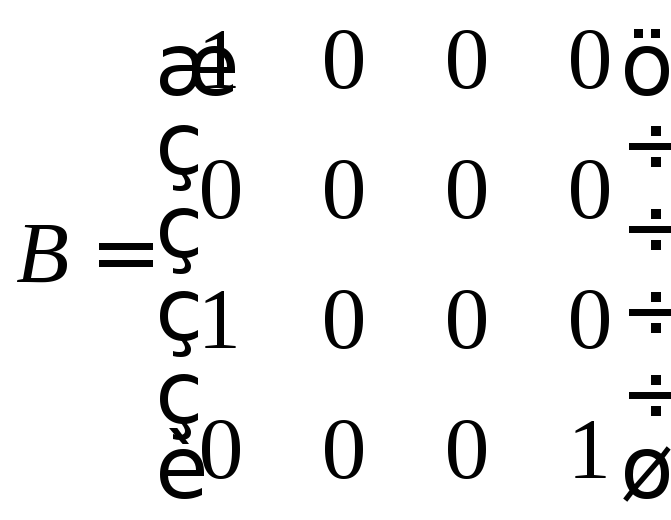
Розв’язок
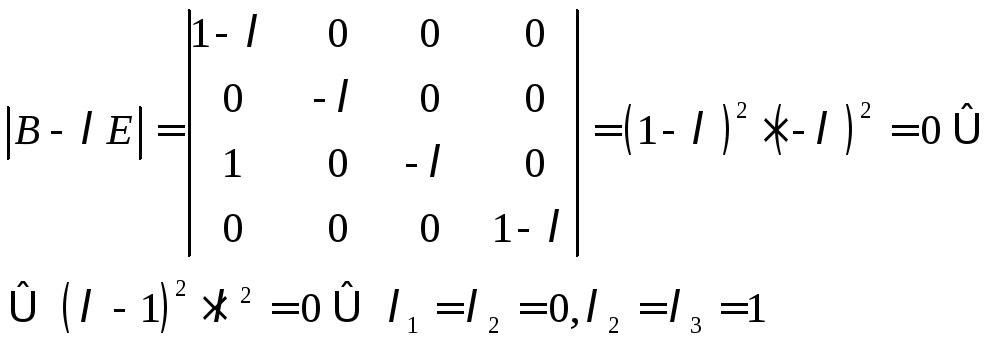
Шукаємо власні вектори, які
відповідають власному значенню

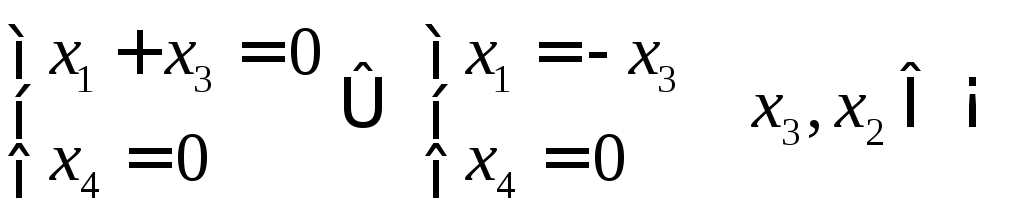
Загальний розв’язок:
![]()
Ф.С.Р.
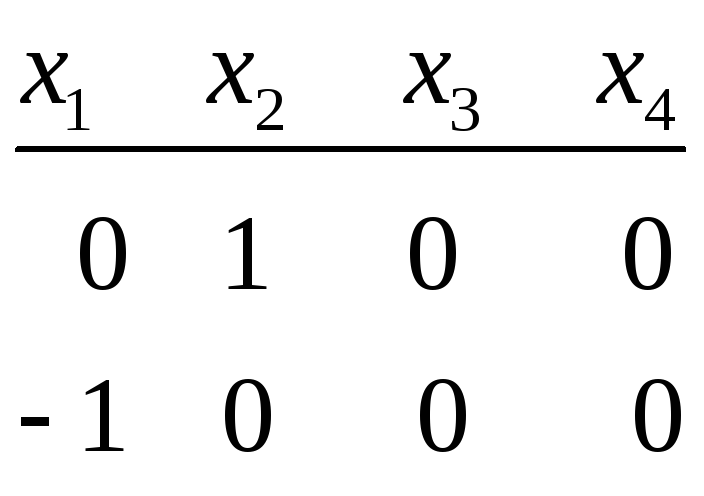
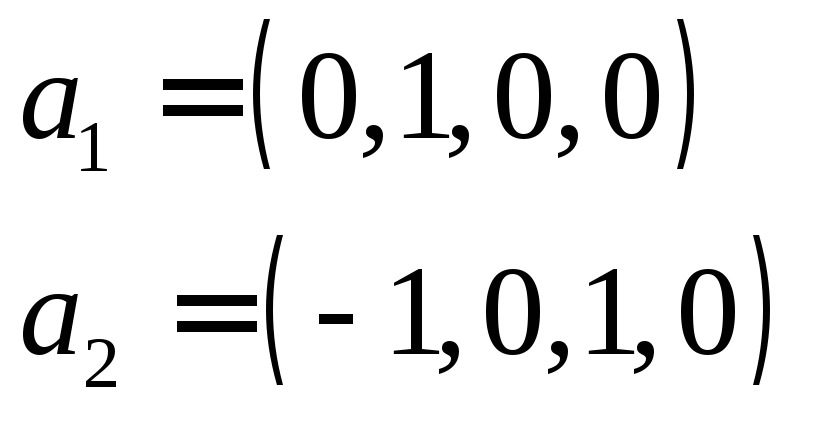 —власні вектори, що відповідають
власному значенню
—власні вектори, що відповідають
власному значенню
![]()
Шукаємо власні вектори, що
відповідають власні значення
![]()
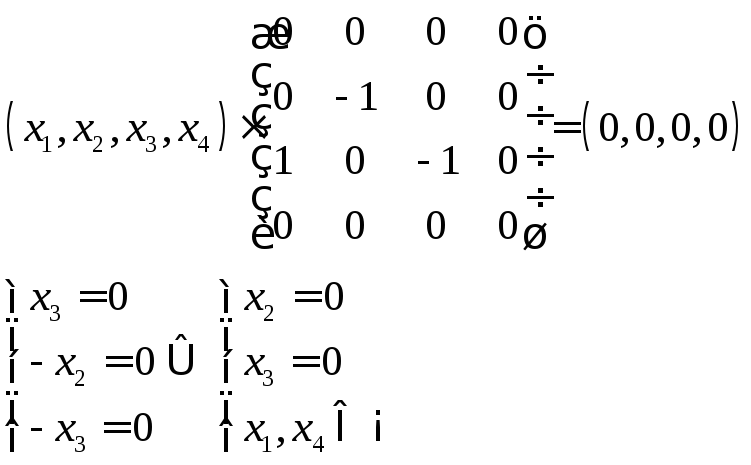
Загальний розв’язок:
![]()
Ф.С.Р.
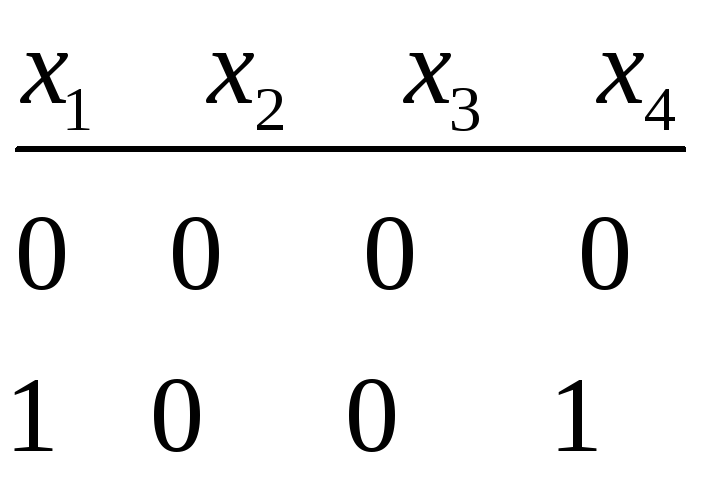
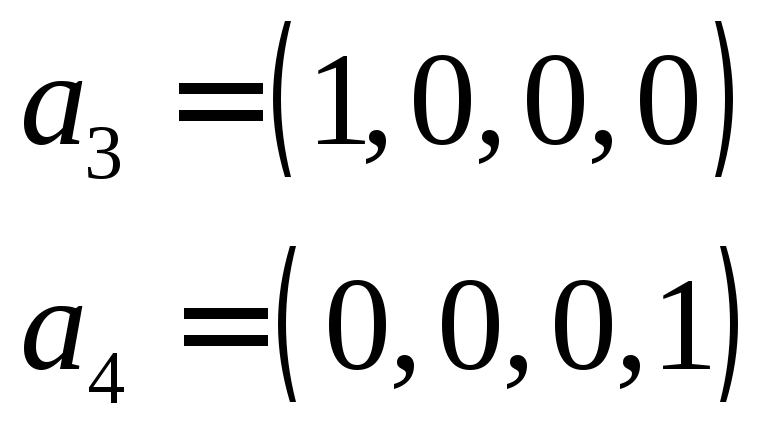 —власні вектори, що відповідають
власним значенням
—власні вектори, що відповідають
власним значенням
![]() .
.
в)
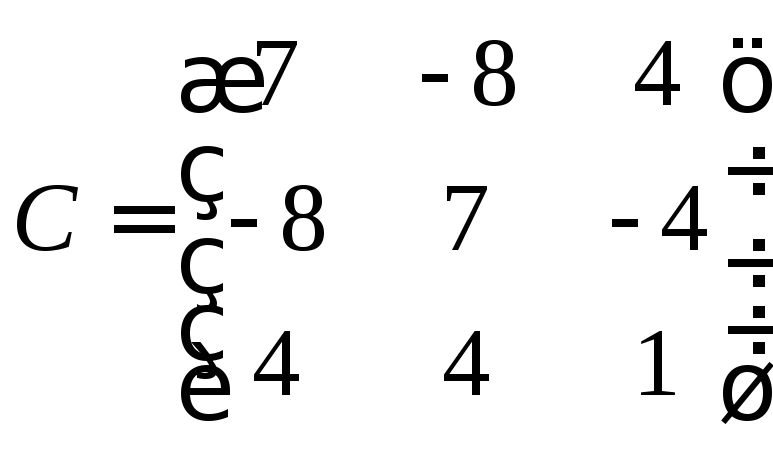
Розв’язок

![]()
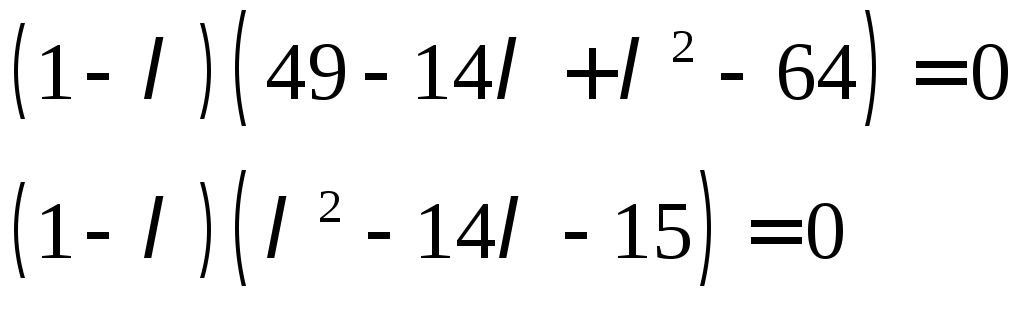

1) Шукаємо власний вектор, що
відповідає власному значенню
![]()

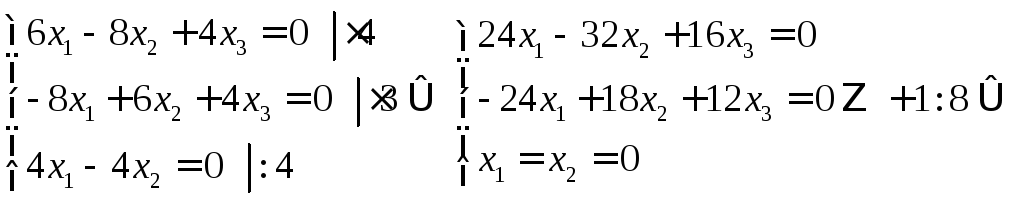
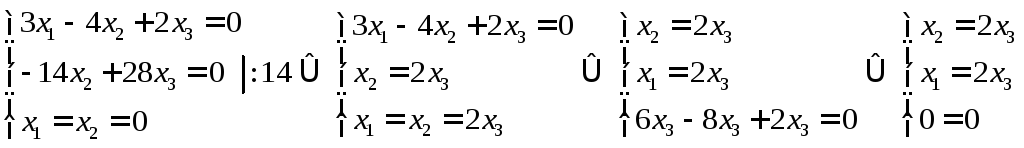
Загальний розв’язок:
![]()
![]() —власний вектор, що відповідає
власному значення
—власний вектор, що відповідає
власному значення
![]()
2)
![]()

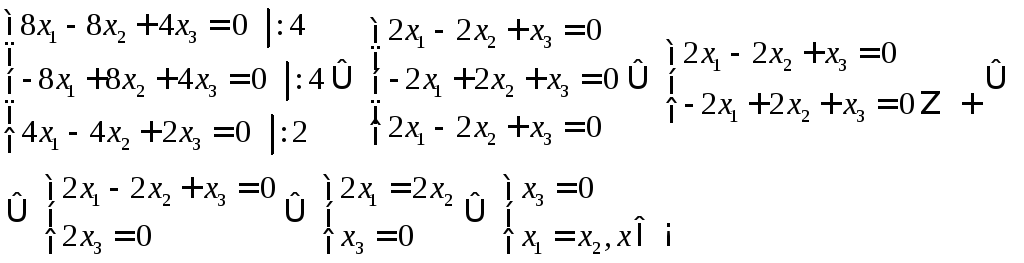
Загальний розв’язок системи
![]() .
Власний вектор
.
Власний вектор![]() — відповідний власному значенню
— відповідний власному значенню![]() .
.
3)
![]()
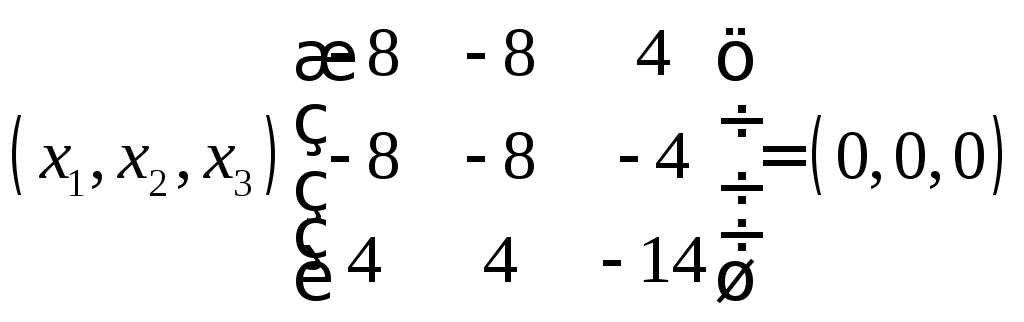

![]() загальний розв’язок системи
загальний розв’язок системи
![]()
Власне значення
![]() — йому відповідає власний вектор
— йому відповідає власний вектор![]() .
.
Відповідь:
![]()
![]()
![]()
