17. З’ясувати, які з наступних матриць можна звести до діагонального виду шляхом переходу до нового базису:
а)
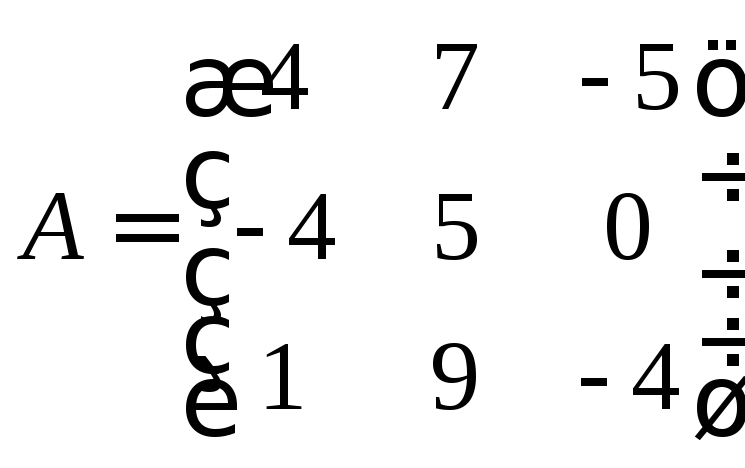 б)
б)
Розв’язок
Характеристичне рівняння:


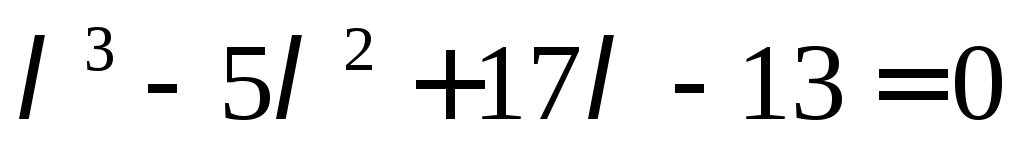
-
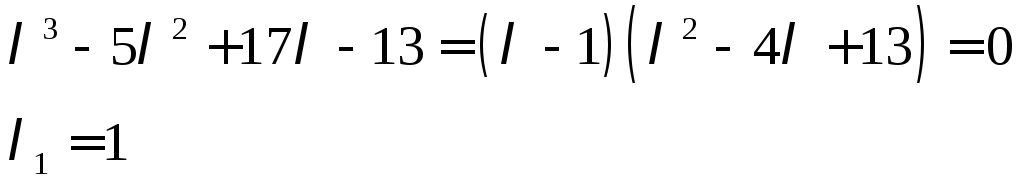
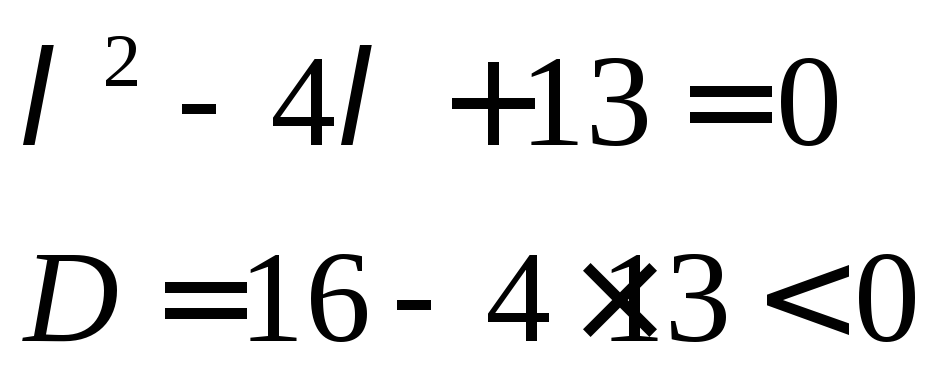
 —комплексні корені
характеристичного рівняння
—комплексні корені
характеристичного рівняння
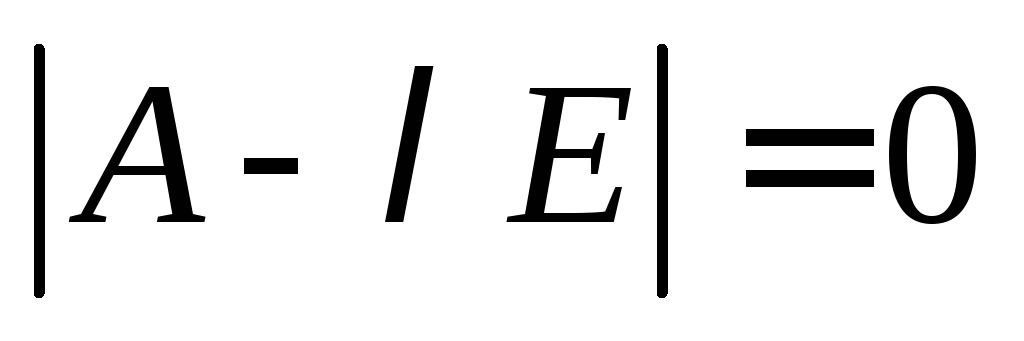 ,
тому не є власними значеннями оператора
,
тому не є власними значеннями оператора .
.
Шукаємо власні вектори, які
відповідають власному значенню
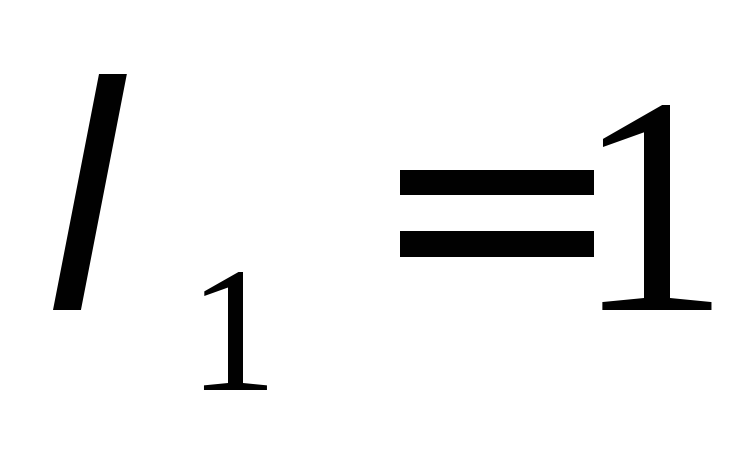 :
:
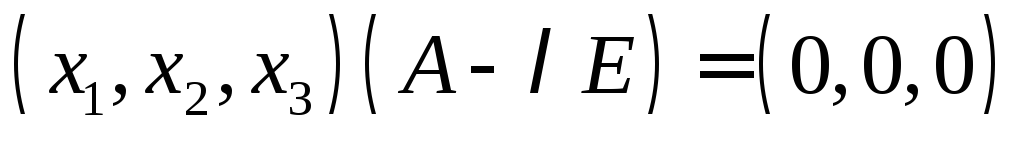
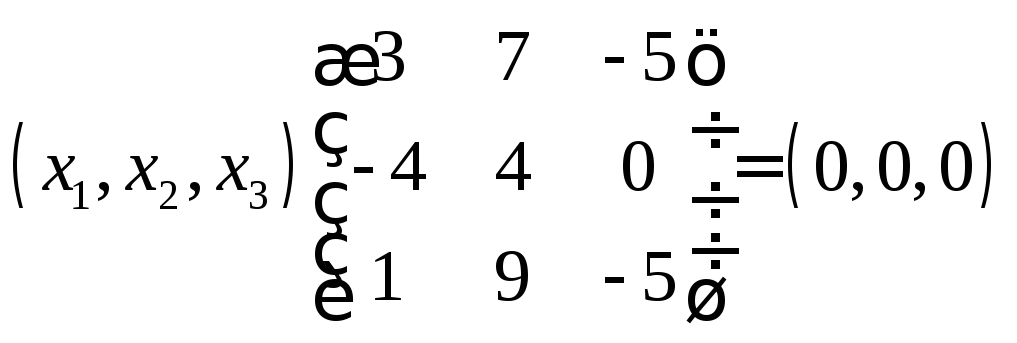
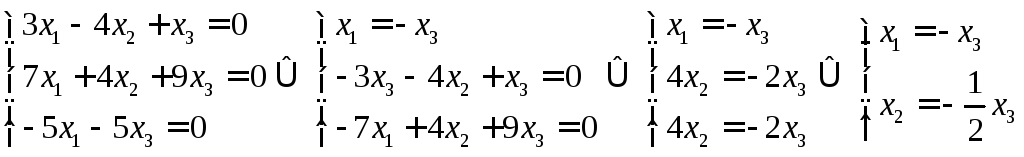
Загальний розв’язок:
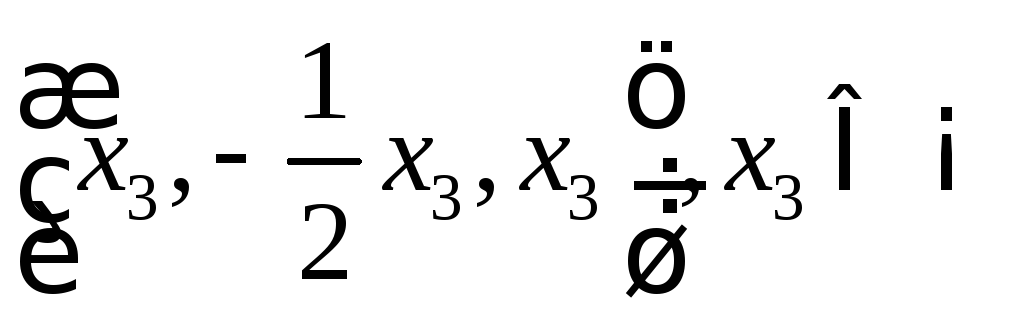
Власний вектор
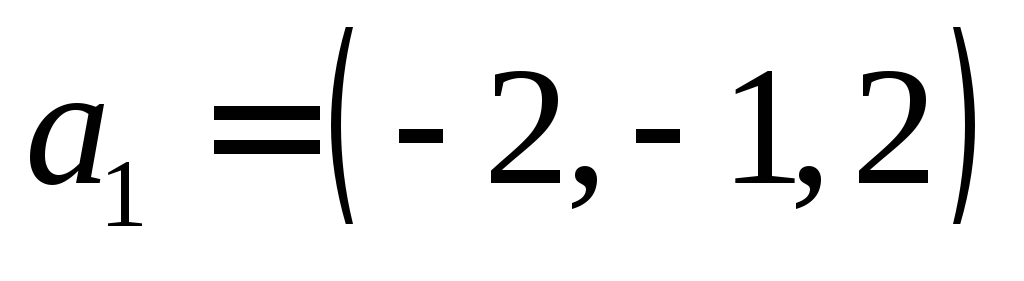 .
.
Оскільки власних векторів
оператора
 є лише один (тобто з них не можна побудувати
базис, в якому матриця оператора
є лише один (тобто з них не можна побудувати
базис, в якому матриця оператора буде діагональною), то матрицю
буде діагональною), то матрицю не можна звести до діагонального вигляду.
не можна звести до діагонального вигляду.
б)

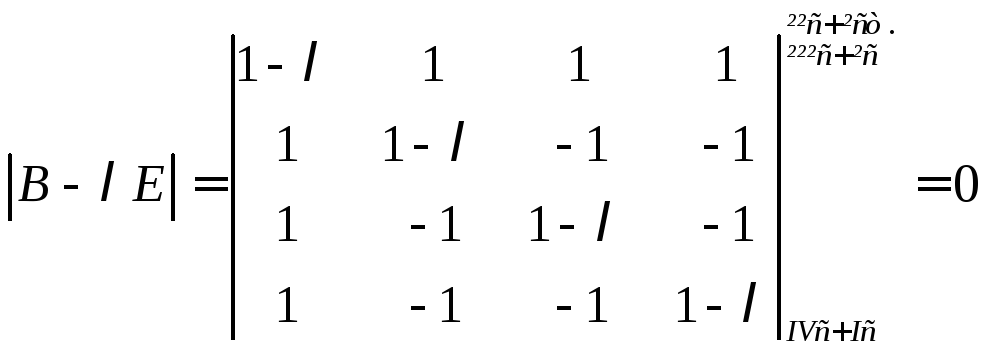

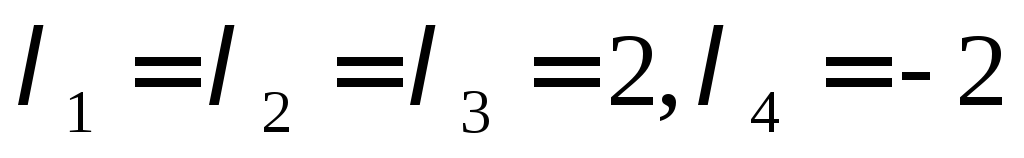
Шукаємо власні вектори, що
відповідають власному значенню
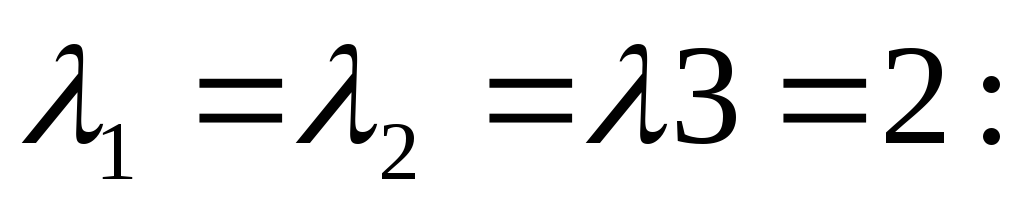
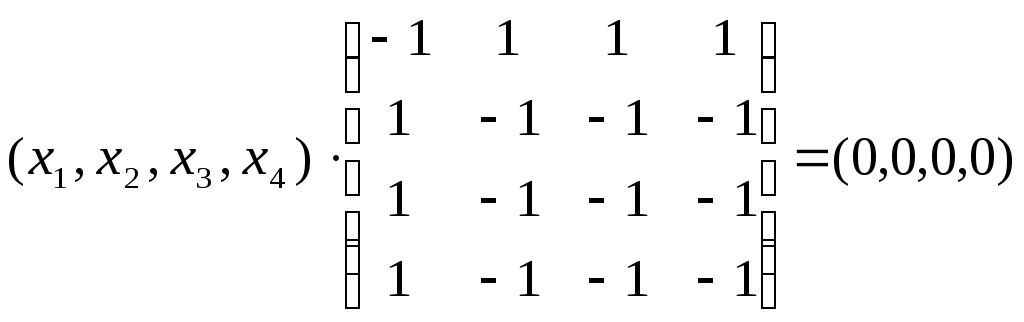
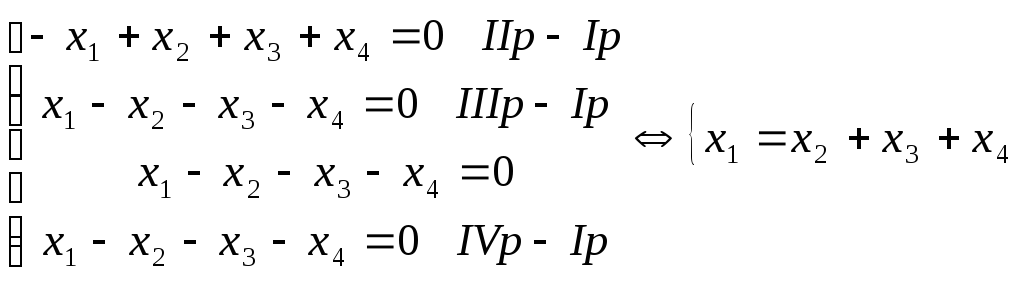
Загальний розв’язок системи

Ф.С.Р.
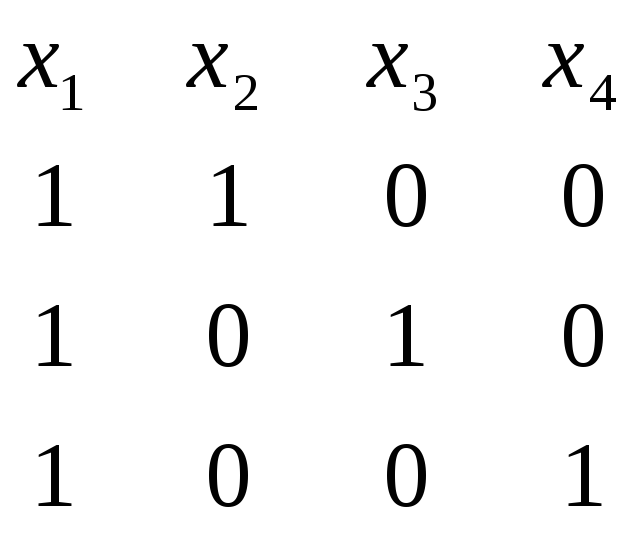
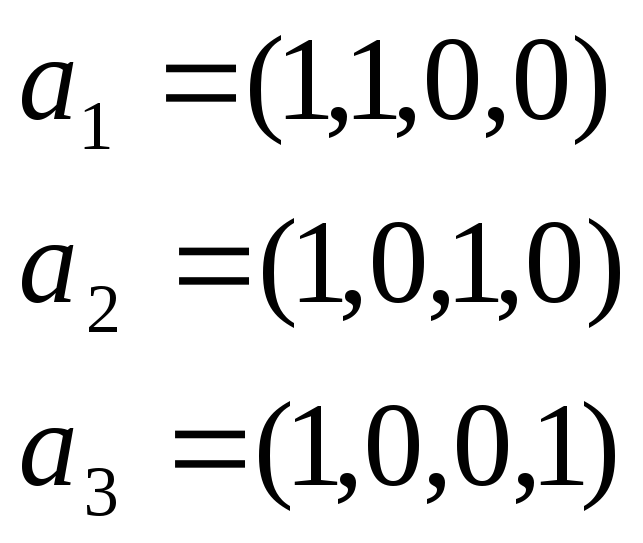 ‑власні вектори, що
відповідають вл. знач.
‑власні вектори, що
відповідають вл. знач.
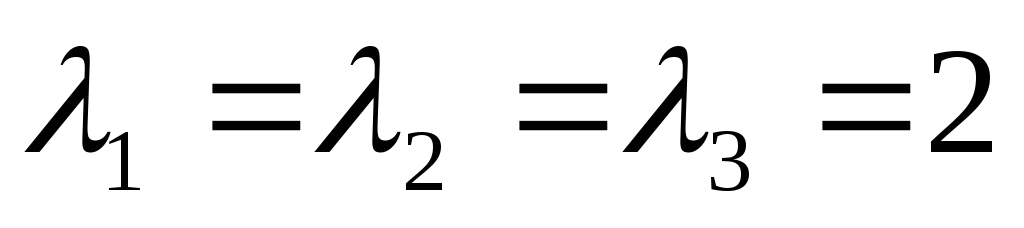
Шукаємо власні вектори, що
відповідають власному значенню
 .
.
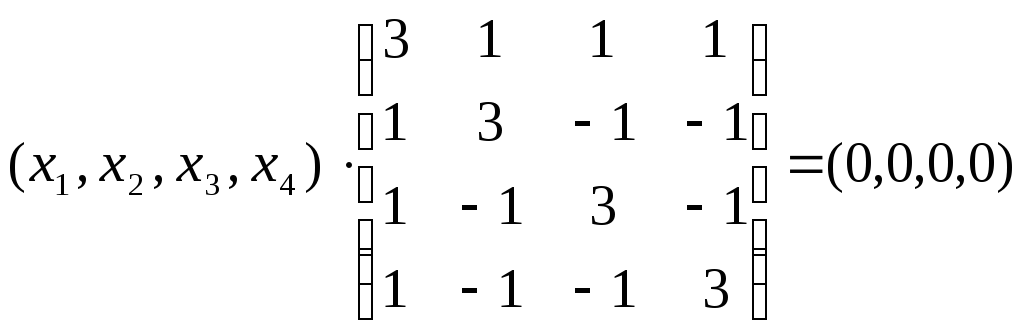
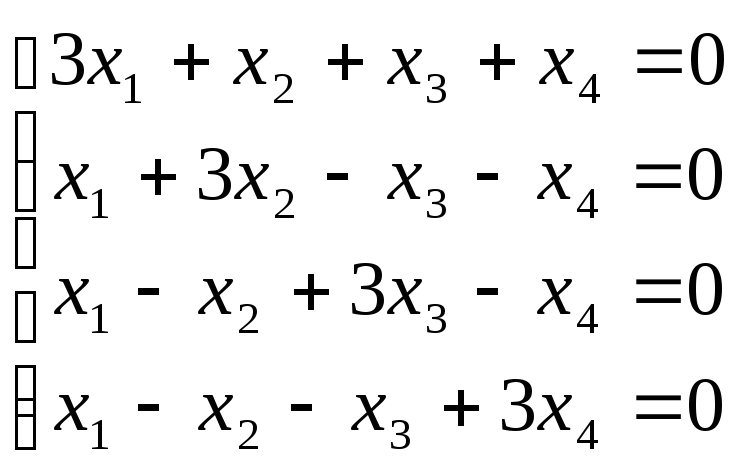

 ~
~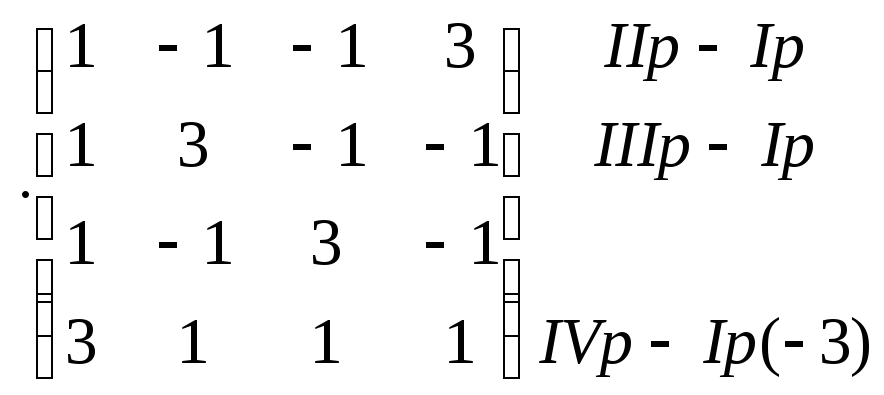 ~
~ ~
~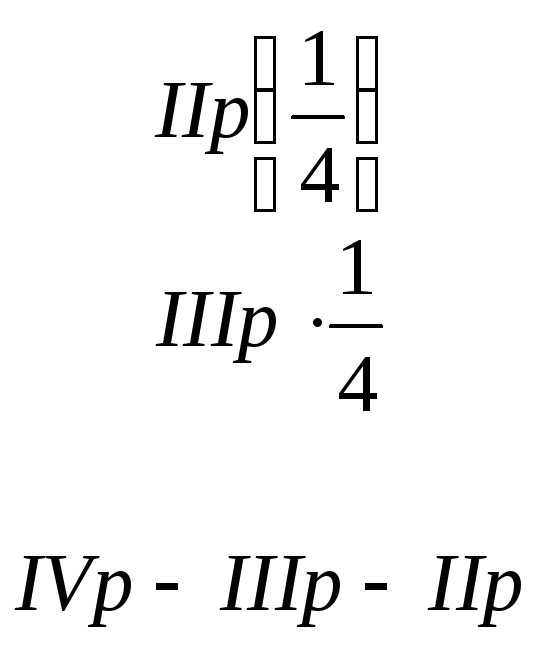 ~
~
~

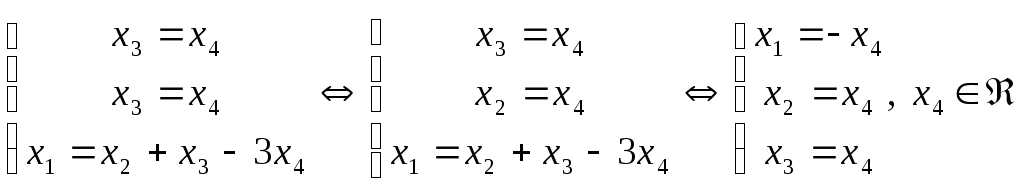
Загальний розв’язок системи:
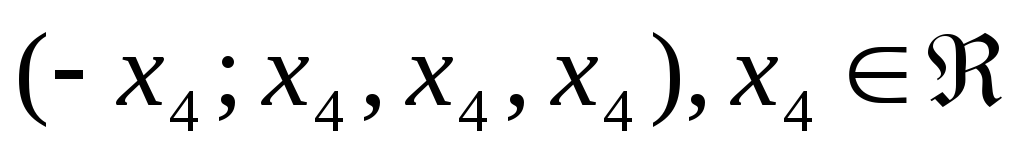
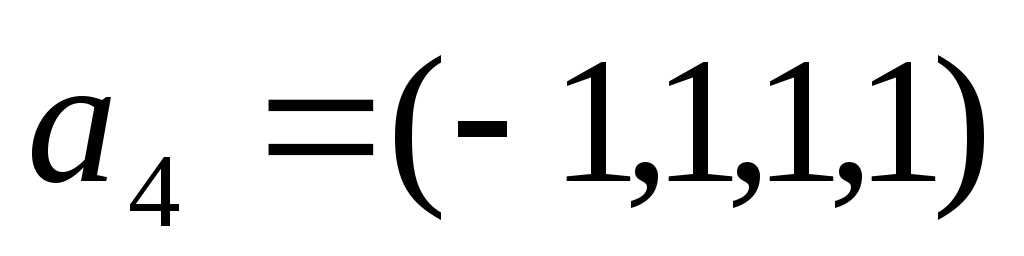 ‑власний вектор, що
відповідає власному значенню
‑власний вектор, що
відповідає власному значенню
 .
отже, оскільки із власних векторів
оператора
.
отже, оскільки із власних векторів
оператора можна побудувати базис
можна побудувати базис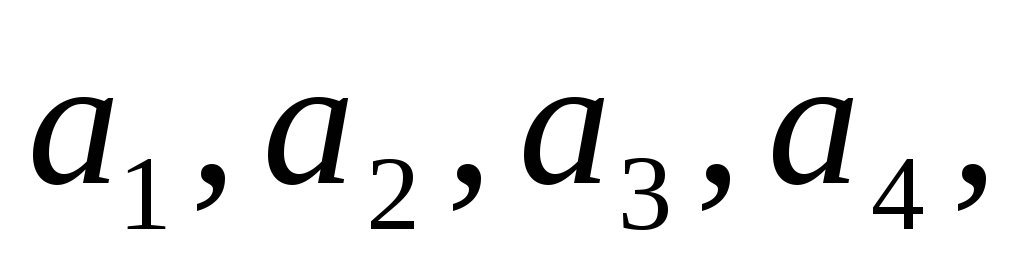 то в цьому базисі матриця оператора
то в цьому базисі матриця оператора
 буде подібна до діагональної
буде подібна до діагональної
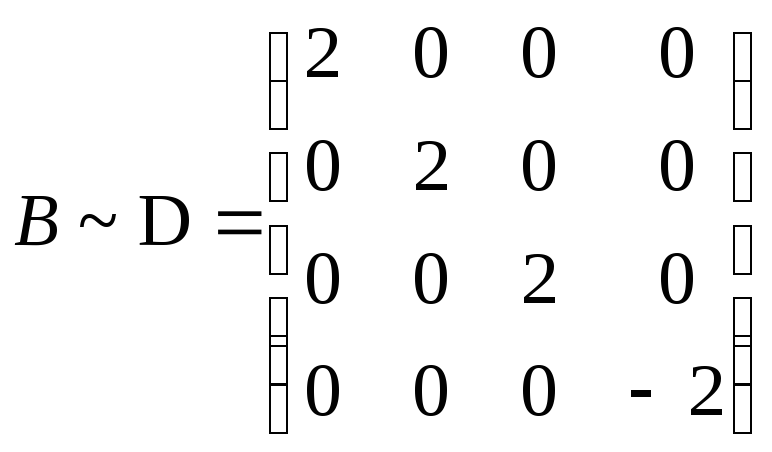 ‑матриця оператора
‑матриця оператора
 у базисі
у базисі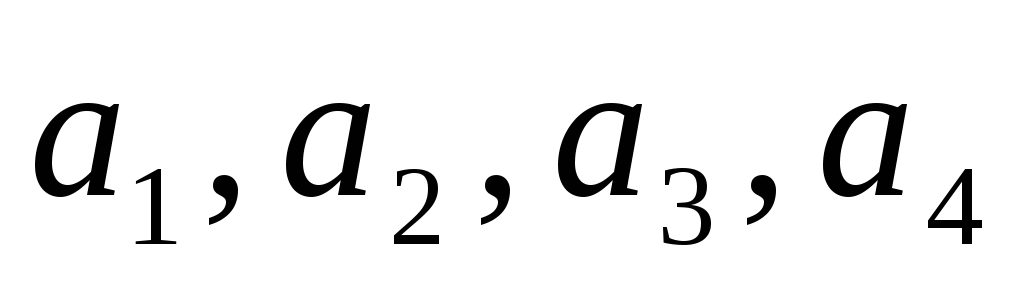
20


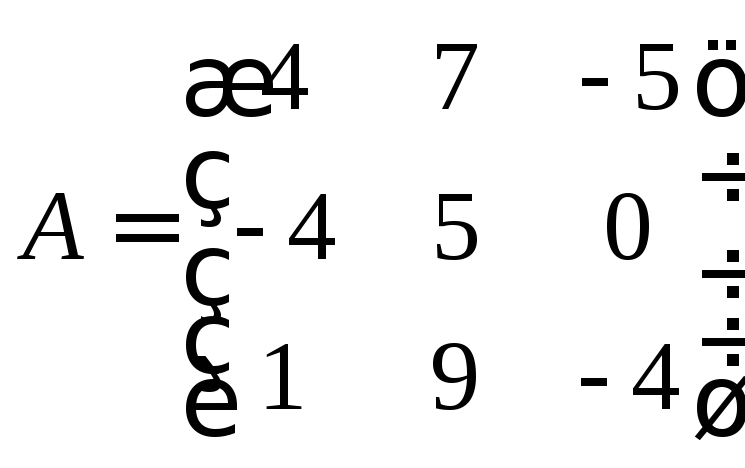 б)
б)

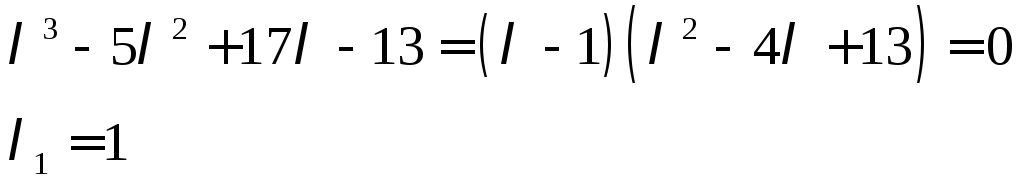
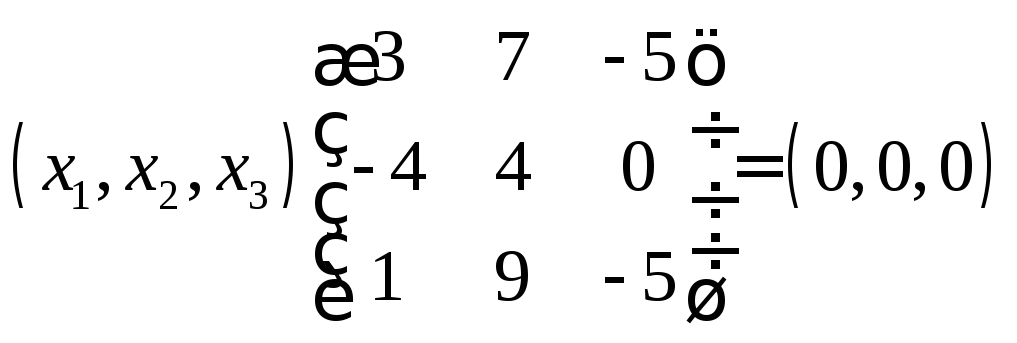
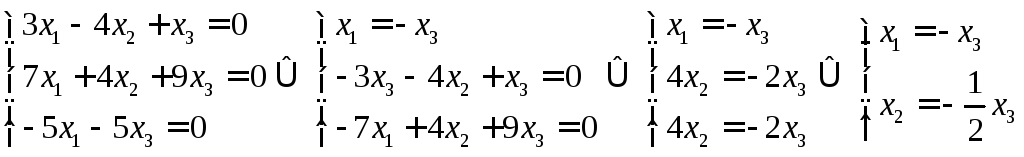

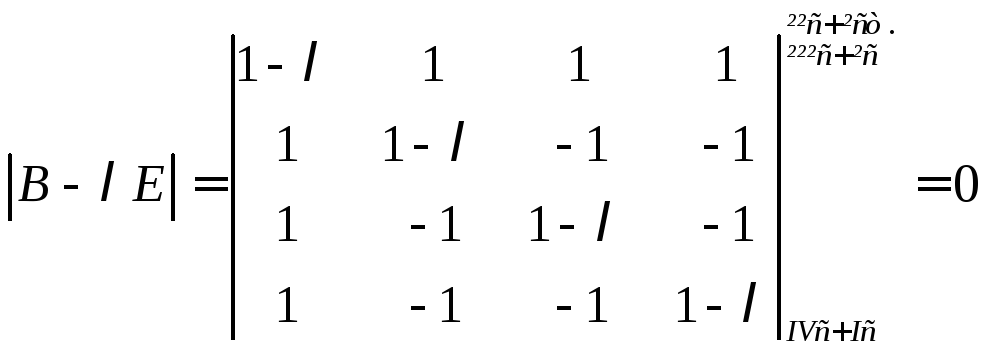


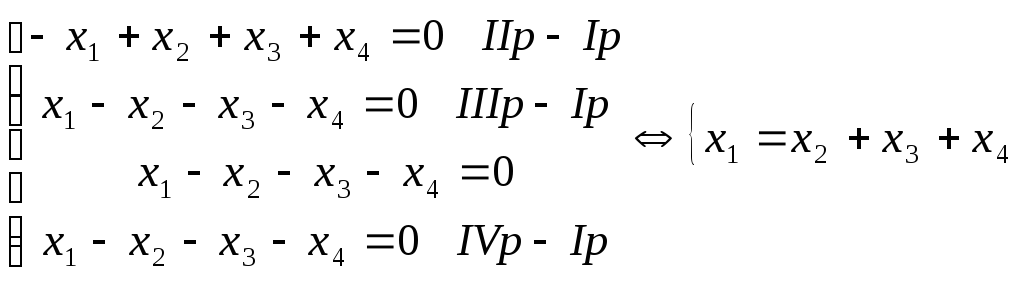
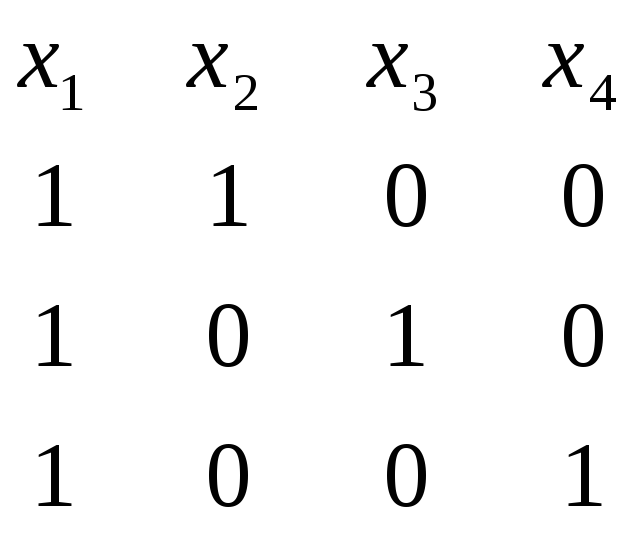
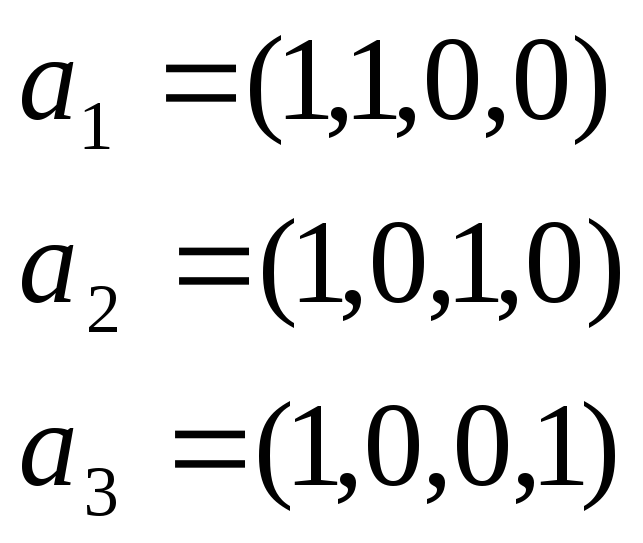 ‑власні вектори, що
відповідають вл. знач.
‑власні вектори, що
відповідають вл. знач.

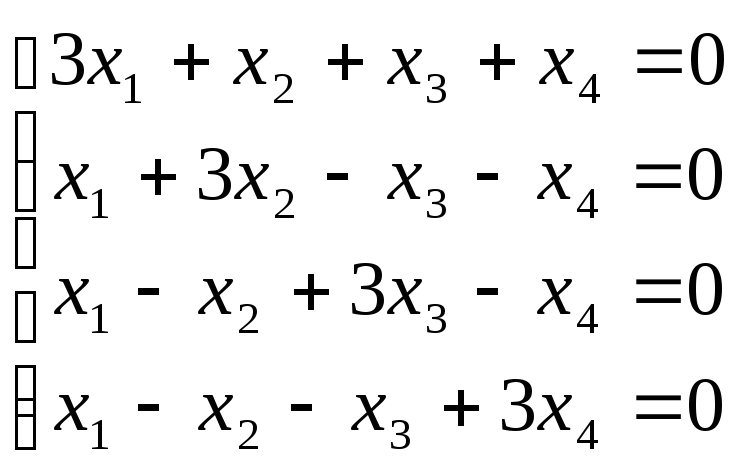
 ~
~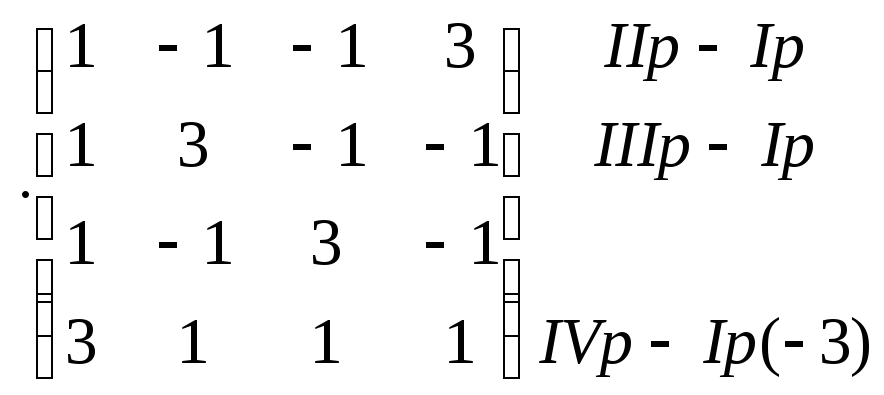 ~
~ ~
~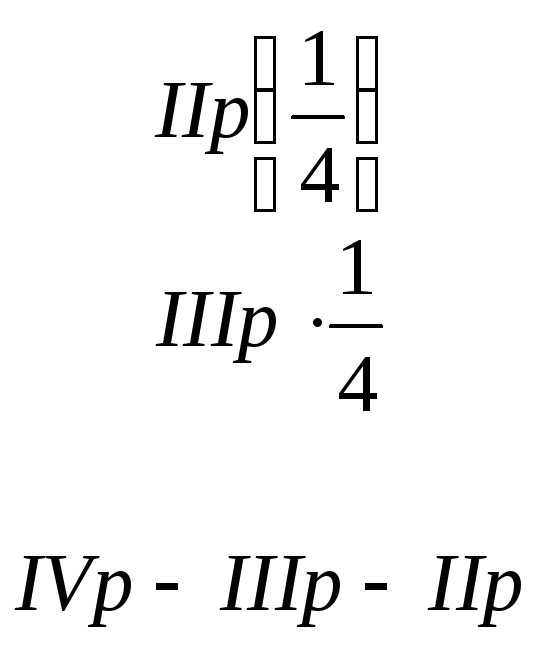 ~
~
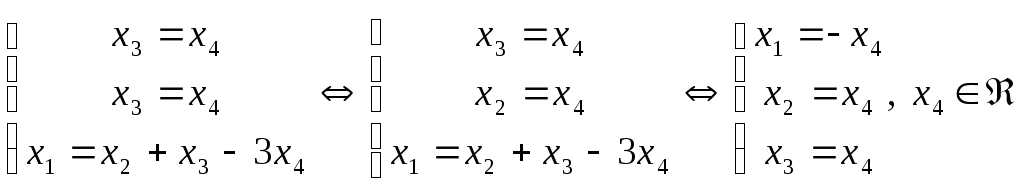
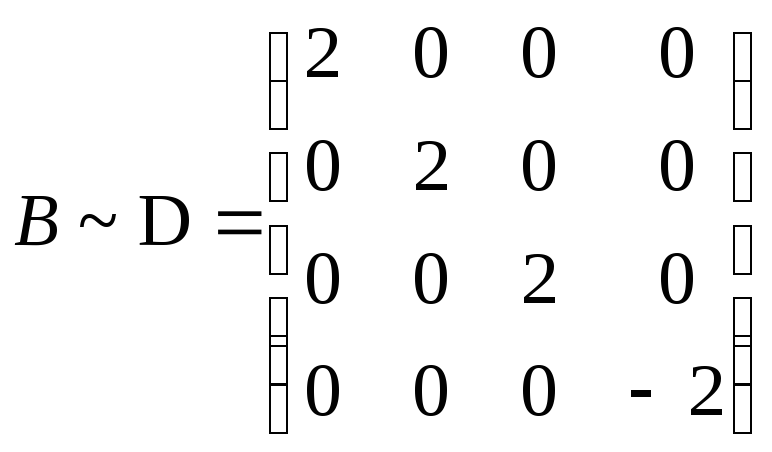 ‑матриця оператора
‑матриця оператора