
- •Лінійний простір. Аксіоматика. Ізоморфізм.
- •Скінченновимірні лінійні простори. Базис. Розмірність простору. Перетворення базису.
- •Підпростори лінійного простору. Їх сума та перетин.
- •Перетин (переріз) лінійних підпросторів.
- •Сума підпросторів лінійного простору.
- •Теорема про зв’язок між розмінностями суми і перерізу лінійних підпросторів.
- •Лінійні оператори. Їх властивості
- •Область значень та ядро лінійного оператора.
- •Власні значення і власні вектори лінійного оператора.
Область значень та ядро лінійного оператора.
Область значень лінійного оператора.
Нехай
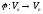 – лінійний оператор.
– лінійний оператор.
Означення
1:
Областю
значення (або
образом)
лінійного оператора
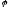 називається множина образів усіх
елементів простору
називається множина образів усіх
елементів простору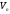 при дії оператора
при дії оператора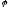 .
.
Область значень лінійного оператора позначають:
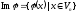
Твердження
1: Область
значень лінійного оператора є підпросторм
простору
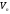 .
.
Дов.
Нехай
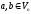 ,
тоді
,
тоді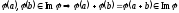
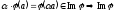 –підпростір
–підпростір
 .
.
Кожен підпростір має свою розмірність.
Означення
2: Розмірність
області значення лінійного оператора
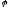 називаєтьсярангом
лінійного оператора.
називаєтьсярангом
лінійного оператора.
Тобто

Теорема
1:
Ранг
лінійного оператора
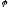 простору
простору
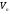 дорівнює рангу матриці А цього оператора
в деякому базисі.
дорівнює рангу матриці А цього оператора
в деякому базисі.
Дов.
Нехай
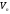 – лінійний простір;
– лінійний простір;
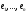 –база
цього простору.
–база
цього простору.
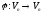 –лінійний
оператор.
–лінійний
оператор.
Розглянемо
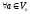 .
Тоді
.
Тоді
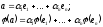
Оскільки
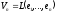 ,
то
,
то
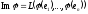
Простір
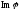 породжується векторами
породжується векторами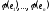 .
.
Тому
базою простору
 буде довільна лінійно незалежна
максимальна підсистема системи цих
елементів.
буде довільна лінійно незалежна
максимальна підсистема системи цих
елементів.
Тому
 з попереднього відомо, що
з попереднього відомо, що
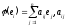 –елементи
матриці А
оператора
–елементи
матриці А
оператора
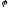 в базі
в базі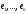 .
.
Звідси
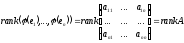
Ядро лінійного оператора.
Означення
3:
Ядром
лінійного оператора
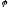 називається сукупність всіх тих елементів
з простору
називається сукупність всіх тих елементів
з простору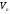 ,
які при дії
,
які при дії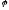 перетворюється в 0 (нульовий елемент
простору).
перетворюється в 0 (нульовий елемент
простору).
Ядро
лінійного оператора позначають
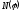 або
або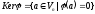
Твердження
2: Ядро
лінійного оператора є лінійним
підпростором простору
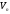 .
.
Доведення самостійно.
Означення
4: Розмірність
ядра лінійного оператора
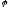 називаєтьсядефектом
лінійного оператора.
називаєтьсядефектом
лінійного оператора.
Приклад:
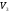 –простір
геометричних векторів простору, що
виходять з початку координат.
–простір
геометричних векторів простору, що
виходять з початку координат.
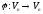 –проектування
векторів простору на вісь
–проектування
векторів простору на вісь
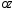 .
.
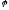 –лінійний
оператор (доводили подібне).
–лінійний
оператор (доводили подібне).
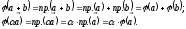
Побудуємо ядро і область значень цього оператора:
 –сукупність
векторів, що проектуються в нульовий
вектор – це всі вектори площини
–сукупність
векторів, що проектуються в нульовий
вектор – це всі вектори площини
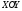 .
.
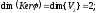
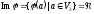 –це
вектори вісі
–це
вектори вісі
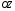 .
.
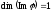
Отже,

Теорема рангу і зв’язок між рангом і дефектом лінійного оператора.
Теорема
2:
Сума
рангу і дефекта лінійного простору
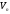 дорівнює
розмірності
дорівнює
розмірності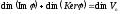
Дов. Позначимо
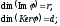
 .
.
Треба
довести, що
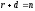
Нехай
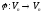 – лінійний оператор, база ядра якого
міститьd
векторів.
– лінійний оператор, база ядра якого
міститьd
векторів.
Нехай
 – база ядра
– база ядра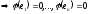
Доповнимо
цю базу векторами
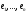 з простору
з простору до бази простору
до бази простору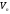 .
.
Тобто
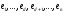 –база
–база
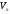 .
.
Розглянемо
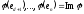
Для
цього покажемо, що довільний вектор
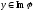 належить доU,
бо
належить доU,
бо
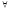 вектора зU
належить до
вектора зU
належить до
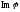 .
.
Дійсно,
нехай
 ,
тоді
,
тоді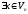 ,
такий, що
,
такий, що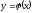 .
.
Оскільки
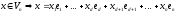 (*)
(*)
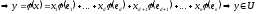 ,
отже
,
отже
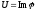
Залишилося
довести, що
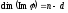 .
Для цього треба довести, що система
векторів
.
Для цього треба довести, що система
векторів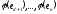 – лінійно незалежна. Будемо доводити
від супротивного.
– лінійно незалежна. Будемо доводити
від супротивного.
Припустимо,
що
 числа
числа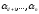 (одночасно не всі =0) такі, що
(одночасно не всі =0) такі, що
 (**)
(**)
Розглянемо
вектор
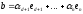 (***)
(***)
Очевидно,
що
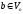
Знайдемо
його образ:
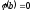 в силу (**)
в силу (**)
Це
означає, що
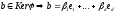 (****)
(****)
Записи
(***) і (****) означають, що для елемента
 існує два різні розклади по базі простору
існує два різні розклади по базі простору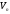 ,
що суперечить єдності розкладу вектора
по базі.
,
що суперечить єдності розкладу вектора
по базі.
Отже, припущення невірне і вектори:
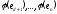 –лінійно
незалежні. Тому їх можна прийняти за
базу у
–лінійно
незалежні. Тому їх можна прийняти за
базу у
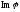
Отже,
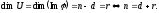
Зауваження: Різницю між порядком квадратичної матриці та її рангом називають дефектом матриці.
Отже, дефект лінійного оператора дорівнює дефекту його матриці.
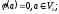
Нехай
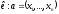 ,
тоді
,
тоді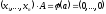 .
.
Не вироджений лінійний оператор.
Означення:
Лінійний
оператор
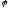 простору
простору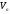 називаєтьсяне
виродженим, якщо
його ранг дорівнює розмірності простору:
називаєтьсяне
виродженим, якщо
його ранг дорівнює розмірності простору:
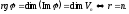
У протилежному випадку оператор називається не виродженим.
Для не вироджених лінійних операторів справедливі наступні твердження.
Твердження
1:
 .
.
Твердження
2:
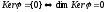 –
дефект не виродженого лінійного оператора
=0.
–
дефект не виродженого лінійного оператора
=0.
Твердження
3:
Якщо
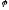 –
лінійний не вироджений оператор, то
різним векторам відповідають різні
образи:
–
лінійний не вироджений оператор, то
різним векторам відповідають різні
образи:
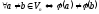
Дов.
Припустимо,
що
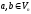 і
і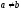 ,
але
,
але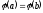
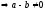 ,
але
,
але
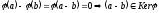 ,
але, згідно з твердженням 2 для не
виродженого лінійного оператора
,
але, згідно з твердженням 2 для не
виродженого лінійного оператора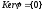 .
.
Отже,
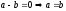 – суперечність.
– суперечність.
Твердження
4: Не
вироджений лінійний оператор
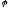 простору
простору
 є взаємно однозначним відображенням
цього простору на себе.
є взаємно однозначним відображенням
цього простору на себе.
Твердження
5:
Для
невиродженого лінійного оператора
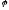 існує
обернений оператор
існує
обернений оператор
 ,
який
також є лінійним.
,
який
також є лінійним.
Дов.
Нехай

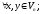
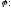
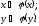
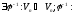
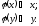
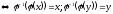
1)

2)
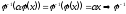 – лінійний оператор простору
– лінійний оператор простору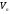
Зауваження: Кожне з цих можна прийняти за означенням невиродженого лінійного оператора.
Тоді решта тверджень випливають з нього.
Твердження 6: При дії невиродженого оператора лінійно незалежні вектори відображаються в лінійній залежності.
Самостійно
Дов.
Нехай
 – лінійно незалежна система векторів:
– лінійно незалежна система векторів:
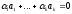 ,
де
,
де
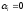 .
.
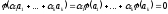
Оскільки,
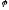 – не вироджена, то
– не вироджена, то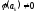 при
при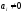 .
Коефіцієнти – ті ж самі:
.
Коефіцієнти – ті ж самі: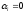 .
.
Отже,
система
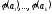 – лінійно незалежна.
– лінійно незалежна.
Висновок:
Лінійний
не вироджений оператор
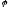 переводить будь-яку базу простору
переводить будь-яку базу простору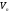 в деяку іншу базу цього простору.
в деяку іншу базу цього простору.
