Лінійні оператори. Їх властивості

П.1. Означення лінійного оператора.

Розглянемо лінійний простір і відображенняцього простору на себе, яке кожному векторуставить у відповідність цілком визначений векторпростору:

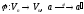
Відображення називаєтьсяперетворенням простору або оператором.

Елемент називаютьобразом елемента .

Отже,

Означення: перетворення просторуназиваєтьсялінійним оператором простору 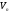, якщо воно задовольняє двом умовам:

1) – образ суми елементів = сумі образів.

2)

Приклади лінійного перетворення:

1. Нехай V – множина многочленів від х з дійсними коефіцієнтами степеня .

за правилом

1)

2)

Отже, – лінійний оператор.

2) –лінійний простір геометричних векторів простору.

–проекція векторів на вісь 0х.

– лінійний оператор, бо:

1)

2)

3) Нехай V – довільне лінійний простір;

а) – тотожне перетворення простору:

–лінійний оператор, який часто позначають .

б) – нульове перетворення простору:

–нульовий елемент простору V.

–лінійний оператор, його позначають .

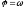Властивості лінійного оператора.

1) лінійний оператор простору переводить (відображає) довільну лінійну комбінацію

елементів в лінійну комбінацію

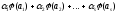їх образів з тими ж коефіцієнтами.

Дов. Знайдемо

Зауваження: відомо, що кожен вектор єдиним способом розкладається за елементами бази:

Отже, довільний лінійний оператор простору однозначно визначається заданням елементів

образів бази.

3. якщо – лінійний оператор простору , то:

Дов. 1) ,отже

2)

Матриця лінійного оператора.

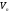Нехай – база лінійного простору і –лінійний оператор цього простору.

Подіємо оператором на кожен елемент бази. Отримуємо їх образи.

.

Які є елементами простору .

Їх можна розкласти за векторами бази:

(1)

або, скорочено,

Матрицю п-го порядку

називається матрицею лінійного оператора 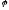в базі.

Матриця А складається з коефіцієнтів 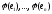по базису.

Порядок матриці А завжди співпадає з розмірністю простору .

У матричному вигляді рівність (1) записується так:

, де ,.

Висновок: Щоб знайти матрицю лінійного оператора в базідіємо операторомна кожен елемент бази і отримуємо образи, які розкладаємо за елементами бази. З коефіцієнтів розкладу складаємо матрицю А.

Приклад: У дійсному лінійному просторі многочленів степенярозглядаємо лінійний оператор

Знайти матрицю цього оператора а базі:

Зауваження: 1) Матриця лінійного оператора залежить від вибору бази.

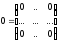
2) Нульовому оператору відповідає в довільному базисі нульова матриця:

4. Тотожному оператору відповідає одинична матриця

в довільному базисі.

4) Кожна матриця п-го порядку є матрицею деякого лінійного оператора простору в заданому базисі.

Координати базиса вектора.

Нехай – дійсний лінійний простір;– база цього простору.

Розглянемо довільний елемент .

Тоді (3)

–координати вектора а в базисі .

Розглянемо деякий лінійний оператор

Елемент . Тому його також можна розкласти за елементами бази.

(4)

де – координати образув базі.

Виникає питання про зв’язок між координатами а і його образу в базі.

З іншого боку:

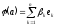(4)

Тому, враховуючи лінійну незалежність.

Елементів

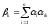(6)

У матричному вигляді маємо:

або, скорочено:

(7)

де А – матриця лінійного оператора .

Висновок: Рядок координат образу елемента в базідорівнює добутку рядка координат елемента а в базіна матрицю операторав цьому ж базисі.

Приклад: Вектор задано в базі,

Оператор в цій базі задано матрицею.

Знайти координати вектора в базі.

Розв’язання:

–?

Зв’язок між матрицями лінійного оператора в різних базах.

Ми вже зазначили, що матриця лінійного оператора залежить від бази. в різних базах один і той оператор визначається різними матрицями.

Виникає питання: чи існує зв’язок між цими матрицями і який це зв’язок?

Розглянемо лінійний простір і довільні дві бази в ньому:

між якими є зв’язок (8), деТ-матриця переходу від бази до.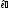

Нехай – лінійний оператор,

,

якому в базі відповідає матриця(9)

цьому ж оператору 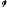в базівідповідає матриця

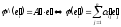(10)

Хочемо встановити зв’язок між матрицями А та:

1-ий спосіб:

(10)

(8)

Враховуючи, що вектори – лінійно незалежні, маємо:

(11)

Остання рівність записується в матричному вигляді так:

і

• зв’язок між матрицями оператора в різних базах.

2-ий спосіб:

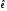–база ;

–база ;

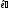–лінійний оператор.

Для формування деяких висновків наведемо означення:

Означення: дві квадратичні матриці А і В п-го порядку називається подібними, якщо існує не вироджена матриця Q така, що

У цьому випадку кажуть, що матриця А отримується із матриці В трансформуванням її за допомогою не виродженої матриці Q.

Зауваження:

1. якщо ~В, то В~А.

2. якщо ~В і В~С, то А~С.

3. квадратична матриці А подібна сама собі:

4. Подібні матриці мають однакові ранги.

Висновок: 1) Матриці А і , що задають один і той же лінійний оператор в різних базах – подібні.

2) Подібні матриці п-го порядку визначають один і той же оператор (лінійний) простору в різних базах.

Приклад: Розглянемо лінійний простір . Операторв базімає матрицю. Знайти його матрицю в базідо бази:

Розв’язання:

Приклад 2: оператор в базі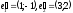має матрицю. Вектора в базі має координати.

а) Знайти матрицю оператора в базі.

б) Знайти координати вектора 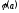в базі.