Побудова синусоїди

Синусоїдою називається плоска крива, яка графічно зображає зміну синуса в залежності від зміни його аргументу (кута).

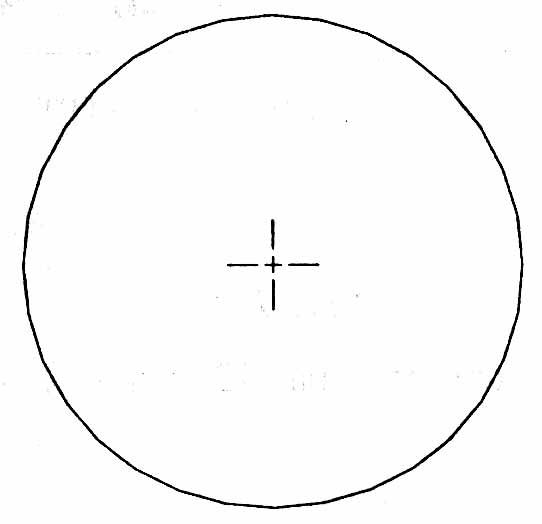
1. Для побудови синусоїди необхідно побудувати коло діаметром D (рис. 26), використовуючи команду CIRCLE (Коло).

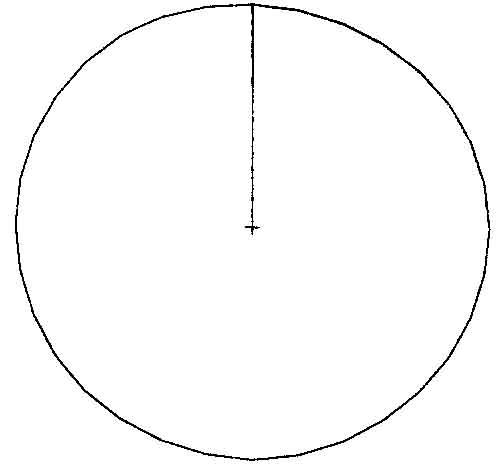
2. З центру кола командою LINE (Відрізок), використовуючи прив’язку Center (Центр), проводимо відрізок до верхньої квадрантної точки, використавши прив’язку Quadrant (Квадрант) (рис. 27).

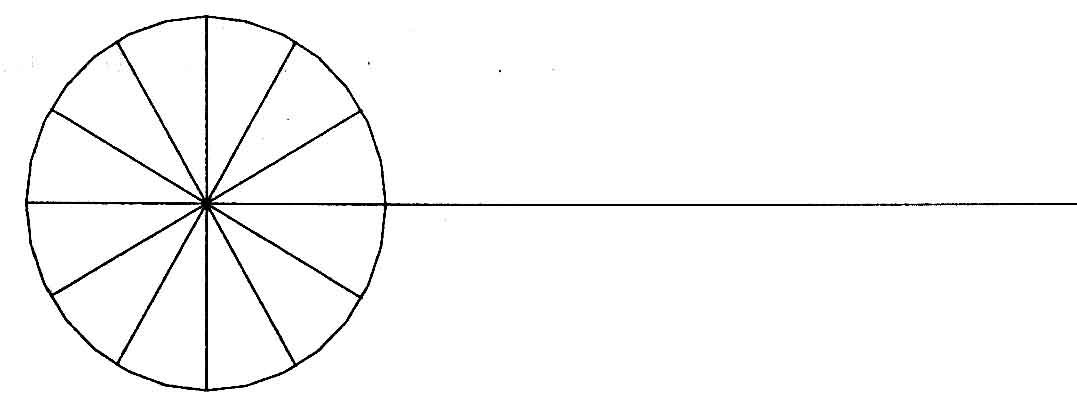
3. Ділимо коло на 12 рівних частин, використовуючи команду ARRAY (Масив) (рис. 28).

Рис. 26	Рис. 27	Рис. 28

4. На продовженні горизонтального діаметра будуємо відрізок довжиною , використовуючи команду LINE (Відрізок) і відносну систему координат (рис. 29).

5. Ділимо побудований відрізок на 12 рівних частин командою DIVIDE (Ділити) (рис. 30).

Рис. 29	Рис. 30

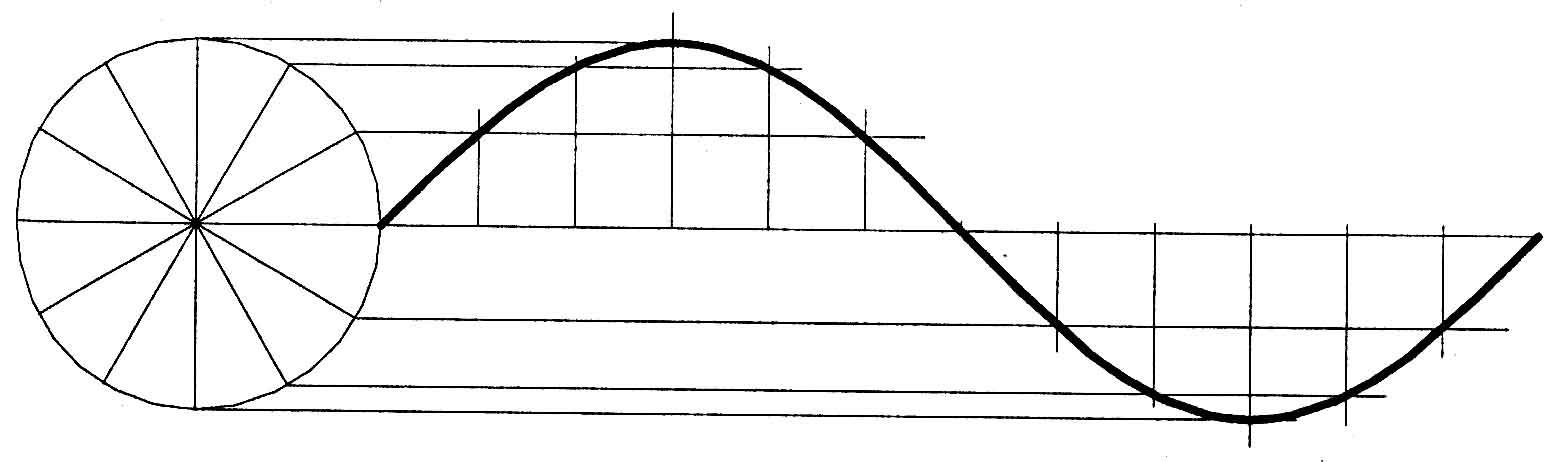
6. Використовуючи команду LINE (Відрізок) з включеним режимом ORTHO (Орто) (режим, при якому відрізки проводяться паралельно вісям координат), будуємо вертикальні і горизонтальні лінії як показано на рисунку 31.

7. Використовуючи команду SPLINE (Сплайн), послідовно з’єднуємо точки, отримані при перетині вертикальних і горизонтальних відрізків. Після цього отримаємо криву синусоїду. Для більш точної побудови використовується прив’язка Intersection (Перетин) (рис. 32).

Рис. 31	Рис. 32

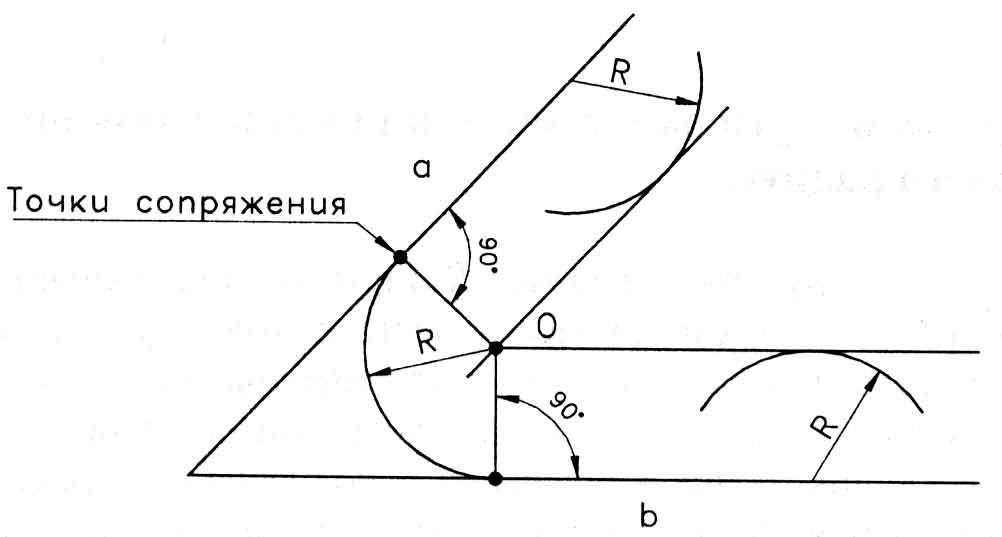
Сполучення прямих ліні, що перетинаються, за допомогою дуги

Для побудови сполучення двох прямих і, що перетинаються, під гострим кутом дугою заданого радіусуR необхідно визначити геометричне місце центрів кіл, які віддаленні від прямих на відстань R. Для цього на відстані R проводять прямі, що паралельні заданим, до перетину в точці О (рис. 33).

Дуга радіусу R, яка проведена з точки О, як з центра, і буде дугою сполучення (рис. 34). Основа перпендикулярів, які опущенні з точки О на прямі ібудуть точками сполучення.

Рис. 33	Рис. 34

Побудова сполучення двох прямих, що перетинаються під тупим кутом дугою заданого радіусу R (рис. 35) виконується по аналогії з попереднім.

Рис. 35

Побудова вище описаних сполучень розглянемо на прикладі сполучень двох прямих і, що перетинаються.

1. Вибираємо команду FILLET(Сполучення).

2. На питання команди:

Select first object or [Polyline/Radius/Trim]:

Вводимо ключ R.Enter.

3. На наступний запит системи:

Specify fillet radius <20.0000>:

Необхідно указивати величину радіусу сполучення. Enter. На цьому дія команди завершується.

4. Натискаємо Enter, повторно викликаємо командуFILLET.

5. На запит команди:

Select first object or [Polyline/Radius/Trim]:

Указиваємо одну з прямих сполучення, наприклад .

6. На наступне питання системи:

Select second object:

Вказуємо другу пряму сполучення . Після цього отримаємо необхідне нам спряження.

Сполучення дуги кола і прямої за допомогою дуги заданого радіусу

Сполучення дуги кола радіусу Rі прямої виконують наступним чином. Спочатку визначають геометричне місце центрів дуг сполучення радіусомR1. Для цього на відстані R1 від прямої проводять паралельну їй прямуm, а з центру О радіусом R+R1 – дугу концентричного кола. Точка О1 буде центром дуги сполучення. Точка С отримана на перпендикулярі, який проведений з точки О1 до прямої , а точка В – на прямій, яка з’єднує точки О і О1 (рис. 36).

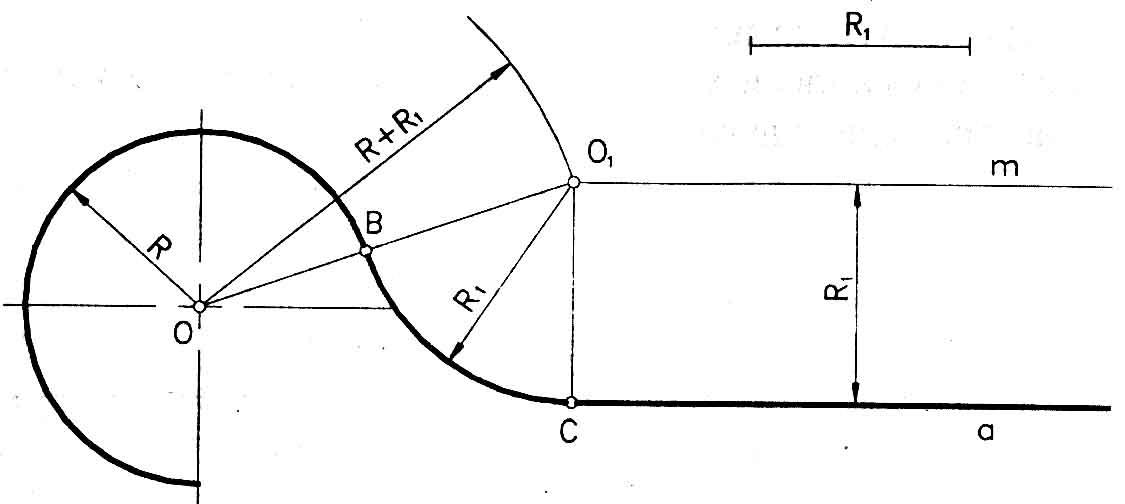
Рис. 36