2.Перетворення задачі з неоднорідними граничними умовами до задачі з однорідними граничними умовами.

1.Розглянемо задачу про поширення тепла в теплоізольованому стержні, на кінцях якого підтримується постійна температура і, тобто маємо рівняння у частинних похідних:

, (2.1)

крайові умови:

і початкові умови:

Труднощі цієї задачі полягають у тому, що оскільки крайові умови неоднорідні, то не можна розв’язувати її методом поділення змінних. Але очевидно, що при t розв’язок задачі наближається до стаціонарного, яке лінійно змінюється (вздовж осі OX) від температури K₁ до температури K₂. Інакше припустимо, що температуру у цій задачі можна подати у вигляді суми двох доданків: стаціонарного (граничного розв’язку для великих значень аргументу t) і перехідного, тобто частини розв’язку, яка залежить від початкових умов і зі збільшенням змінної t наближається до нуля, або

(2.2)

У цьому випадку ставиться задача знаходження перехідної температури . Припустимо, що функціязадовольняє однорідним граничним умовам:

(2.3)

Підставимо (2.2) у граничні умови задачі (2.1). Враховуючи (2.3), знайдемо величини А і В. Тепер задачу (2.1) можна розв’язати відносно нової невідомої функції V(x,t) і додати її до стаціонарного розв’язку. Отже в результаті одержимо шукану функцію V(x,t). Оформлюємо задачу відносно функції V(x,t). Для цього функцію (2.2) підставимо в рівняння та у граничні та початкові умови, тоді нова задача буде:

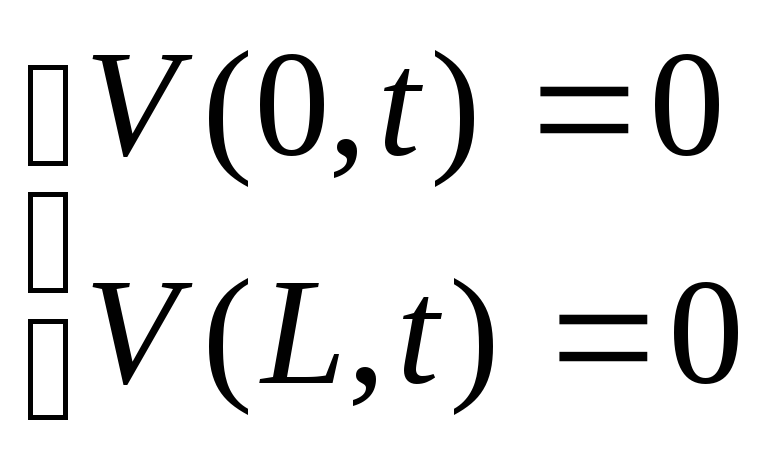
Таким чином, одержали задачу не тільки з однорідним рівнянням, а й з однорідними граничними умовами, що дозволяє розв’язати її методом поділення змінних.

2.Перетворення неоднорідних граничних умов, які залежать від змінної t, в однорідні.

Розглянемо типову задачу:

(2.4)

Для перетворення цих граничних умов у нульові виберемо розв’язок задачі у такій формі:

, (2.5)

де функції A(t) та B(t) вибирають такими, щоб

(2.6)

задовольняло неоднорідним граничним умовам задачі (2.4). у цьому випадку функція V(x,t) буде задовольняти аналогічним, тільки однорідним, граничним умовам.

Підстановка функції S(x,t) у граничні умови

зводить до двох рівнянь, з яких можна визначити A(t) і B(t).

В результаті отримаємо

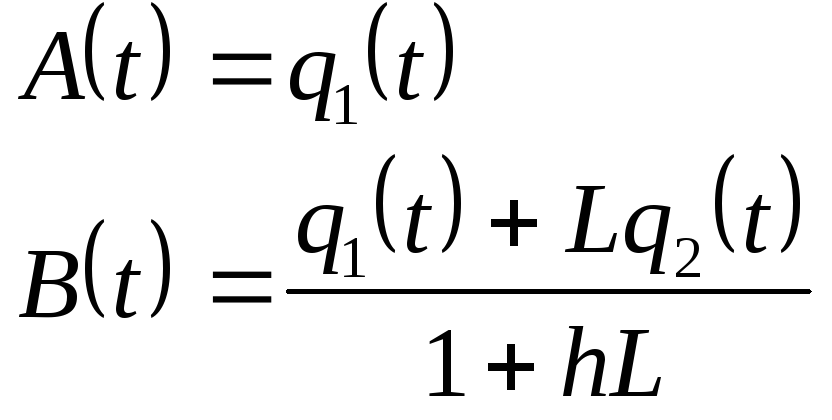(2.7)

Отже,

+(2.8)

Якщо підставити вираз (2.8) для U(x,t) в рівняння, граничні та початкові умови задачі (2.4), то одержимо нову задачу для невідомої функції V(x,t):

- неоднорідне рівняння у частинних похідних

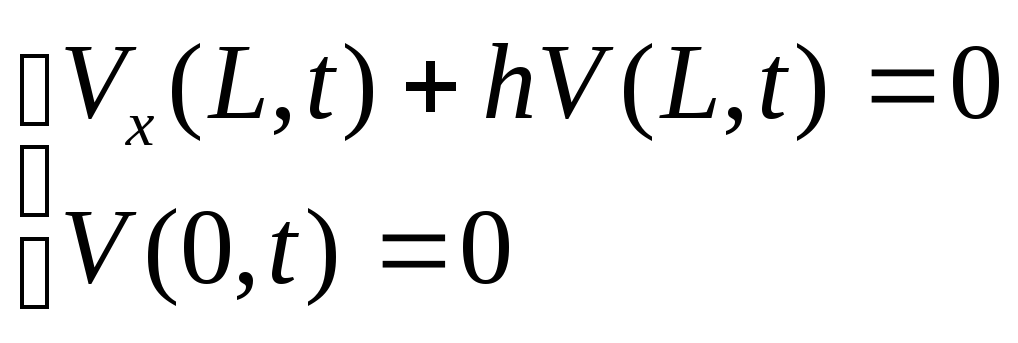- однорідні граничні умови

- початкові умови

Маємо нову задачу з однорідними граничними умовами, але рівняння стало неоднорідним. У цьому випадку задачу можна розв’язати методом інтегральних перетворень або скористатися розвиненням у ряд по власним функціям.

Зауваження:

1.Лінійні неоднорідні граничні умови загального виду

також можна перетворити в однорідні граничні умови. Очевидно, що нове рівняння, в цьому випадку, буде неоднорідним.

2.Деякі методи розв’язку задач не мають ніяких вимог до однорідності граничних умов, отже, у такому випадку, не треба їх і перетворювати в однорідні.