
- •Розв’язок деяких задач математичної фізики методом поділення змінних. Методичні вказівки до виконання типового завдання з дисципліни
- •1.Виведення рівняння теплопровідності.
- •В результаті одержимо наступне рівняння
- •2.Перетворення задачі з неоднорідними граничними умовами до задачі з однорідними граничними умовами.
- •2.Перетворення неоднорідних граничних умов, які залежать від змінної t, в однорідні.
- •3.Метод поділення змінних. (Метод Фур’є).
- •3.1.Загальні принципи метода поділення змінних.
- •3.2.Поділення змінних у задачі теплопровідності стержня з теплоізольованою бічною поверхнею.
- •3.3.Знаходження розв’язків, які задовольняють граничним умовам.
- •3.4. Пошук розв’язку, який задовольняє рівнянню, граничним та початковим умовам.
- •Якщо підставити (3.8) у (3.7), то будемо мати
- •4. Поширення тепла у стержні.
- •Процес поширення тепла у стержні описується рівнянням
- •Враховуючи, що
- •5. Виведення рівняння поперечних коливань струни. Будемо розглядати рівняння
- •6.Повздовжні коливання стержня або поперечні коливання струни.
- •7. Стаціонарний розподіл тепла у платівці. (Задача Діріхлє у прямокутнику для рівняння Лапласа).
- •Крайові задачі для рівнянь еліптичного типу.
- •9. Метод граничних елементів.
- •Враховуючи отримані формули, маємо
3.Метод поділення змінних. (Метод Фур’є).
Сутність методу – розклад шуканого розв’язку на добуток найпростіших компонент.
Метод поділення змінних вживається у таких випадках:
1.Рівняння лінійне й однорідне (не обов’язково з постійними коефіцієнтами).
2.Граничні умови задаються у вигляді:
![]() ,
,
де
![]() – константи (такі граничні умови
називаються лінійними однорідними ).
– константи (такі граничні умови
називаються лінійними однорідними ).
3.1.Загальні принципи метода поділення змінних.
Для найпростішого рівняння з частинними похідними поділення змінних – це пошук розв’язку у вигляді:
![]()
де X(x) – функція, залежна від змінної х;
T(t) – функція, залежна від змінної t.
Необхідно знайти
нескінченне число таких розв’язків
рівняння з частинними похідними, які
задовольняють граничним умовам. Ці
найпростіші функції
![]() називаються фундаментальними розв’язками.
називаються фундаментальними розв’язками.
Розв’язок задачі
U(x,t)знаходиться у вигляді лінійної комбінації
фундаментальних розв’язків![]() тобто вислідна суми
тобто вислідна суми
![]()
яка задовольняє початковим умовам. І оскільки ця сума задовольняє рівнянню і граничним умовам, вона є розв’язком вихідної задачі.
3.2.Поділення змінних у задачі теплопровідності стержня з теплоізольованою бічною поверхнею.
Знайти функцію U(x,t), яка є розв’язком задачі
![]() (3.1)
(3.1)
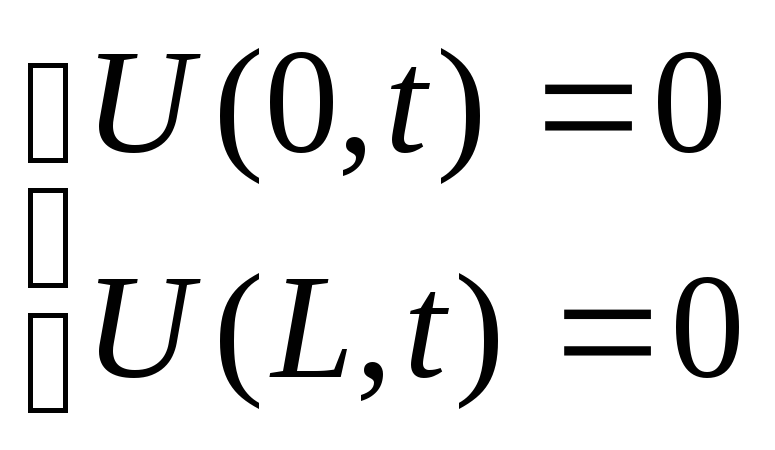 (3.2)
(3.2)
![]() (3.3)
(3.3)
де
![]() – постійна
величина.
– постійна
величина.
Будемо шукати розв’язок у вигляді:
![]() (3.4)
(3.4)
Підставимо (3.4) в рівняння (3.1), одержимо:
![]()
Поділимо
обидві частини останнього рівняння на
![]()
![]()
У цьому виразі змінні поділені, тобто ліва частина рівняння залежить від t, а права – тільки від x. І оскільки x і t незалежні одне від одного, то кожна частина цього рівняння повинна бути константою. Позначимо її через k, тоді
![]()
![]()
або
![]()
Тепер можна розв’язати кожне з цих звичайних диференціальних рівнянь. Добуток відповідних розв’язків буде задовольняти вихідному рівнянню з частинними похідними.
Слід
звернути увагу на ту обставину, що
константа k
повинна бути від’ємною
(у протилежному випадку рівняння
![]() з граничними умовамиX(0)=0
і X(L)=0
має тільки розв’язок X(x)=0,
тобто функція T(t)
повинна наближатися до нуля при t
з граничними умовамиX(0)=0
і X(L)=0
має тільки розв’язок X(x)=0,
тобто функція T(t)
повинна наближатися до нуля при t![]() ).
).
Виходячи
з цього, позначимо![]() ,
де
,
де![]() не може дорівнювати нулю, оскільки тоді
розв’язок
буде тривіальним. Отже вираз “-
не може дорівнювати нулю, оскільки тоді
розв’язок
буде тривіальним. Отже вираз “-![]() ”
буде завжди від’ємним.
З урахуванням нового позначення для
константи маємо два звичайних
диференціальних рівняння першого і
другого порядків:
”
буде завжди від’ємним.
З урахуванням нового позначення для
константи маємо два звичайних
диференціальних рівняння першого і
другого порядків:
![]()
Ці рівняння є однорідними рівняннями стандартного типу з постійними коефіцієнтами. Їх загальні розв’язкі мають вигляд
![]()
де
![]() – довільні сталі.
– довільні сталі.
Підставляючи в добуток X(x)T(t) одержані вирази і об’єднуючи сталі, одержимо функцію виду
![]() ,
(3.5)
,
(3.5)
яка задовольняє рівнянню у частинних похідних. Треба підкреслити, що знайшли нескінченний набір функцій, які задовольняють вихідному рівнянню з частинними похідними.
