
- •3. Елементи релятивістської механіки
- •3.1. Принцип відносності Ейнштейна
- •3.2. Перетворення Лоренця для координат
- •3.3. Перетворення швидкостей у релятивістській механіці
- •3.4. Інтервал між подіями та його інваріантність
- •3.5. Власний час
- •3.6. Власна довжина
- •3.8. Енергія тіла
- •3.8. Зв'язок енергії та імпульсу
- •3.9. Зв'язок маси та енергії спокою
- •3.10. Імпульс та маса фотона
- •3.11. Контрольні питання
3.3. Перетворення швидкостей у релятивістській механіці
Якщо зважити на те, що
компоненти швидкостей тіла в системі
K визначаються як Ux
=
![]() ,Uy
=
,Uy
=
![]() ,Uz
=
,Uz
=
![]() ,
а в системіK'
,
а в системіK'
![]() =
=![]() ,U'y'
=
,U'y'
=![]() ,Uz'
=
,Uz'
=
![]() ,
а диференціалиdx
= (dx'
+ Vdt'),
dt
= (dt'
+ Vdx/c2),
dy
=dy',
dz
= dz'
та dx'
= (dx
- Vdt),
dt'
= (dt
- Vdx'/c2),
то пряма підстановка дає перетворення
швидкостей у вигляді:
,
а диференціалиdx
= (dx'
+ Vdt'),
dt
= (dt'
+ Vdx/c2),
dy
=dy',
dz
= dz'
та dx'
= (dx
- Vdt),
dt'
= (dt
- Vdx'/c2),
то пряма підстановка дає перетворення
швидкостей у вигляді:
|
Uх= |
|
|
Uy
= Uy'·
|
U'y'
= Uy· |
|
Uz
= Uz'·
|
U'z'
= Uz· |
Наприклад, якщо тіло рухається із швидкістю U вздовж осі ОХ, то її перетворення через швидкість U'
у класичній механіці:
U = U' + V,
в релятивістській механіці:
U = (U+V)/(1+VU/c2).
Якщо U' = c, то U = (c+V)/(1+Vc/c2) = c, як того і вимагає постулат Ейнштейна.
3.4. Інтервал між подіями та його інваріантність
Якщо відомі координати двох подій x1, y1, z1, t1 i x2, y2, z2, t1, то величина
s12=![]()
називається інтервалом між цими подіями. Інтервал між двома близькими подіями
ds=![]() ,
де
dl2=dx2+dy2+dz2.
,
де
dl2=dx2+dy2+dz2.
Інтервал s12 між двома подіями однаковий за величиною в усіх інерційних системах відліку (інваріантність s12). Розглянемо це питання докладніше.
Інтервал у рухомій системі відліку К' буде s'2=c2t'122 -l'2, l2=x122+ y122+z122. Проведемо очевидні послідовні перетворення співвідношення c2t12'-x12'2 із врахуванням перетворень Лоренця:
c2t12'-x12'2 = c22(t12 - V x12/c2)2 - 2(x12 - Vt12)2 =
c22(t122 + V2 x122 /c4 - 2 t12 x12V/c2) - 2(x122 + V2t122 - 2 x12Vt12) =
c22(t122+ x122V2 /c4 ) - 2(x122+V2t122 ) = 2[c2t122+ x122V2 /c2- x122 -V2t122]=
 [
t122(c2-V2)-
x122(1-
V2
/c2)]=
c2
t122
- x122.
[
t122(c2-V2)-
x122(1-
V2
/c2)]=
c2
t122
- x122.
Остаточно маємо:
s'2=c2t'122 -l'2 = s2 = c2t122 -l2 = inv.
Часоподібний інтервал. Якщо s122 0, то інтервал s12 називається часоподібним, і для нього існує така система відліку K', в якій дві події відбуваються в одній точці простору x1' = x2', y1' = y2', z1' = z2', а час, що пройшов між ними t12' = s12/c.
Простороподібний інтервал. Якщо s122 <0, то інтервал s12 називається простороподібним, і для нього не існує система відліку K', в якій дві події відбуваються в одній точці простору, але існують системи відліку, в яких вони відбуваються одночасно.
3.5. Власний час
Власний час ' це час, який вимірюється годинником, що рухається разом з системою K'. Проміжок часу між двома подіями в нерухомій системі відліку К за допомогою перетворень Лоренця можна записати через проміжок часу ' у системі K':
'
= ·
 .
.
Дійсно,
якщо подія тривалістю '
= t2'
- t1'
відбувається в системі K'
у точці з координатою х', то тривалість
події у системі K
буде рівна
= t2
- t1
= (t2'
+ Vx'/c2)
- (t1'
+Vx'/c2)
= ',
=
 .
Звідси видно, що'<.
Наприклад, якщо власний час життя
нестабільної елементарної частинки
.
Звідси видно, що'<.
Наприклад, якщо власний час життя
нестабільної елементарної частинки
![]() становить'=10-16
с, то у нерухомій
системі відліку (реєстраційній камері)
час життя буде
= 10-16·/
становить'=10-16
с, то у нерухомій
системі відліку (реєстраційній камері)
час життя буде
= 10-16·/ і приV=0.99c
=
10-16/0.14
= 7.089·10-16c.
При V=0.999c
= 22.37·10-16c.
і приV=0.99c
=
10-16/0.14
= 7.089·10-16c.
При V=0.999c
= 22.37·10-16c.
3.6. Власна довжина
Власна довжина це лінійний розмір L0 тіла в тій системі відліку, де воно знаходиться в стані спокою. Довжина L0 нерухомого тіла, виміряна в системі K' у напрямку її руху відносно системи K із швидкістю V у момент часу t1=t2=t, більша довжини тіла L, що виміряна в системі K.
Дійсно,
L0
= x2'
- x1'
= (x2
- Vt)
- (x1
- Vt)
= (x2
- x1)
= L,
=
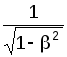 ,
,
L
= L0
 .
.
Звідси видно, що L < L0.
3.7. Основне рівняння релятивістської динаміки
3.7.1. Релятивістська маса
Наведемо без доведення вираз для маси тіла, що залежить від швидкості тіла, так називаної релятивістської маси
![]() .
(1)
.
(1)
У цьому виразі m0- маса спокою, тобто маса нерухомого тіла,- відношення швидкості тілаVдо швидкості світла у вакуумі с.
3.7.2. Релятивістський імпульс
Імпульс визначається як добуток релятивістської маси на швидкість тіла
![]() .
(2)
.
(2)
3.7.3. Основне рівняння динаміки
Основне рівняння динаміки має вигляд такий як і в класичній динаміці, коли воно записується через імпульс
![]() ,
(3)
,
(3)
де
![]() -
релятивістський імпульс (2).
-
релятивістський імпульс (2).
Підставимо в (3) вираз (2) і проведемо диференціювання
![]() ,
,![]() ,
,![]() .
(4)
.
(4)
У (4) поряд з доданком
![]() стоїть доданок, залежний у неявному
вигляді від часу. Цей доданок становиться
рівним 0 тоді коли вектор сили
перпендикулярний швидкості. У цьому
випадку сила є поперечною і під її дією
змінюється лише напрямок швидкості і
стоїть доданок, залежний у неявному
вигляді від часу. Цей доданок становиться
рівним 0 тоді коли вектор сили
перпендикулярний швидкості. У цьому
випадку сила є поперечною і під її дією
змінюється лише напрямок швидкості і![]() .
При цьому вектор прискорення співпадає
за напрямком з вектором сили. Таке
співпадання буде і при паралельності
векторів сили та швидкості.
.
При цьому вектор прискорення співпадає
за напрямком з вектором сили. Таке
співпадання буде і при паралельності
векторів сили та швидкості.




 /(1
- VUx/c2)
/(1
- VUx/c2)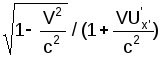
 /(1
- VUxc2)
/(1
- VUxc2)