
- •Глава 1. Транспортная задача: общая постановка, типы и виды моделей 4
- •Глава 2. Методы решения транспортной задачи 13
- •Глава 1. Транспортная задача: общая постановка, типы и виды моделей
- •1.1 Общая постановка, цели, задачи
- •1.2 Основные типы, виды моделей
- •Глава 2. Методы решения транспортной задачи
- •2.1 Диагональный метод, или метод северо-западного угла
- •2.2 Метод минимального элемента
- •2.3 Метод наименьшей стоимости
- •2.4 Метод аппроксимации Фогеля
- •2.5 Метод потенциалов как метод решения транспортной задачи
- •Заключение
- •Список литературы
- •Приложения
Глава 2. Методы решения транспортной задачи
2.1 Диагональный метод, или метод северо-западного угла
При
этом методе на каждом шаге построения
первого опорного плана заполняется
левая верхняя клетка (северо-западный
угол) оставшейся части таблицы. При
таком методе заполнение таблицы
начинается с клетки неизвестного
![]() и заканчивается в клетке неизвестного
и заканчивается в клетке неизвестного![]() ,
т. е. идет как бы по диагонали таблицы
перевозок (приложение 3).
,
т. е. идет как бы по диагонали таблицы
перевозок (приложение 3).
Заполнение
таблицы начинается с ее северо-западного
угла, т. е. клетки с неизвестным
![]() .
Первая база
.
Первая база![]() может полностью удовлетворить потребность
первого заказчика
может полностью удовлетворить потребность
первого заказчика![]()
![]() .
Полагая
.
Полагая![]() ,
вписываем это значение в клетку
,
вписываем это значение в клетку
![]() и исключаем из рассмотрения первый
столбец. На базе
и исключаем из рассмотрения первый
столбец. На базе![]() остается измененный запас
остается измененный запас![]() .
В оставшейся новой таблице с тремя
строками
.
В оставшейся новой таблице с тремя
строками![]() и четырьмя столбцами
и четырьмя столбцами![]() ;
северо-западным углом будет клетка для
неизвестного
;
северо-западным углом будет клетка для
неизвестного![]() .
Первая база с запасом
.
Первая база с запасом![]() может
полностью удовлетворить потребность
второго заказчика
может
полностью удовлетворить потребность
второго заказчика![]()
![]() .
Полагаем
.
Полагаем
![]() ,
вписываем это значение в клетку
,
вписываем это значение в клетку![]() и исключаем из рассмотрения второй
столбец. На базе
и исключаем из рассмотрения второй
столбец. На базе![]() остается новый остаток (запас)
остается новый остаток (запас)![]() .
В оставшейся новой таблице с тремя
строками
.
В оставшейся новой таблице с тремя
строками![]() и тремя столбцами
и тремя столбцами![]() северо-западным углом будет клетка для
неизвестного
северо-западным углом будет клетка для
неизвестного![]() .
Теперь третий заказчик
.
Теперь третий заказчик![]() может принять весь запас с базы
может принять весь запас с базы![]()
![]() .
Полагаем
.
Полагаем![]() ,
вписываем это значение в клетку
,
вписываем это значение в клетку![]() и исключаем из рассмотрения первую
строку. У заказчика из
и исключаем из рассмотрения первую
строку. У заказчика из![]() осталась еще не удовлетворенной
потребность
осталась еще не удовлетворенной
потребность![]() .
.
Теперь
переходим к заполнению клетки для
неизвестного
![]() и т.д.
и т.д.
Через
шесть шагов у нас останется одна база
![]() с запасом груза (остатком от предыдущего
шага)
с запасом груза (остатком от предыдущего
шага)![]() и
один пункт
и
один пункт![]() с потребностью
с потребностью![]() .
Соответственно этому имеется одна
свободная клетка, которую и заполняем,
положив
.
Соответственно этому имеется одна
свободная клетка, которую и заполняем,
положив![]() .
План составлен. Базис образован
неизвестными
.
План составлен. Базис образован
неизвестными![]() .
Правильность составленного плана легко
проверить, подсчитав суммы чисел, стоящих
в заполненных клетках по строкам и
столбцам1.
.
Правильность составленного плана легко
проверить, подсчитав суммы чисел, стоящих
в заполненных клетках по строкам и
столбцам1.
Общий объем перевозок в тонно-километрах для этого плана составит
![]() .
.
2.2 Метод минимального элемента
Суть
метода заключается в том, что из всей
таблицы стоимостей выбирают наименьшую
и в клетку, которая ей соответствует,
помещают меньшее из чисел
![]() и
и![]() .
Затем из рассмотрения исключают либо
строку, соответствующую поставщику,
запасы которого полностью израсходованы,
либо столбец, соответствующий потребителю,
потребности которого полностью
удовлетворены, либо и строку и столбец,
если израсходованы запасы поставщика
и удовлетворены потребности потребителя.
Из оставшейся части таблицы стоимостей
снова выбирают наименьшую стоимость,
и процесс распределения запасов
продолжают, пока все запасы не будут
распределены, а потребности удовлетворены.
.
Затем из рассмотрения исключают либо
строку, соответствующую поставщику,
запасы которого полностью израсходованы,
либо столбец, соответствующий потребителю,
потребности которого полностью
удовлетворены, либо и строку и столбец,
если израсходованы запасы поставщика
и удовлетворены потребности потребителя.
Из оставшейся части таблицы стоимостей
снова выбирают наименьшую стоимость,
и процесс распределения запасов
продолжают, пока все запасы не будут
распределены, а потребности удовлетворены.
Пример
Составить первоначальный опорный план методом минимального элемента для транспортной задачи вида:
|
2 |
3 |
4 |
15 |
|
11 |
6 |
10 |
1 |
|
8 |
9 |
3 |
3 |
|
4 |
1 |
2 |
21 |
|
10 |
20 |
10 |
|
Решение:
Задача сбалансирована.
Строим первоначальный опорный план методом минимального элемента.
Выясним минимальную стоимость перевозок.
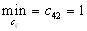 Первая
перевозка будет осуществляться с пункта
производства
Первая
перевозка будет осуществляться с пункта
производства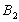 в
пункт потребления
в
пункт потребления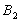 и
она составит максимально возможное
число единиц продукта
и
она составит максимально возможное
число единиц продукта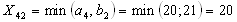 :.
В этом случае, потребности пункта
потребления
:.
В этом случае, потребности пункта
потребления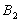 будут
удовлетворены полностью. Значит,
стоимости столбца 2 можно больше не
рассматривать, так как перевозки
будут
удовлетворены полностью. Значит,
стоимости столбца 2 можно больше не
рассматривать, так как перевозки .Выясним
минимальную стоимость перевозок (без
учета столбца № 2).
.Выясним
минимальную стоимость перевозок (без
учета столбца № 2).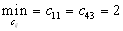 Вторая
и третья перевозки будут осуществляться
с пункта производства
Вторая
и третья перевозки будут осуществляться
с пункта производства
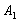 и
и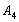 в
пункт потребления
в
пункт потребления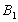 и
и соответственно
и составят максимально возможное число
единиц продукта:
соответственно
и составят максимально возможное число
единиц продукта: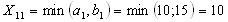 ,
,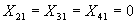 ;
;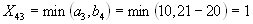
Четвертая перевозка осуществляется с пункта
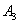 в
пункт потребления
в
пункт потребления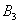 ,
т.к.
,
т.к.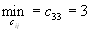 (без
учета первого, второго столбца и
четвертой строки).
(без
учета первого, второго столбца и
четвертой строки).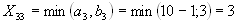 .
.Пятая перевозка осуществляется с пункта
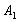 в
пункт потребления
в
пункт потребления ,
т.к.
,
т.к.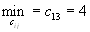 (без
учета первого, второго столбца, третьей
и четвертой строки).
(без
учета первого, второго столбца, третьей
и четвертой строки).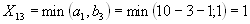 .
.Шестая перевозка осуществляется с пункта
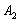 в
пункт потребления
в
пункт потребления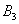 т.к.
т.к.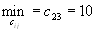 (без
учета первого, второго столбца, первой,
третьей и четвертой строки).
(без
учета первого, второго столбца, первой,
третьей и четвертой строки).
Опорный план имеет вид;
|
10 |
5 |
0 |
|
0 |
1 |
0 |
|
0 |
3 |
0 |
|
0 |
11 |
10 |
