3. Визначення градієнту зміни швидкості.

У чисельній схемі методу молекулярної динаміки використовується друга похідна від координати по часу, тобто прискорення:

,

.

Оскільки моделювання розглядається в наближенні класичної динаміки, то можна використати другий закон Ньютона

.

де – сила, що діє на частинку масою.

Зробимо припущення, що частинки системи - хімічно інертні кульки і сила взаємодії будь-яких двох з них залежить лише від відстані між ними. Тоді ,- потенціал взаємодії двох частинок на відстані. Повна потенціальна енергіясистеми, що міститьчастинок, визначається сумою двочастинкових взаємодій всіх частинок

,

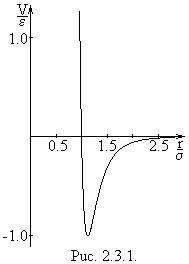
де залежить лише від абсолютної відстаніміж частинкамита. Парна взаємодія такого виду відповідає “простим” рідинам, наприклад рідкому аргону.

Важливими особливостями потенціалу є сильне відштовхування на малих відстаняхі слабке притягання на великих. Наприклад, на атомному рівні відштовхування при малихзумовленеправилом заборони: якщо електронні хмаринки двох атомів перекриваються, деякі електрони повинні збільшувати свою енергію, щоб знаходитися в різних квантових станах - сумарний ефект проявляється у відштовхуванні між електронами, яке називається відштовхуванням кора. Слабке притягання при великих зумовлено взаємною поляризацією атомів - результуюча сила притягання називається силою Ван-дер-Ваальса.

Кожна конкретна модель має свій рецепт визначення градієнта зміни швидкості. Наприклад, для моделі з гармонічним осцилятором враховується сила пружності за законом Гука, для моделі польоту тіла під кутом до горизонту визначаються проекції сил на кожну з осей за законами механіки. У деяких моделях градієнтом може бути не швидкість руху частинки в буквальному сенсі. Наприклад, при моделюванні вистигання тіла це коефіцієнт пропорційності у законі теплопровідності.

При моделюванні системи з багатьох частинок для визначення сили взаємодії між частинками використовують більш формальний підхід і визначають силу, а через неї й прискорення, як похідну енергії по координаті. Серед найбільш вживаних феноменологічних формул – потенціал Ленарда-Джонса та потенціал Борна-Майєра.

4. Визначення сил, що діють на тіло.

При моделюванні системи з багатьох частинок для визначення сили взаємодії між частинками використовують більш формальний підхід і визначають силу, а через неї й прискорення, як похідну енергії по координаті. Серед найбільш вживаних феноменологічних формул – потенціал Ленарда-Джонса та потенціал Борна-Майєра, які враховують вплив системи на кожну частинку через парні взаємодії.

Потенціал Ленарда-Джонса (рис.2.3.1) складається з відштовхувальної та притягальноїчастин

,

- максимальна глибина потенціальної ями при ,

- відстань при .

Даний потенціал є короткодіючим і для практично рівний нулю.

Потенціал Борна-Майєра (рис.2.3.2)

,

відштовхувальний, розширення системи при моделюванні стримується лише граничними умовами.

Потенціал Борна-Майєра часто застосовують для металів (зокрема, міді), експонента описує екранування кулонівської взаємодії електронним газом.

Потенціал Морзе (рис.2.3.3) - потенціал типу Борна-Майєра, який, окрім відштовхування, враховує також притягання

,

- точка рівноваги.

Визначення параметрів модельних потенціалів (Ленарда-Джонса, Борна-Майєра, Морзе та інших) є однією з найскладніших проблем фізики твердого тіла. Вони, як правило, підбираються підгонкою під конкретні, відомі з експерименту, властивості речовини. Проблема полягає в тому, що підгонка під пружні властивості дає можливість добре моделювати пружні властивості, але застосування підібраних параметрів для опису інших властивостей, наприклад, дифузії, дає значно гірші результати. Це пов’язано, зокрема, з тим, що істинна взаємодія в речовині не може бути зведена до суми парних потенціалів. Тому результати, скажімо, молекулярної динаміки з парними потенціалами дають лише якісний опис властивостей твердих тіл. Для кількісного опису зараз розвиваються більш строгі методи (“ab initio” - “з перших принципів”).

Проекцій сил

,