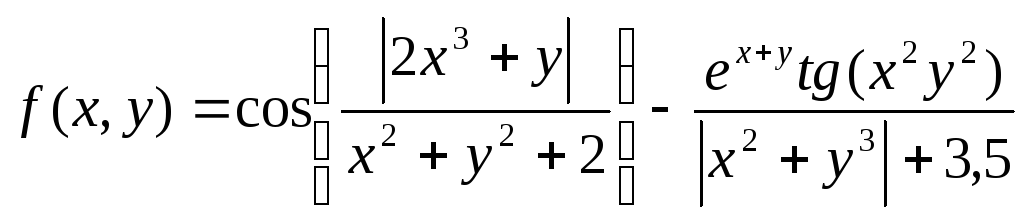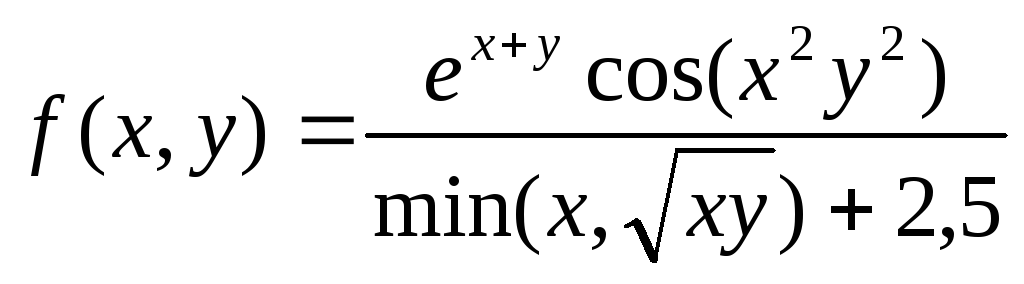Иногда аргументы логических функций становятся громоздкими, если приходится проверять выполнение одного и того же условия элементами блоков ячеек, например:
=ЕСЛИ(И(А4>=B2;B4>=B2;C4>=B2;D4>=B2;E4>=B2;F4>=B2); “Да”; “Нет”)
Условие можно записать короче, если в аргументе функции использовать блок ячеек:
=ЕСЛИ(И(А4:F4>=B2); “Да”; “Нет”)
Задания по лабораторной работе
Задание № 1
Задание 1.1 Форматирование данных.
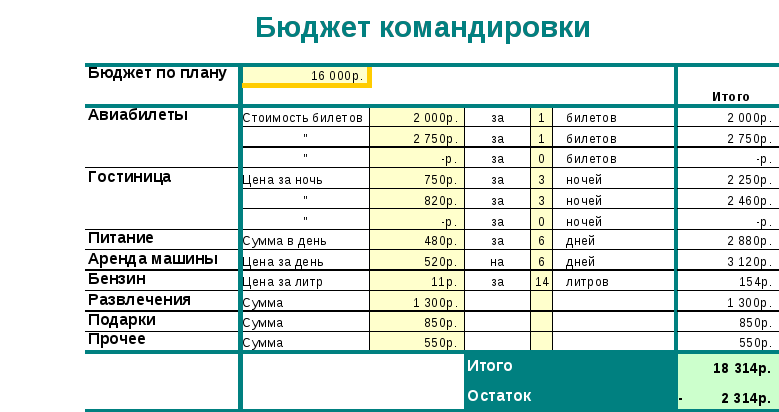
Используя основные приемы форматирования создать на листе 1 (название листа 'Бюджет командировки', цвет ярлыка - розовый) таблицу “Бюджет командировки”, на основе представленного на рисунке образца.
Задание 1.2. Условное форматирование и создание таблицы значений функции двух переменных. Построение графика поверхности.
Используя смешанные ссылки, построить на листе 2 (название листа 'Функция f(x,y)', цвет ярлыка - синий) рабочей книге таблицу значений функции двух переменных f(x,y) в виде:
|
|
x1 |
… |
xm |
|
y1 |
f(x1, y1) |
… |
f(x1, ym) |
|
… |
… |
… |
… |
|
yn |
f(xn, y1) |
… |
f(xn, ym) |
Функцию двух переменных, границы и шаг изменения аргументов взять из таблицы № 1. Диапазоны изменения аргументов x и y совпадают. С помощью функций MS Excel определить: максимальное, среднее, минимальное среди найденных табличных значений функции. C помощью средства «Условное форматирование» среди табличных значений функции красным цветом выделить значения превышающее среднее значение и синим – значения, ниже среднего. На этом же листе текущей рабочей книги построить график поверхности f(x,y).
Пример выполнения задания:
Построить
таблицу квадратов двухзначных чисел,
по принципу
,
гдеx
и y
принимают значения от 1 до 9. (см. рис. 1.)
Рисунок 1. Таблица квадратов двухзначных чисел
Для этого:
В столбце A и строке 5 ввели числа от 1 до 9 и выдели эти области желтым цветом;
В ячейку B6, используя смешанныессылки ввели функцию:=($A6*10+B$5)^2 и используя средства автозаполнения получили все значения функции f(x,y)
Замечание: При использовании смешанных ссылок необходимо учитывать:
абсолютная ссылка по столбцу – фиксирует только столбец (при копировании изменяется только строка, столбец не изменяется, если копирование происходит в пределах одной строки (в разные столбцы), то адрес ячейки не изменится);
абсолютная ссылка по строке – фиксирует только строку (при копировании изменяется только столбец, строка не изменяется, если копирование происходит в пределах одного столбца (в разные строки), то адрес ячейки не изменится).
Применяя функции: MAКС(), МИН(), СРЗНАЧ() для полученных табличных значений находим максимальное, среднее, минимальное среди найденных значений функции;
С помощью команды Формат - Условное форматированиезадаем условия и требуемые форматы (см. рисунок 2).
Рисунок 2. Окно ”Условное форматирование”
Для построения графика поверхности выполняются шаги:
Выделить найденный диапазон табличных значений;
Вызов мастера диаграмм;
Выбор типа диаграммы:Поверхность;
Просмотр отображаемого результата, и размещение легенды снизу;
Для изменения количества цветовых градаций на графике поверхности необходимо вызвать контекстно-зависимое меню для легенды “Формат легенды” и во вкладкеШкалапоменять цену основных делений так, чтобы градаций стало5;
Остальные параметры диаграммы установить, как показано на примере.
Таблица № 1 Индивидуальные задания
|
№ |
Функция f(x,y) |
Диапазон изменения аргументов функции |
Шаг изменения аргументов hx, hy |
|
1 |
|
[1, 6] |
0.2 |
|
2 |
|
[1, 5] |
0.25 |
|
3 |
|
[0, π/2] |
π/20 |
|
4 |
|
[0, π] |
π/10 |
|
5 |
|
[0, π/2] |
π/20 |
|
6 |
|
[π/2, 3π/2] |
π/12 |
|
7 |
|
[0, π] |
π/10 |
|
8 |
|
[1,2] |
0.1 |
|
9 |
|
[-π, π] |
π/10 |
|
10 |
|
[-5,5] |
0.25 |
|
11 |
|
[-5, 5] |
0.5 |
|
12 |
|
[0,1] |
0.1 |
|
13 |
|
[0,1] |
0.1 |
|
14 |
|
[-π, π] |
π/8 |
|
15 |
|
[-1,1] |
0.25 |
