4 Энергия и мощность сигнала

Если к резистору с сопротивлением R приложено постоянное напряжение U, то выделяющаяся в резисторе мощность будет равна:

За время Т в этом резисторе выделяется тепловая энергия:

Пусть теперь к тому же резистору приложено не постоянное напряжение, а сигнал S(t). Рассеивающаяся в резисторе мощность при этом тоже будет зависеть от времени (речь идет о мгновенной мощности).

Чтобы вычислить теряющуюся за время T энергию, мгновенную мощность необходимо проинтегрировать:

Можно ввести и понятие средней мощности за заданный промежуток времени, разделив энергию на длительность временного интервала:

Во все приведенные формулы входит сопротивление нагрузки R. Если энергия и мощность интересуют нас не как физические величины, а как средние сравнения различных сигналов, этот параметр можно из формул исключить (принять R=1). Тогда мы получим определение энергии мгновенной мощности и средней мощности, принятой в теории сигналов

- энергия сигнала

- мгновенная мощность

(1)

Данные параметры иногда называются удельной мощностью и энергией, чтобы подчеркнуть, подразумевая при этом единичное значение сопротивления нагрузки.

Энергия сигнала может быть конечной или бесконечной. Любой сигнал конечной длительности будет иметь конечную энергию, а любой периодический – бесконечную. Если энергия сигнала бесконечна, можно определить его среднюю мощность на всей временной оси. Для этого из формулы (1) путем предельного перехода, устремив интервал усреднения в бесконечность

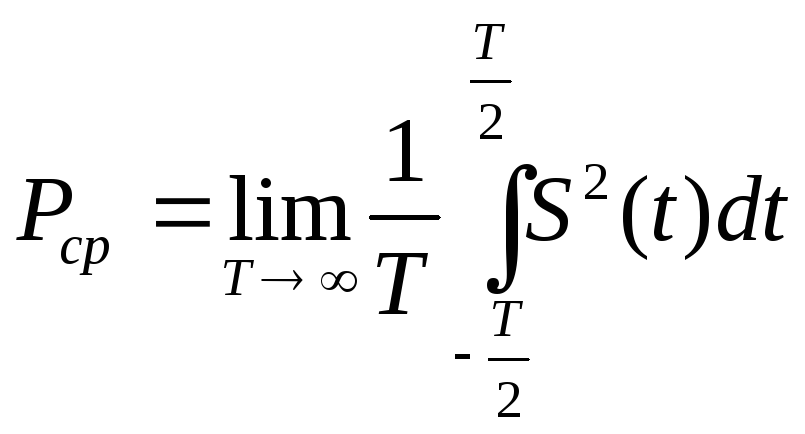(2)

Квадратный корень из Рср даст среднеквадратичное значение мощности сигнала

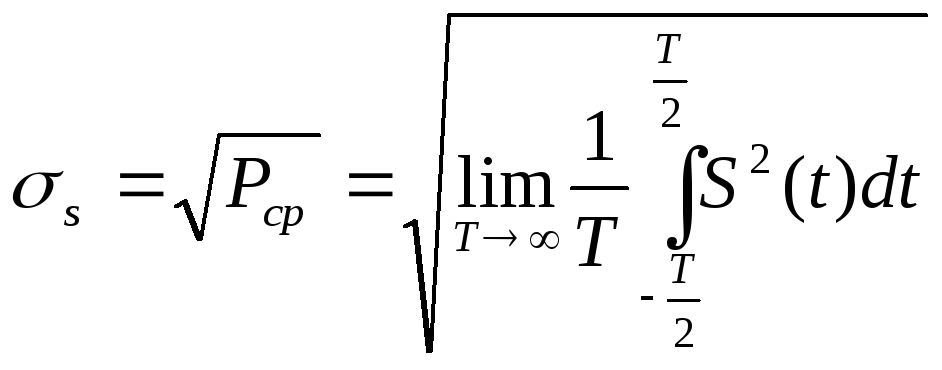(3)

5 Спектральный анализ периодических сигналов. Условия Дирихле. Ряд Фурье.

Для периодического сигнала с периодом Т выполняется соотношение:S(t+nT) = S(t) при любом t.

где n - произвольное целое число; Т – период сигнала.Величина обратная периоду называется частотой повторения сигнала (f = 1/T). Используют понятие круговой частоты. (ω = 2πf)

Разложению в ряд Фурье могут подвергаться периодические сигналы.

Чтобы такое разложение существовало, фрагмент сигнала длительностью в один период должен удовлетворять условиям Дирихле:

1. не должно быть разрывов 2-го рода (с уходящими в бесконечность ветвями функции)

2. число разрывов 1-го рода (скачков) должно быть конечным

3. число экстремумов должно быть конечным

Различают несколько форм записи ряда Фурье:

1. синусно – косинусная

2. вещественная

3. комплексная

Синусно-косинусная форма записи ряда Фурье

Входящие в формулу кратные основной частоте (ω₁) частоты называются гармониками. Гармоники нумеруются в соответствии с индексом k, частота ω _k = k ω ₁ называется к-ой гармоникой сигнала.

Коэф-ты, входящие в данный ряд определяются след образом:

; ;

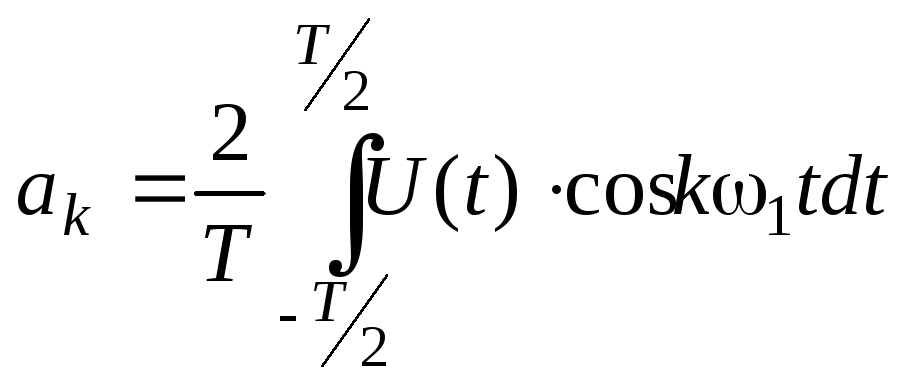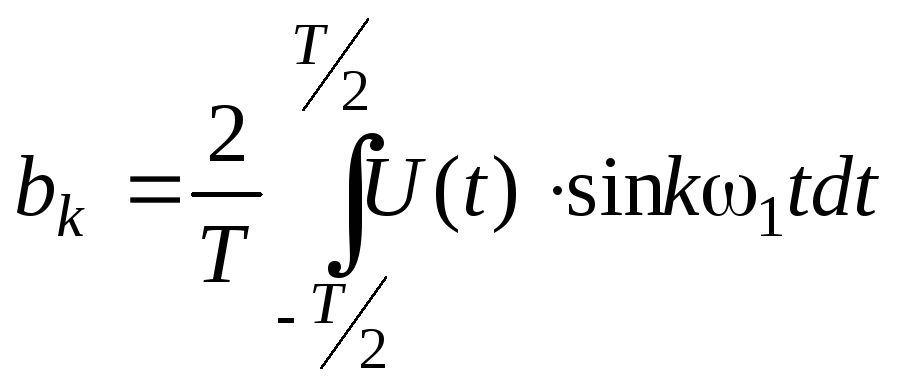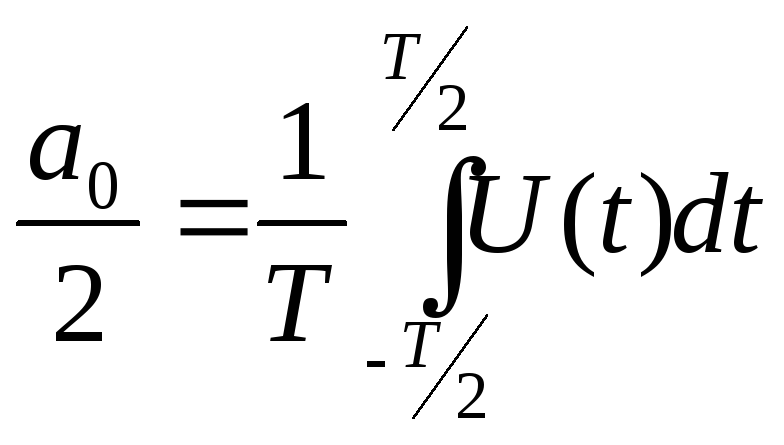
a₀/2 – среднее значение с-ла на периоде.

Если S(t) - чётная ф-ция, то все b_к = 0 и в ф-ле ряда Фурье будут только косинусные слагаемые. Если S(t) - нечётная ф-ция, то все а_к = 0 и в ф-ле ряда Фурье будут только синусные слагаемые.

Вещественная форма записи

Некоторое неудобство синусно-косинусной формы ряда Фурье состоит в том, что для каждого значения индекса суммирования к в формуле фигурируют два слагаемых синус и косинус.

, где ;- фазаk-ой гармоники.

Если S(t) является чётной функцией фазы φ_к могут принимать значения 0 и π, а если S(t) функция нечётная, то возможны значения фазы ±π/2.

Комплексная форма записи

Данная форма представления является наиболее употребимой в радиотехнике. Она получается из вещественной формы представления косинуса в виде полусуммы комплексных экспонент. Вытекает из формулы Эйлера: е^jx = cos(x) + jsin(x), cos(x) = ½ ( e^jx + e^-jx ).

Применив данное преобразование к вещественной форме ряда Фурье получим:

.

Учитывая, что ,получим 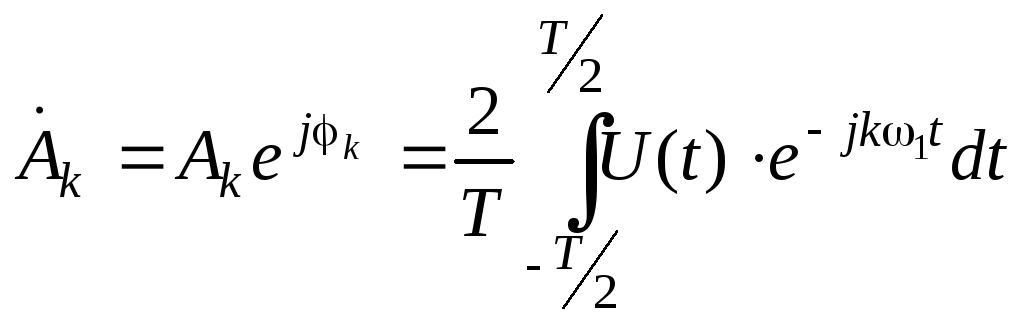. Формулы называются парой преобразований Фурье. Вторая формула из них позволяет найти спектр, т.е. совокупность гармонических составляющих, образующих в сумме колебание.

Спектр периодической последовательности импульсов состоит из постоянной составляющей и множества гармонических составляющих, частоты которых образуют дискретный ряд значений () кратных основной частоте колебаний. Амплитуды гармонических составляющих или сокращенно гармоник равны, а начальные фазы. Такой спектр называется дискретным или линейчатым. Постоянную составляющую можно рассматривать как гармонику с нулевой частотой колебания и амплитудой_.