Вопрос 8.4 Замена системы пружин эквивалентной пружиной

При описании колебательного движения систему пружин, действующих на материальную точку, заменяют одной пружиной, жесткость которой равна жесткости системы. Эту пружину называют эквивалентной. Рассмотрим три основные схемы соединения пружин.

1 Параллельное соединение(рисунок 8.1).

П

Рисунок 8.1

араллельно соединенные пружины, если их деформации одинаковы, можно заменить эквивалентной пружиной, коэффициент жесткости которой равен сумме коэффициентов жесткости соединенных пружин,

.

2 Последовательное соединение(рисунок 8.2).

При последовательном соединении нескольких пружин они могут быть заменены эквивалентной пружиной, податливость которой равна сумме податливостей соединенных пружин (податливостью пружины называют величину, обратную коэффициенту жесткости). Следовательно, коэффициент жесткости эквивалентной пружины в данном случае определяется следующим образом:

.

3

Рисунок 8.2

«Двухстороннее» соединение(рисунок 8.3).

П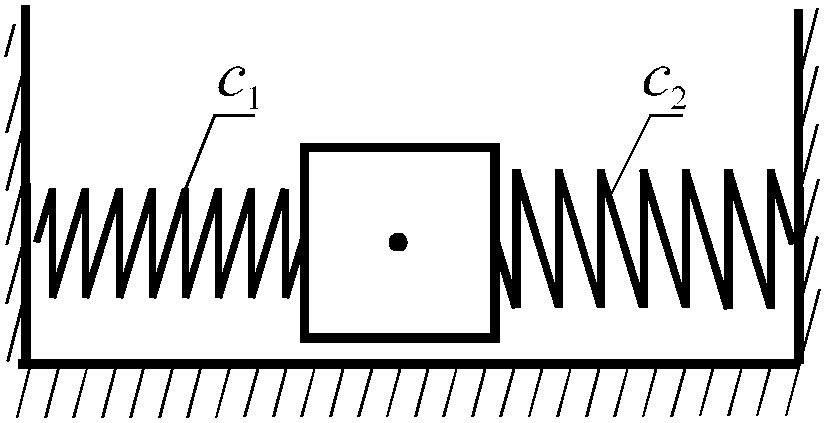ри движении исследуемой материальной точки деформации обоих пружин будут одинаковы. Результирующая сила, действующая со стороны этих пружин на точку, будет равна сумме сил упругости в пружинах 1 и 2. Следовательно, коэффициент жесткости эквивалентной пружины будет равен сумме коэффициентов жесткости пружин 1 и 2:

.

Любую систему пружин можно представить как набор рассмотренных схем.

Рисунок 8.3

Лекция 9 Динамика материальной системы.

(2 часа, 1 семестр, 2 курс)

Вопрос 9.1Теорема о движении центра масс материальной системы.

Центром масс материальной системы называют точку, радиус-вектор которой определяется по формуле

,

где – масса материальной системы;

m_i,– масса и радиус-векторi-й материальной точки.

Координаты центра масс системы:

,

где x_i,y_i,z_i– координаты центра массi-го тела системы.

При решении задач динамики материальной системы часто оказывается полезной теорема о движении центра масс:произведение массы материальной системы на ускорение ее центра массa_C равно геометрической сумме внешних сил, приложенных к системе:

.

В ходе решения выражение теоремы проецируют на оси координат. При этом получается система уравнений

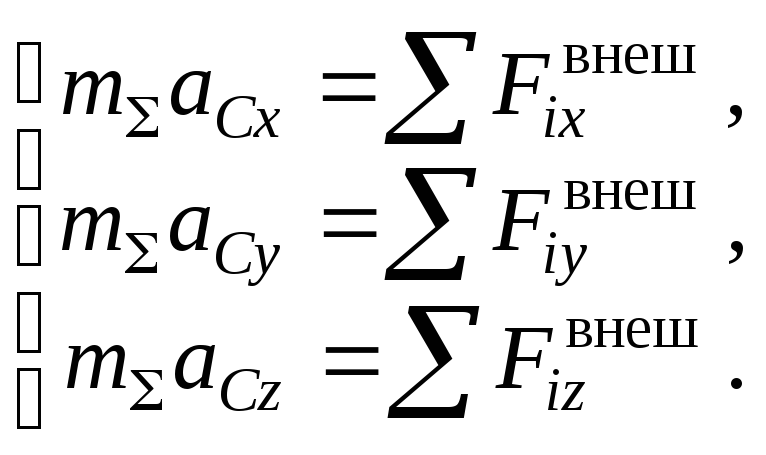
Использование теоремы о движении центра масс материальной системы для решения задач динамики рекомендуется осуществлять по следующей методике:

1 Изображается материальная система, и указываются все внешние силы, действующие на нее.

2 Выбираются оси координат.

3 Внешние силы, действующие на систему, проецируются на выбранные оси.

4 Записываются выражения координат центра масс системы через координаты центров масс одного из тел системы.

5 Дифференцируя выражения координат центра масс по времени, получают зависимости для скорости и ускорения центра масс системы.

6 Полученные выражения подставляются в систему динамических уравнений.

7 Решается дифференциальное уравнение относительно искомой координаты с учетом заданных начальных условий.

Вопрос 9.2Динамические уравнения движения твердого тела.

Динамические уравнения движения твердого тела устанавливают связь между кинематическими характеристиками движения тела и действующими на него силами.

Поступательное движение тела.В этом случае динамическое уравнение представляет собой следствие из теоремы о движении центра масс:

,

где m– масса тела;

– ускорение центра масс тела;

–i-тая сила, действующая на тело.

При решении задач динамическое уравнение поступательного движения тела проецируют на оси координат.

Вращательное движение тела. Для него динамическое уравнение имеет вид:

,

где J_z– момент инерции тела относительно оси вращенияz;

 – угловое ускорение тела;

M_iz– моментi-й силы относительно оси вращения.

При составлении динамического уравнения вращательного движения тела выбирается направление отсчета угла поворота . Моменты сил, вращающих тело против выбранного направления, принимаются отрицательными, а по выбранному направлению – положительными.

Момент инерции J_z является мерой инертности тела при вращательном движении. Момент инерции материальной системы относительно данной осиOzопределяется как сумма произведений масс всех точек системы на квадраты их расстояний от этой оси:

.

Для абсолютно твердого тела суммирование по точкам системы заменяется интегрированием по объему

,

где ρ – плотность материала тела;

h– расстояние от точки с координатамиx,y,zдо осиOz.

Момент инерции J_Cтела относительно осиCz, проходящей через центр массC, называютцентральным моментом инерции. Если для тела известенрадиус инерцииi, то центральный момент

.

Центральные моменты инерции некоторых тел:

1 Тонкий однородный стержень с массой mи длинойl:

.

2 Тонкое круглое однородное кольцо с массой mи радиусомR:

.

3 Круглый однородный диск с массой mи радиусомR:

.