Экзаменационный билет № 9
1. Установите отношение между логическими формами:
ØA «B и ØВ Ú А
Решение: Составим таблицу
-
A
B
ØA
ØA «B
ØB
ØВ Ú А
1
0
0
1
1
0
1
1
0
0
0
1
0
0
1
0
1
1
0
1
1
1
0
0
Значения логических форм не совпадают, поэтому логические формы находятся в отношении противоречия.
Проверьте правильность следующего силлогизма:
«Некоторые деятели искусства талантливы. Значит, некоторые писатели талантливы, ибо все писатели - деятели искусства»
Решение:
Схема рассуждения следующая
Некоторые деятели искусства (М -) талантливы(Р)
Все писатели (S) - деятели искусства (М—)
__________________________________________
Некоторые писатели талантливы
Нарушено правило средний термин должен быть распределен хотя бы в одной из посылок.
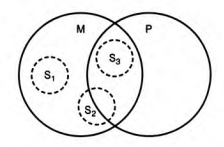
Средний термин (М) не распределен в большей посылке, так как является субъектом частного суждения, и не распределен в меньшей посылке как предикат утвердительного суждения. Следовательно, средний термин не распределен ни в одной из посылок, поэтому необходимую связь между крайними терминами (S и Р) установить нельзя, что видно из схемы, на которой изображены три возможных случая:
1) «Ни один писатель не является талантливым» (S1);
2) «Некоторые писатели талантливы» (S2);
3) «Все писатели талантливы» (S3).
Экзаменационный билет № 10
Верно ли, что:
Из pÚq следует p?
Из p«q следует p?
Из p следует pÚq?
Решение:
(pÚq) ® p
Если p «ложь», q «истина», то (pÚq) будет «истинно».
Если (pÚq) «истинно» и р «ложь», то (pÚq) ® p «ложно».
Ответ: неверно.
(p«q) ® p
Если p «ложь», q «ложь», то (p«q) будет «истинно».
Если (p«q) «истинно» и р «ложь», то (p«q) ® p «ложно».
Ответ: неверно.
p®(pÚq)
Если p «ложь», то p®(pÚq) будет «истинно».
Если p «истина», то (pÚq) будет «истинно». А значит и p®(pÚq) будет «истинно».
Ответ: верно.
Можно ли восстановить без нарушения правил следующую энтимему:
«Он – лакей, следовательно, не человек»
Решение:
Схема силлогизма следующая
Он – лакей.
Все лакеи не являются людьми
Он – не человек
Экзаменационный билет № 11
Проанализируйте вывод, который имеет следующую логическую форму, используя сокращенный (нетабличный ) метод проверки:
((A ® B) Ù (ØBÚС))® (ØС ® ØA) .
Правилен ли он?
Решение:
Наша схема – импликация. Она принимает значение «ложно» лишь однажды – когда посылка (A ® B) Ù (ØBÚС) принимает значение «истинно», а заключение (ØС ® ØA) – значение «ложно».
Поскольку схема (ØС ® ØA) (согласно п.1) принимает значение «ложно», значит ØС «истина», ØA – «ложно». Получим, что С – «ложно», А – «истина».
Поскольку ((A ® B) Ù (ØBÚС) есть конъюнкция, и она истинна, постольку каждый член этой конъюнкции, по определению, истинен, т.е. A®B, (ØBÚС) истинны.
Так как (ØBÚС) – истинная дизъюнкция (согласно п.3) и С – «ложно» (согласно п.2), то ØB должно быть истинным. Значит, сами В ложными.
Поскольку A®B – истинная импликация (согласно п. 3) и B ложно (согласно п.4), то и A тоже ложно.
Итак, получилось, что А одновременно принимает и значение «ложно» (согласно п.5), и значение «истинно» (согласно п.2). Но это невозможно, ибо А может принять лишь одно из двух значений. Данное противоречие – результат допущения в пункте 1, от которого придется отказаться и признать, что наша схема – логический закон.
Ответ: правилен
Соблюдены ли основные правила силлогизма в следующем случае:
«Все склонные к горячности люди неразумны.
Некоторые ораторы не склоны к горячности.
Следовательно, некоторые ораторы разумны»
Решение:
Схема рассуждения следующая
Некоторые ораторы не склоны к горячности
Все склонные к горячности люди не являются разумными
__________________________
Некоторые ораторы разумны
Не соблюдается 1-е правило посылок: хотя бы одна из посылок должна быть утвердительным суждением.
Ответ: нет