Основные свойства определенного интеграла

Свойство 1.	Величина определенного интеграла не зависит от обозначения переменной интегрирования: .
Свойство 2.	Определенный интеграл с одинаковыми пределами интегрирования равен нулю: .

Свойство 3.

При перестановке пределов интегрирования определенный интеграл меняет знак: .

Свойство 4.

Постоянный множитель можно выносить за знак определенного интеграла: .

Свойство 5.

Если на отрезке взять точку, то .

Свойство 6.

Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме определенных интегралов:

Свойство 7.

Определенный интеграл в симметричных относительно нуля пределах от четной функции равен удвоенному интегралу на половине интервала интегрирования: , если - четная.

Например:

.

.

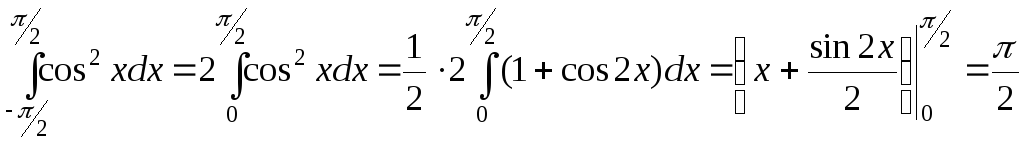Свойство 8.

Определенный интеграл в симметричных пределах от нечетной функции равен нулю: , если – нечетная.

Например:

; .

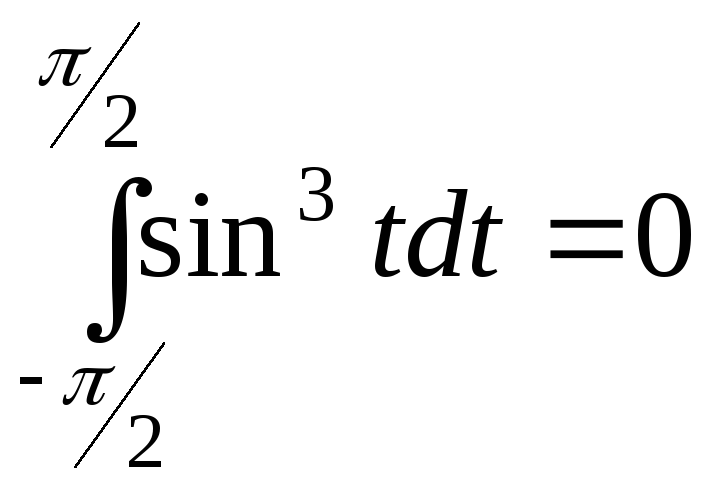Примеры вычисления определенных интегралов.

1. ;

2. 

;

3. ;

4. .

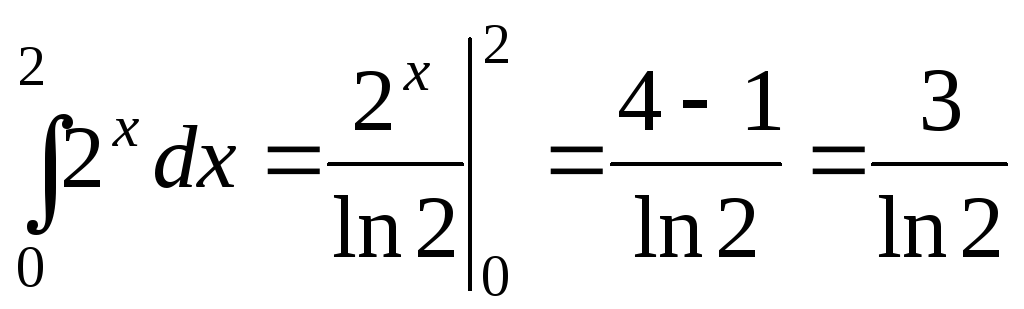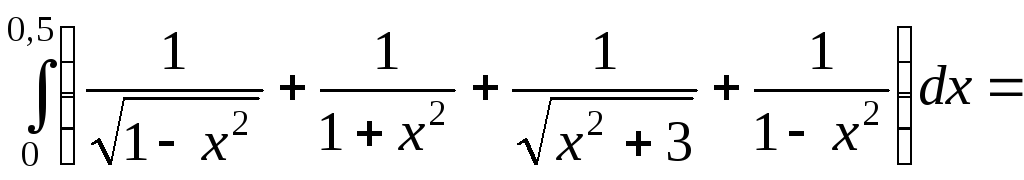
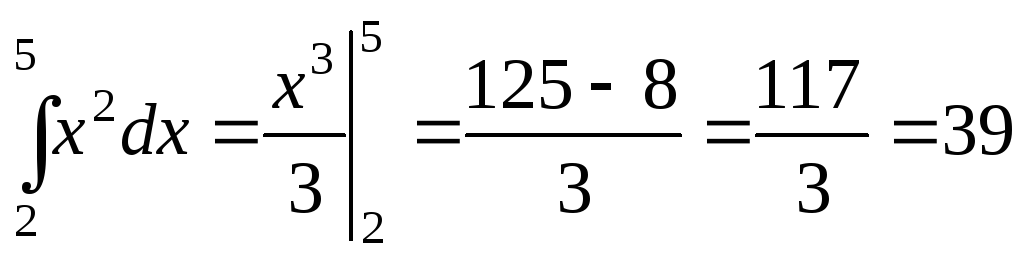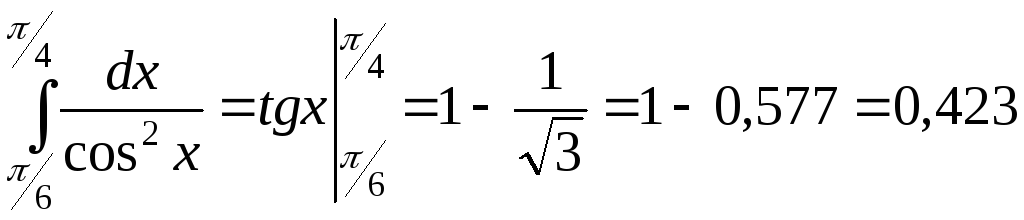II. М е т о д ы и н т е г р и р о в а н и я

Все методы интегрирования предназначены для преобразования заданного интеграла к одному или нескольким табличным значениям. Эта главная идея реализуется многими способами.

2.1. Метод непосредственного интегрирования

Непосредственное интегрирование состоит в том, что подынтегральное выражение тождественными преобразованиями представляется в другой форме, - такой, чтобы после применения к ней свойств неопределенного или определенного интеграла получить табличное выражение. Известны различные подходы к преобразованию подынтегрального выражения:

1. –	подынтегральное выражение представляют в виде дифференциала некоторой функции.
2. –	используют линейное изменение аргумента.
Применяют алгебраические преобразования и упрощения, используют известные формулы, тождества и соотношения.

Ранее уже приводились примеры на использование этих подходов. Возьмем еще несколько примеров:

а)

.

Здесь перешли от произведения функций к их сумме, затем воспользовались свойством для суммы интегралов.

б)

.

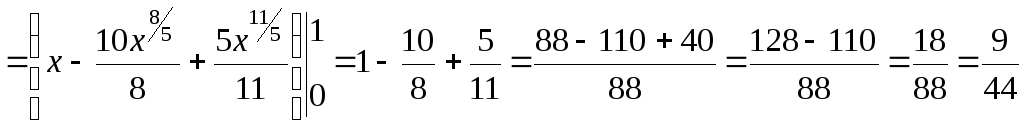В данном примере возвели функцию в квадрат и использовали свойства интегралов.

в) .

В этом примере основное тригонометрическое тождество позволило перейти к табличным интегралам.

г)

.

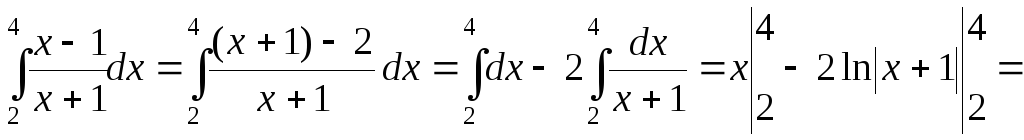
В числителе дроби выделили выражение, совпадающее со знаменателем, в результате чего получили табличные интегралы.

д) .

В этом примере использовали известные соотношения для тригонометрических функций, с целью преобразования заданного интеграла к табличному.

2.2. Метод замены переменной

Теорема 3.

Если справедливо равенство и переменнуюзаменить по формуле, гдеимеет непрерывную производную, то справедливо равенство: .

Если в интеграле от переменной перейти к переменной, то получим новый интеграл с преобразованным подынтегральным выражением. Замена оправдана и целесообразна, если вновь полученный интеграл проще заданного, т.е. он быстрее приводится к табличному.

Правило 1.

При замене переменной в неопределенном интеграле после вычислений необходимо возвратиться к старой переменной .

Правило 2.

В определенном интеграле при замене переменной необходимо найти новые пределы интегрирования, а возвращение к старой переменной не проводится.

Правило подстановки. Чтобы вычислить интеграл:

необходимо выполнить следующие действия:

а) переписать интеграл в виде:

;

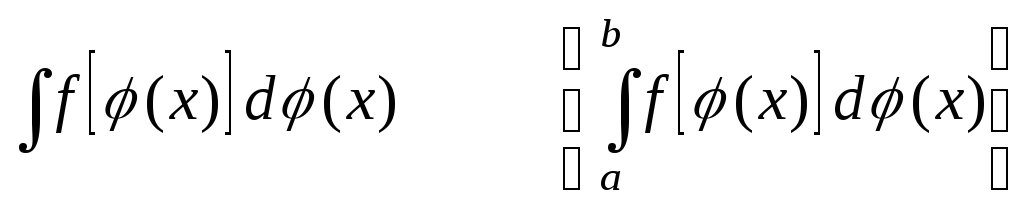б) заменить новой буквой, например, и получить:

;

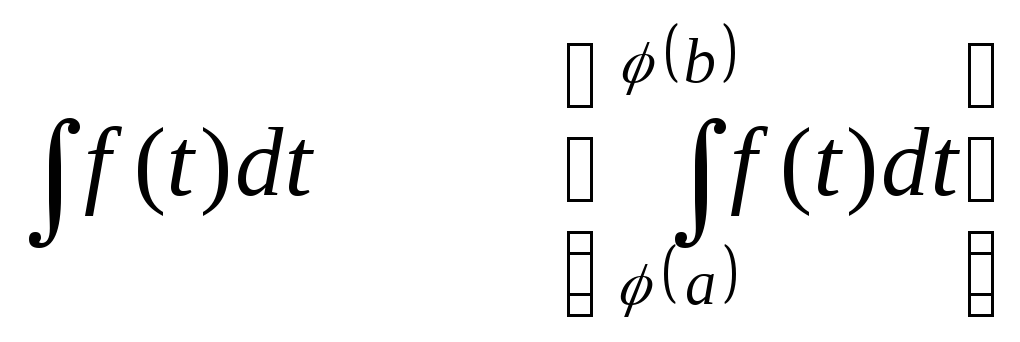в) вычислить вновь полученный интеграл.

Например.

а)

;

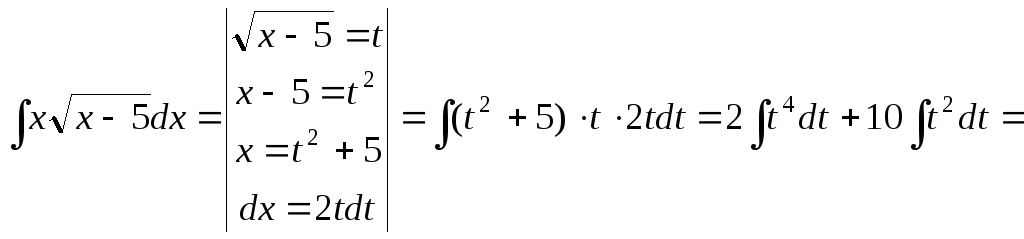
б) ;

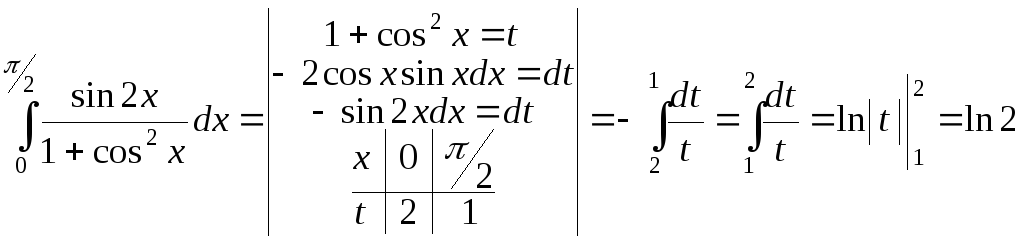в) ;

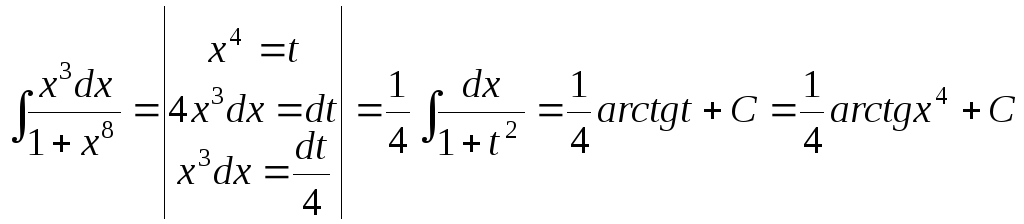г) ;

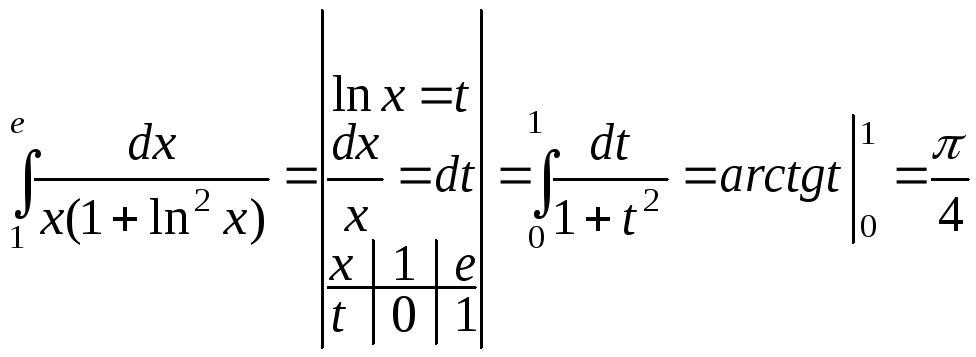д) ;

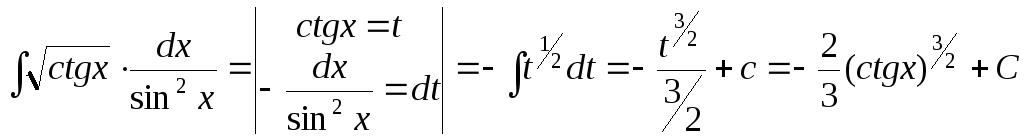е) .

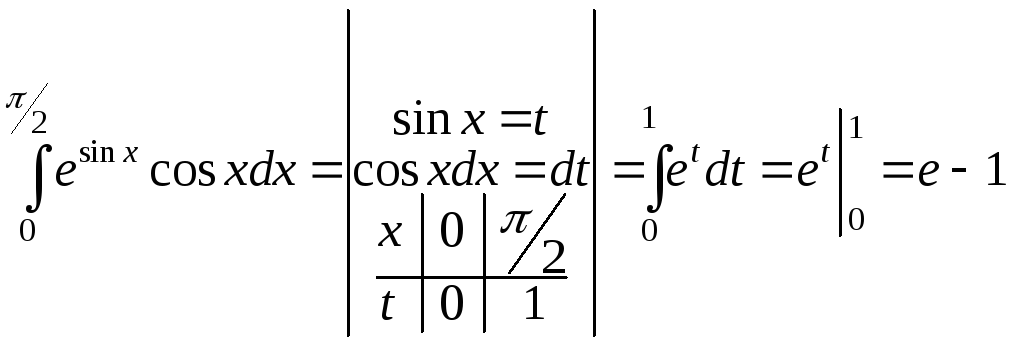Замечание. Если в числителе дроби находится производная знаменателя, то интеграл равен модулю логарифма.

Например:

а) ;

б) .