
Конспект лекций по ТМРГ / Конспект лекций по ТМРГ
.pdf
41
Застосуємо теорему імпульсів класичної механіки до ділянки рідини поміж перерізами
1-1 і 2-2.
Проекція на повільно визначену вісь (вісь трубопроводу) прирощення кількості руху дорівнює сумі імпульсів зовнішних сил, що діють на ділянку, що розглядається, за певний час (нехай час Т=1с):
∑mVx = ∑(Pτ)x
Із зовніших сил в рівняння включаємо тільки силу гідродинамічного тиску Р, тому що силу тертя на малої ділянці не враховуємо.
∑P - сума сил в напрямку руху потоку – сума сил тиску. m =αρQ
αρQ(V2 −V1 )= ∑P
αρQ =αρω2V2
αρω2V2 (V2 −V2 )= (P1 − P2 )ω2
Поділимо це останнє рівняння на γω2 та приймемо α=1
P1 − P2 |
= |
|
(V22 −V1V2 )αρ |
* |
|||
|
γ |
|
|
g |
|||
|
|
|
|
|
|||
P |
− P |
= |
V 2 |
−V V |
|
||
1 |
2 |
|
2 |
1 2 |
|
|
|
|
γ |
|
|
g |
|
||
|
|
|
|
|
|||
Складемо рівняння Бернулі для перерізів 1-1 і 2-2 та підставимо з рівняння його части- ну P1 −γ P2
|
P |
|
V 2 |
|
|
|
|
|
P |
|
|
V |
2 |
|
+ h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
+ |
|
|
|
1 |
|
|
= |
|
2 |
+ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
γ |
|
|
2g |
|
|
|
|
|
γ |
|
|
|
2g |
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
hm |
= |
|
|
P |
− P |
+ |
V 2 |
−V 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
γ |
|
|
|
|
|
|
|
|
2g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
h |
= |
|
V 2 |
|
|
−V V |
+ |
V |
2 |
|
−V |
2 |
= |
2V 2 |
− 2V V |
|
+V 2 |
−V |
2 |
= |
(V |
−V |
2 |
)2 |
||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
1 2 |
|
|
|
|
1 |
|
2 |
1 |
|
|
1 2 |
|
|
1 |
|
2 |
1 |
|
|
||||||||||||||||||||
|
|
m |
|
|
|
|
|
|
|
2g |
|
|
|
|
|
|
|
|
|
|
|
|
2g |
|
|
|
|
|
|
2g |
|
|
|
|
|
|
|
|
2g |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
V1 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
hm |
|
|
|
V2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V2 |
|
ω2 |
|
|
|
V1 |
|
|
ω1 |
|
|
|
|
|
|
|
||||||||||||
= |
|
|
|
|
|
|
|
|
− |
|
|
|
|
= |
|
|
|
|
|
−1 |
|
= |
|
|
− |
|
|
|
|
|
|
|
||||||||||||||||
|
|
2g |
|
|
|
|
|
1 |
|
|
|
2g |
|
|
2g |
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
V2 |
|
|
|
|
|
|
|
|
|
|
|
|
ω1 |
|
|
|
|
|
|
ω2 |
|
|
|
|
|
|
|
|||||||||||||||
ξ |
|
= |
|
ω |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
2 |
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
ω1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ξ |
|
= |
|
|
|
|
ω |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
1− |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
ω2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

42
Втрати напору в діфузорах (трубках, що повільно розширюються). Діфузор характеризується кутом розкриття чи конусністю.
Рис. 28. Втрати напору на повільному розширенні потоку (діфузорі)
hдиф = hp. р. k
|
ω |
|
2 |
|
|
2 |
|
ξдиф = k |
ω1 |
−1 |
|
|
|
||
Тут hдиф - втрати напору у діфузорі
ξдиф - коефіціент гідравлічного опору
hр-р - втрати напору на раптовому розширенні k - коефіціент пом’якшення.
Втрати напору в діфузорі будуть меньші, ніж при раптовому розширенні потоку, оскільки віхорові зони повільно згладжуються.
Втрати напору в діфузорі визначаються як для раптового розширення, але з помноженням на коефіціент зм’якшення к<1, який залежить від куту конусності α.
Значення кофіціентів наведені в довіднику Кисильова. αопт = 20 − 25o - оптимальне зниження α.
Рис. 29. Область оптимального значення коефіциєнта зм’якшення К
Втрати напору при раптовому звуженні потоку.

43
Рис. 30. Визначення втрат напору на „раптовому звуженні” потоку.
Частинки рідини, які входять в вузький переріз намагаются зберегти свою траекторію за інерцією та формують так званий стиснений переріз ω c.
Втрати напору, взагалі, виникають при розширенні перерізу від ω c. до ω 2.
|
|
|
ω |
|
|
|
2 |
|
1 |
|
2 |
||
|
|
2 |
|
|
|
|
|||||||
ξрз |
|
|
|
|
|
|
|
|
|||||
= |
ωc |
−1 |
|
= |
ε |
−1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
h |
|
=ξ |
V |
2 |
=ξ |
V |
2 |
|
|
||||
|
|
|
|
2 |
|
|
2 |
|
|
||||
рз |
2 2g |
рз 2g |
|
|
|||||||||
|
|
|
|
|
|
||||||||
Тут ξ - ступінь стиснення струмини, чи коефіціент стиснення.
ε= ωc
ω2
ωc. - стиснений переріз вимірити дуже складно, тому в розрахунках використовують
емпірічні значення ε по таблицях, наприклад, в довіднику Кисильова [4]. При ω 1>>ω 2 ε =0.611 (стечіння з резервуару) ξ =0.42
Втрати напору в повільно звуживаючихся трубах (конфузорах).
Рис. 31.Втрати напору на повільному звуженні потоку (конфузорі)
Втрати напору визначаються також, як для раптового звуження, але з помноженням на кофіціент пом’якшення, який є меньш за одиницю. У відповідності до куту конусності α1 <1 в
довідниках подається графічна або таблична залежність.

44
Рис. 32. Область оптимального значення коефіциєнта зм’якшення К1
ξп.з. = K1 1 −1 2
ε
Значення ξп.з. для конфузорів наведені в довіднику Кисильова [4] в залежності від співвідношення більшого та меньшого перерізів.
Втрати напору у відводах, колінах, кутниках.
Коліни утворюють тим більші гідравлічні опори, чим більш різький їх поворот, тобто чим меньший їх радіус заоколення R. Коліно вдається гострим, якщо r=R. Для такого коліна
ξк =1. Взагалі для більш повільних колін та відводів в довіднику Кисильова [4] наведені значення ξк .
|
|
|
|
|
|
|
|
|
|
|
Рис. 33. Втрати напору у коліна, відводах, трикутниках. |
||
ξK = |
|
1 |
|
2 |
|
|
|
|
−1 |
, де ε в залежності від співвідношення R/d. |
|||
ε |
||||||
Втрати напору в діафрагмах.

45
Діафрагма – штучне утворене раптове звуження потоку в трубопроводах. Вона існує для гасіння напору, або для виміру витрати (вимірювальна діафрагма). В останьому випадку ураховується зв’язок втрат напору з величиною швидкості та витрати в трубопроводі.
Рис. 34. Втрати напору в діафрагмах.
|
|
ω |
2 |
|
ω |
e |
ξd = |
|
|
|
|
|
|
|
|
ω0 |
||||
ω0ε |
−1 |
, де ε = |
||||
Значення ξd та ε подані в таблицях довідника Кисильова [4].
Втрати напору в трійниках.
Існують дві групи трійників – нагнетаючі та всмоктуючі, або припливні (1) та втяжні (2).
Рис. 35. Схеми до визначення коефіциентів місцевих опорів для трикутников або хрестовин.
В трійниках відрізняють магістраль та відгалуження.
Поворіт потоку може відбуватися на кут ≥90°.
Втрати напору залежать від схеми роботи трійника в потоці, від куту між магістральними напрямком та відгалудженням α, від співвідношення їх діаметрів ξ та hm
залежать, до якої швидкості їх віднести: до магістралі чи до відгалудження, до чи після відгалудження. Всі можливі схеми наведені в довіднику Кисильова [4].
Втрати напору в заслінках і вентилях.
Втрати напору в заслінках і вентилях виникають в результаті зменьшення перерізу трубопроводу. Взагалі, як для раптового звуження потоку.

46
Рис. 36. Втрати напору в заслінках та вентилях.
Значення ε подані в довіднику Кисильова, в залежності від ступення відкриття заслінки або вентилю. Але повністю відкрита арматура утворює опір своїм клапаном. Для повністю відкритої заслінки рекомендується брати ε =0.1, а для повністю відкритого вентеля ξв =5 [4].
Втрати напору на зварних стиках.
Втрати напору на зварних стиках визначаються по експереминтальним залежностям. Досліди показали, що вплив стиків можна розглядати як збільшення коефіціента гідравлічного тертя λ.
Рис. 37. Вплив стиків труб на збільшення гідравлічного тертя.
λ′ = λ +ξст dl
ξcm - індивідуальний опір стику (по довіднику Кисильова від засобу зварювання).
λ- коефіціент Дарсі без стиків.
λ’- те ж зі стиками.
Залежність коефіціентів місцевих опорів від числа Рейнольдса.

47
Рис. 38. Визначення коефіциентів гідравлічних опорів в не квадратичній області гідравлічного опору.
Для великих чисел Рейнольдса, відповідних квадратичнії зоні гідравлічного опору, залежність ξ =f(Rе) зникає. При малих числах Rе – залежить значно. Довідні значення ξ обчислені для квадратичної області опору. Для переходу в другі області є формула:
ξ= ReA +ξкв , де
А– довідна величина, яка дається в залежності від значення Rе.
Взаємний вплив місцевих опорів.
При гідравлічному розрахунку втрати напору можна складати по всім розташованим
там місцевим опорам тоді, коли вони знаходяться на відстані одного від одного, більш ніж відстань впливу.
ξзаг = ∑ξi i=1n
Відстань впливу – це відстань, на якій епюра швидкостей, деформована попереднім місцевим опором, відновлює форму. Відстань впливу визначається з співвідношення:
dl = 0,5 ξλ
dl - калібр труби. Для інженерних розрахунків припускається dl =20÷30.
В іншому випадку опори сумуються також, але додається коефіціент запасу, який ураховує зниження точності розрахунків.

48
ЛЕКЦІЯ 8.
Витікання рідини з отворів та насадків.
1. Витікання рідини з малого отвору в тонкій стінці, при сталому напорі.
Отвір визначається малим, якщо його розмір по висоті значно меньший, ніж напір – не більш ніж 0,1Н.
Тонка стінка – це стінка з гострою крімкою. Рідина, що витікає з такого отвору долає тільки місцеві перешкоди.
Рис. 39. Схема витікання рідини з малого отвору в тонкій стінці при сталому напорі.
При витіканні струмина на деякому відстані випробує стиск перерізу від ω до ωс .
ε = ωωc - коефіціент стиснення.
Стиснення буває повне, коли просліджується по всьму периметру, та неповне, коли отвір примикає до будь-якої перешкоди. В тім місці струмина не має бокового стиснення. Наприклад, отвір примикає до стінки або до дна судини.
Стиск буває досконалим, коли отвір знаходиться на значному відстані від стінок та до дна судини, та вони не виказують впливу на нього деформацією струмини, що витікає. Та досконалим, коли виказує певний вплив.
m>3а – доскональне стиснення, де a – розмір отвору
m – відстань від стінок до дна.
Складемо рівняння Бернулі відносно площини n-n, що проходить крізь центр ваги отвору в тонкій стінці для перерізів 1-1 і C-C:
49
H + |
αV 2 |
P |
|
P |
αV 2 |
+ h |
|
0 + |
aт |
= |
ат |
+ |
|
||
|
|
|
|||||
|
2g |
γ |
|
γ |
2g |
вт |
|
|
|
|
|||||
Тут hвт - втрати напору на вхід в отвір.
hвт =ξвх V 2
2g
V ≈ 0 (переріз резервуару надто великий)
H = (1+ ξвх )V2g2
|
V = |
1 |
2gH , |
Q =ωV |
|
1 |
+ξвх |
|
|
1 |
=φ -коефіціент швидкості |
|
||
1+ξвх |
|
|||
|
V =φ |
2gH |
(1) |
|
|
Q = μω |
2gH |
(2) |
|
μ= φε = ωωc φ - коефіціент витрати отвору.
Удовіднику Кисильова подані значення ϕ та μ і ξ в залежності від форми отвору та схеми роботи отвору (затоплений чи ні).
Швидкість витікання з отвору в тонкій стінці
V = φ 2gH
Витрати витікання з отвору в тонкій стінці
Q = μω 2gH
2. Витікання з отвору в тонкій стінці при змінному напорі.
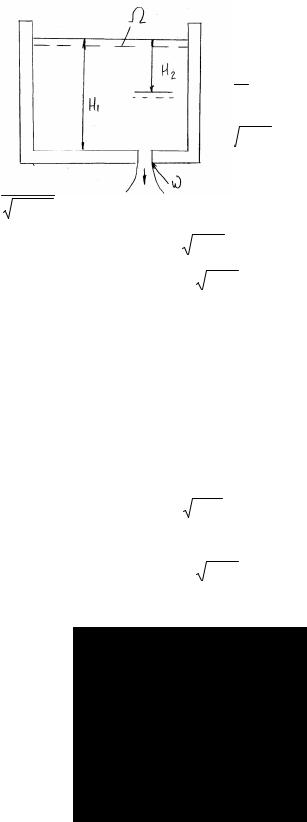
Рис. 40. |
Витікання |
тонкій стінці при змінному напорі. |
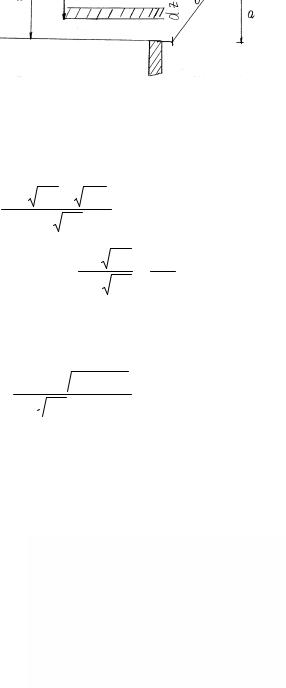
50
Тут Ω - площа вільної поверхні резервуару.
Ураховуючи, що напір в процесі витікання змінюється над отвіром від Н1 до Н, вираз для швидкості витікання з такого отвору та витрата будуть аналогічні виразам (1) і (2), але зі значенням середньої величини напору Нсер:
V =φ |
2gHсер |
|
Q = μω 2gHсер |
||
Hсер = |
H1 + H 2 |
|
2 |
|
|
|
|
|
Ці вирази придатні до приблизних розрахунків. |
||
Час випорожнення резервуару при витіканні напору над отвором від Н1 до Н2.
t = |
2Ω( H1 − H 2 ) |
|
|
|
||||
|
μω |
|
2g |
|
|
|
||
При Н2=0 t |
0 |
= |
2Ω H1 |
= |
2W |
, де W - об’єм резервуару. |
||
μω 2g |
Q |
|||||||
|
|
|
|
|
||||
Є два резервуари з глибинами Н1 та Н2 і вільними поверхнями Ω1 і Ω2 , які з’єднані тонкою стінкою з отвіром площиною ω , тоді час зрівняння їх рівнів:
t = 2Ω1Ω2  H1 − H 2 зр μω
H1 − H 2 зр μω  2g (Ω1 + Ω2 )
2g (Ω1 + Ω2 )
3. Витікання з великого отвору в тонкій стінці при сталому напорі.
Отвір вважається великим, якщо його висота а>0,1Н. Тут
Рис. 41. Витікання рідини з великого отвору при постійному напорі.
z – відстань елементарної смужки від поверхні рідини; b – ширина смужки перерік, або ширина отвору;
а – висота отвору;
