
Конспект_инжинерная графика
.pdf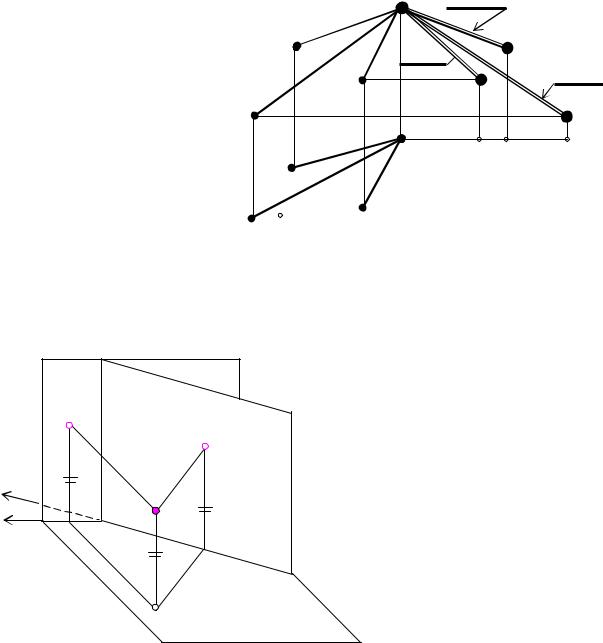
|
|
|
|
|
|
|
|
|
|
31 |
Якщо необхідно визначити натуральні величини відрізків, що виходять з однієї точки, |
||||||||||
зручно скористатися способом обертання навколо осі, перпендикулярної до площини |
||||||||||
проекцій. Цей спосіб теоретично нічим не відрізняється від ППП, траекторія руху, при |
||||||||||
цьому, буде коло. |
|
|
|
|
|
|
|
|
|
|
Задача. Визначити натуральні величини відрізків SA, SB, SC. |
|
|
|
|
|
|||||
Розв’язання |
задачі |
|
S2 |
н. в. SA |
|
|
|
|||
зрозуміло з рисунку (рис. 6). |
|
|
|
|
||||||
Спосіб обертання |
|
A2 |
н.в.SB |
|
A21 |
|
|
|||
|
|
|
|
|
|
|
||||
застосовується |
при |
побудові |
|
|
|
|
н.в. SC |
|||
|
|
B21 |
|
|
|
|||||
розгорток пірамід. |
|
C2 |
B2 |
|
|
|
|
C21 |
||
|
|
|
S1 |
|
|
|
|
|||
|
|
|
|
|
A11 |
|
|
C11 |
||
|
|
|
A1 |
|
B11 |
|
|
|||
|
|
|
S1A1 = S1A11; S1B1 = S1B11; |
|||||||
|
|
|
|
|||||||
|
|
|
C1 |
B1 |
S1C1 = S1C11. |
|
||||
|
|
|
|
|
|
|
|
Рис. 6 |
||
|
|
|
|
|
|
|
|
|
||
2.4. СПОСІБ ЗАМІНИ ПЛОЩИН ПРОЕКЦІЙ. РОЗВ’ЯЗАННЯ ОСНОВНИХ ЗАДАЧ |
|
|||||||||
СПОСОБОМ ЗПП |
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗПП |
Сутність способу заміни площин |
||||||
П2 |
|
|
проекцій полягає в тому, що |
|||||||
|
|
|
||||||||
А2 |
|
|
|
геометричний |
|
об'єкт |
залишається |
|||
|
А4 |
П4 |
незмінним, а |
|
площини |
проекцій |
||||
|
|
|
||||||||
|
|
послідовно |
замінюються |
доти, |
||||||
|
|
|
|
|||||||
|
|
А |
|
поки ми не прийдемо до одного з |
||||||
х14 |
|
|
чотирьох можливих відповідей, до |
|||||||
х12 |
|
|
|
одного |
з зображень |
на |
площині |
|||
|
|
|
проекцій, де й одержимо відповідь |
|||||||
|
|
|
|
|||||||
|
|
|
|
простим виміром на кресленні. |
||||||
|
|
|
|
На |
рис.7 |
|
показана |
|
схема |
|
|
|
А1 |
П1 |
одержання |
нової |
фронтальної |
||||
Рис. 7 |
|
проекції точки А на площині |
||||||||
|
|
|
проекцій П4, що розташована |
|||||||
|
|
|
|
перпендикулярно до |
горизонталь- |
|||||
ної площини проекцій П1. Зберігається ортогональний напрямок проекціювання. |
|
|
|
|||||||
На кресленні нова проекція точки А знаходиться на лінії проекційного зв'язку, що |
||||||||||
перпендикулярна нової осі і відстань від нової проекції точки до нової осі дорівнює відстані |
||||||||||
від замінної проекції точки до старої осі. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
32 |
А2 |
|
В2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
П2 |
|
|
|
|
|
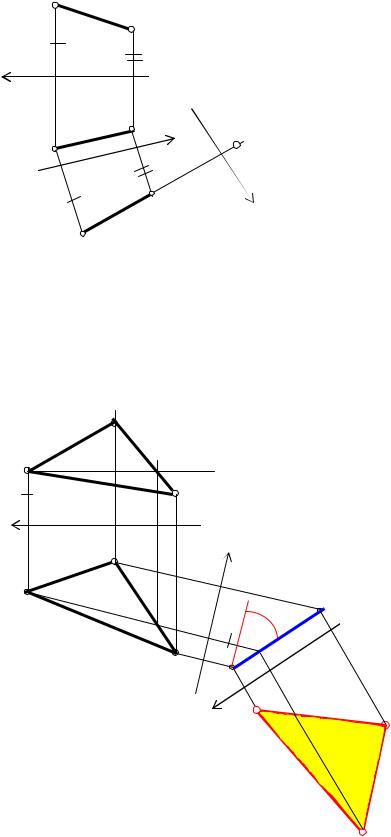
На рис. 8 приведено розв’язання |
||||||
X12 |
|
|
|
|
задачі ЛТ, тобто одержання нової |
|||||||
|
|
В1 |
П1 |
|
проекції відрізка прямої у вигляді точки. |
|||||||
А |
|
А5 В5 |
Розв’язання задачі потребувало двох |
|||||||||
|
|
|
П4 |
|
послідовних замін. |
|
|
|
|
|
|
|
|
|
|
|
П5 |
|
|
|
|
|
|
|
|
|
|
|
В4 |
П4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А4 |
|
Рис. 8 |
|
|
|
|
|
|
|
|
|
На рис.9 |
приведено розв’язання задачі ПН, тобто визначення натуральної величини |
|||||||||||
|
|
В2 |
|
|
|
|
плоскої фігури. |
Для |
||||
|
|
|
|
|
|
цього |
було |
виконано |
||||
А2 |
|
|
|
|
|
|
дві |
заміни |
площин |
|||
|
|
|
|
|
|
проекцій. |
|
Спочатку |
||||
|
|
|
|
|
|
|
|
|||||
П2 |
|
|
C2 |
|
|
|
площина |
П2 |
була |
|||
|
|
|
|
|
замінена на площину |
|||||||
|
|
|
|
|
|
|||||||
X12 |
|
|
|
X14 |
|
|
П4 |
|
(при |
цьому |
||
П1 |
|
В1 |
П1 |
|
|
одночасно визначився |
||||||
|
|
|
П4 |
|
|
кут |
|
нахилу |
|
|||
|
|
|
|
В4 |
П4 |
|
||||||
А1 |
|
|
|
|
площини |
трикутника |
||||||
|
|
|
|
|
АВС |
|
до |
|
горизон- |
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
C1 |
А4 |
|
П5 |
тальної |
|
площини |
|||
|
|
|
|
|
|
проекцій), |
|
а |
потім |
|||
|
|
|
C4 |
|
|
площина |
П1 |
була |
||||
|
|
|
X45 |
C5 |
|
В5 |
замінена на площину |
|||||
|
|
|
|
П5. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Н.в |
|
|
|
|
|
|
|
|
|
Рис. 9 |
|
|
А5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
2.5. ОБЕРТАННЯ НАВКОЛО ЛІНІЇ РІВНЯ. СУМІЩЕННЯ |
|
|
|
|
|
|||||||||
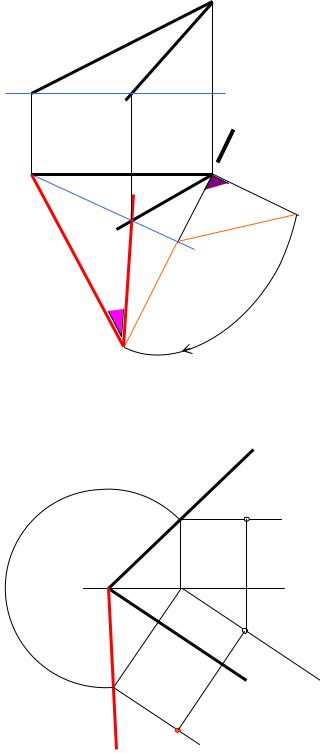
Обертання навколо ліній рівня застосовується для розв’язання планіметричних задач. |
||||||||||||||
|
|
|
|
|
|
Сутність цього способу |
полягає в тому, |
що |
||||||
|
|
|
|
S2 |
при |
обертанні |
точки |
навколо |
осі, |
|||||
|
|
|
|
|
|
перпендикулярної до площини проекцій, |
||||||||
|
|
|
|
|
|
площина обертання точки перпендикулярна до |
||||||||
А2 |
|
В2 |
|
|
осі обертання. Це дозволяє визначити центр і |
|||||||||
|
h2 |
|
||||||||||||
|
|
радіус обертання. |
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
Розглянемо конкретний приклад. |
|
|
|||||||
|
|
|
|
S1 |
|
|
Визначити |
натуральну |
величину |
кута |
||||
А1 |
|
|
|
|
між прямими a і b обертанням навколо |
|||||||||
|
|
|
|
|
горизонталі. |
|
|
|
|
|
|
|
||
|
В1 |
|
|
|
Розв’язання. Проводимо |
горизонталь |
h, |
|||||||
|
h1 |
|
|
|
||||||||||
|
|
відмічаємо точки А и В на осі обертання. |
||||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
Через точку |
S |
проводимо |
площину |
, |
||||
|
|
|
|
|
|
перпендикулярну |
осі |
обертання |
h. |
|
На |
|||
|
|
|
|
|
кресленні |
(рис.10) |
цьому |
відповідає |
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
проведення через S1 сліду-проекції |
1 |
|||||||
|
S0 |
|
|
|
Рис.10 |
горизонтально-проекціюючої |
площини |
. |
||||||
|
|
|
|
|
Відмічаємо точку О – центр обертання |
|||||||||
(О h |
|
|
|
|
|
|||||||||
) |
і |
визначаємо |
натуральну |
величину радіуса обертання ОS способом |
||||||||||
прямокутного трикутника. Відмітимо, що пряма SА в нашому випадку паралельна |
||||||||||||||
фронтальній площині проекцій і на кресленні S0А1 |
дорівнює S2А2. |
|
|
|
|
|
||||||||
|
|
|
|
f20 |
|
|
Ця |
обставина |
використовується |
в |
||||
|
|
|
|
|
способі суміщення – це є обертання навколо |
|||||||||
|
|
|
|
|
|
|||||||||
|
|
|
F2 |
h2 |
А2 |
сліду. На рис.11 показане суміщення точки |
||||||||
|
|
|
|
|
А |
з горизонтальною площиною проекцій |
||||||||
|
|
|
|
|
|
обертанням навколо горизонтального сліду |
||||||||
х12 |
X |
|
F1 |
f10 |
h20 |
h0. Відрізок фронтального сліду XF2 |
||||||||
|
|
|
|
|
відкладений в натуральну величину XF на |
|||||||||
|
|
|
|
|
А1 |
площині проекцій П1 таким чином, що точка |
||||||||
|
|
|
|
|
F попадає на траєкторію переміщення точки |
|||||||||
|
|
|
|
|
h1 |
|||||||||
|
F |
|
|
|
F при обертанні навколо сліду h0. |
|
|
|
||||||
|
|
h |
|
h10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
А0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
f0 |
Рис. 11 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
34
2.5. Матеріали для підготовки до контрольної роботи № 1 |
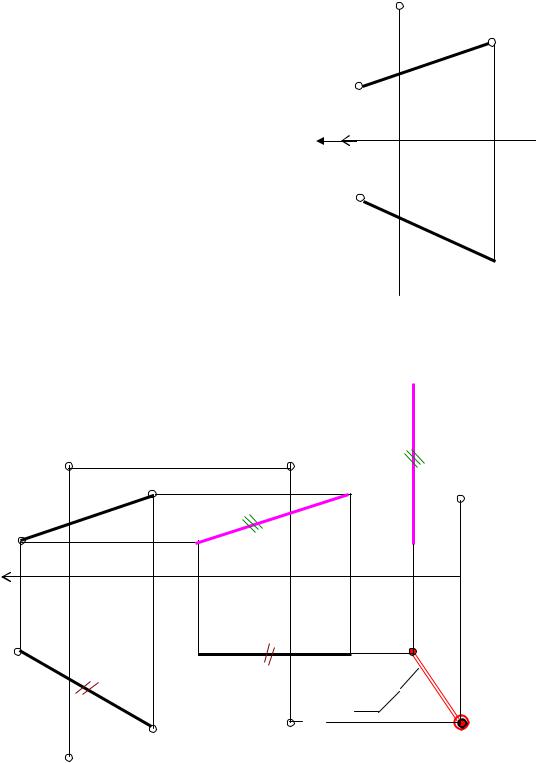
Задача № 4 |
||||||
Плоскопараллельним |
переміщенням |
визначити |
|
|
|
А2 |
|
натуральну величину відстані від точки А до |
|
|
|
||||
прямої ВР. |
|
|
|
|
|
|
С2 |
Пряму ВC |
і точку А переміщаємо паралельно П1 |
|
В2 |
||||
|
|
||||||
так, щоб пряма |
ВC |
розташувалася |
паралельно до |
|
|
||
фронтальної площини проекцій П2 – на кресленні цьому |
|
|
|
|
|||
|
|
|
|
||||
відповідає розташування В1 С1 / /х12 , а фронтальні проекції |
|
П2 |
|
||||
точок переміщаються по прямих, паралельним осі х12 , |
|
|
|||||
одержимо В2 С2 - натуральна величина ВC. |
|
х12 |
|
|
|
||
|
|
|
|||||
Друге плоскопараллельне переміщення здійснюємо |
|
|
|
|
|||
|
П1 |
|
|||||
паралельно П2 - на кресленні цьому відповідає вертикальне |
|
|
|||||
розташування В2 С2 |
і тому що горизонтальні проекції |
|
|
|
|
||
точок переміщаються по прямим паралельним осі х12 , те |
|
В1 |
|
||||
пряма ВC спроецирується в точку. |
|
|
|
||||
 С1
С1
 А1
А1
|
|
|
|
|
|
|
|
|
В2 |
|
А2 |
~ |
|
|
|
А2 |
|
|
|
|
C2 |
~ |
|
|
|
С2 |
|
А2 |
|
В2 |
~ |
|
|
|
В2 |
|
|
||
|
|
|
|
С2 |
х12 |
|
|
|
|
|
~ |
~ |
|
|
|
В |
В1 |
С1 |
|
В1 |
1 |
С1 |
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
А1 |
|
|
|
А~1 |
|
|
|
С1 |
|
|
|
|
|
|
|
|
|
А1 |
|
|
|
Для завершення задачі необхідно виділити на прямій ВР точку,
~
найближчу до точки А. Для цього з точки A2 проводимо перпендикуляр
~ ~
до прямої B2 C2 , отриману точку переносимо на вихідні проекції.
|
|
|
|
|
|
|
А2 |
|
35 |
|
Задача № 5 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
В2 |
|
С2 |
|
|
|
|
|
|
|
|
|
|
Способом |
заміни |
площин |
проекцій |
|
П2 |
|
|
||
|
|
|
|
||||||
|
|
|
|
|
|||||
визначити: |
|
|
|
|
|
х12 |
|
|
|
Відстань від точки А до прямій ВC. |
|
|
|
|
|
||||
|
|
П1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В1 |
|
|
|
|
|
|
|
|
|
|
С1 |
|
|
|
|
|
|
|
|
А1 |
|
|
|
|
|
|
|
|
|
|
|
|
Способом |
заміни |
площин |
проекцій |
|
В4 |
|
|
П1 |
|
|
|
|
П4 |
х14 |
|||||
визначити: |
|
|
|
|
|
|
|
||
Натуральну величину ( АВС). |
|
|
|
|
|
|
|||
|
|
С2 |
|
|
|
А4 |
C4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А5 |
В5 С5 |
|
|
|
|
|
|
|
|
d |
||
А2 |
|
h2 |
|
|
|
П4 |
|
|
|
|
|
|
|
|
П5 |
|
|
||
|
|
|
|
|
|
|
|
|
|
П2 |
|
|
|
|
|
х14 |
х45 |
|
|
|
|
В2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|||
х12 |
|
|
|
П1 |
П4 |
|
|
|
|
П1 |
|
|
|
|
|
|
|||
|
С1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
С4 |
|
|
||
|
|
|
|
|
|
|
|||
А1 |
|
|
|
|
|
|
|
||
|
h1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
А4 |
|
|
|
|
|
|
|
|
|
h4 |
|
|
|
|
|
|
В1 |
|
В4 |
|
|
|
|
|
|
|
П4 |
|
|
|
С5 |
|
|
|
|
|
х45 |
П5 |
В5 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Н.в. АВС |
|
|
|
|||
А5
36
РОЗДІЛ 3. БАГАТОГРАННИКИ ТА КРИВІ ПОВЕРХНІ.
У перетині граного тіла площиною, в загальному випадку одержимо багатокутник.
3.1. ПЕРЕТИН ГРАННИХ ТІЛ ПЛОЩИНОЮ. Багатокутник перетину можна одержати двома способами:
1.Визначити його вершини, що з'єднуються в деякій послідовності, і таким чином, одержати сторони цього багатокутника.
2.Визначити прямі, на яких знаходяться сторони його. Потім, на отриманих прямих визначити вершини шуканого багатокутника перетину, з'єднуючи які, оформити креслення з урахуванням видимості його сторін.
Упершому випадку, використовується перша основна позиційна задача курсу нарисної
геометрії для визначення вершин багатокутника перетину – спосіб ребер.
В другому випадку, використовується друга основна позиційна задача курсу нарисної геометрії для визначення прямих багатостороника перетину способом граней.
Спосіб ребер може застосовуватися для будь-яких граней багатогранника, спосіб граней – тільки для його граней перпендикулярних площинам проекцій. Отже, спосіб граней раціонально застосовувати для прямих призм. Розглянемо приклади використання цих способів для побудови трикутника перетину MNK.
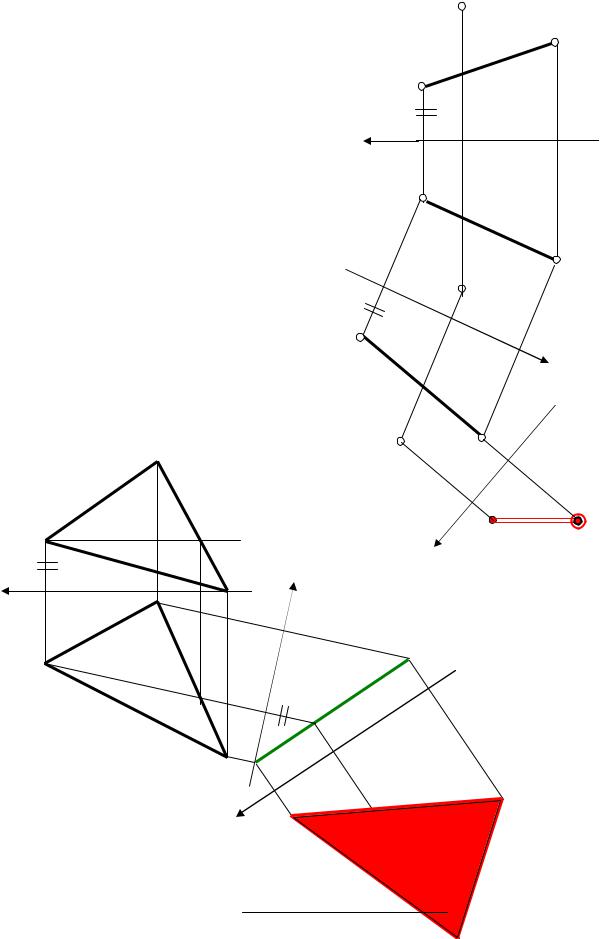
|
|
СПОСІБ РЕБЕР: Побудувати трикутник MNK перетинання похилої піраміди SABC із |
||||||||
|
|
площиною (m n). |
|
|
|
|
|
|
|
|
|
|
Розв’язання задачі способом ребер виконується в такій послідовності (Рис. 1): |
|
|||||||
Задача. Побудувати перетин трикутної |
Задача. Побудувати перетин прямої |
|
||||||||
наклоної піраміди площиною (m n). |
трикутної призми площиною (m n). |
|
||||||||
|
|
|
|
|
|
S2 |
A2 |
B2 |
C2 |
|
|
|
|
|
1 |
|
|
|
|
m2 |
|
|
|
m |
|
3 |
5 |
|
|
2 |
|
|
|
|
|
|
|
N2 |
|
||||
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
M2 |
|
|
|
|
|
|
|
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N2 |
|
|
n2 |
|
K2 |
|
|
|
|
2 |
|
6 |
|
|
|
|
|
|
|
A |
4 |
C2 |
|
|
|
|
n2 |
|||
2 |
|
B2 |
|
|
|
|
|
M2 |
||
|
|
|
|
|
|
1 |
|
|
||
|
|
|
1 |
3 |
|
3 |
|
|
||
A1 |
|
|
C1 |
5 |
|
|
|
|||
|
|
|
|
4 |
|
2 |
|
|||
|
|
|
M1 |
|
|
|
|
m1 |
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
K1 |
|
|
|
С1 N1 |
|
|
|
|
|
|
|
|
А1 К1 |
|
|
||
|
|
|
|
|
|
S1 |
|
|
|
|
|
2 |
B1 4 |
N1 |
|
|
В1 М1 |
|
n1 |
|
|
|
6 |
|
|
3 |
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Рис. 1. Спосіб ребер |
|
Рис. 2. Спосіб граней |
|
|
||||
37
1.Визначаємо точку М перетину ребра піраміди AS із площиною (m n).
Укладаємо ребро AS у допоміжну фронтальнопроектуючу площину;
Знаходимо лінію 12 перетину допоміжної площини з заданою;
Визначаємо шукану точку М перетину ребра піраміди AS із площиною (m n).
2.Аналогічно визначаємо точки N, K перетину ребер BS, CS із площиною (m n).
3.Оформляємо трикутник перетину MNK з урахуванням видимості граней піраміди.
СПОСІБ ГРАНЕЙ: Побудувати трикутник MNK перетину прямої трикутної призми ABC із
площиною (m n). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Розв’язання задачі способом граней виконується в такій послідовності (Рис. 2): |
||||||||||||||||||||||||
|
1. |
Визначаємо сторону MN перетину грані ВР із площиною (m n). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Будуємо лінію 12 перетину площини грані ВР із площиною (m n). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Визначаємо точки M, N перетину прямої 12 з ребрами В и С призми АВС. |
|
|
|
|
|
|
|||||||||||||||||||
|
2. Аналогічно визначаємо точки М, K перетину ребер В, А с площиною (m n). |
|
|
|
|
|
|
|||||||||||||||||||
|
3. Оформляємо трикутник перетину MNK з урахуванням видимості граней призми. |
|||||||||||||||||||||||||
|
|
Аналізуючи розглянуті два способи визначення багатокутника перетину граного тіла |
||||||||||||||||||||||||
|
площиною, робимо висновок - спосіб ребер поглинає в собі собою спосіб граней. |
|
|
|
|
|
|
|||||||||||||||||||
|
Виділення останнього, як окремого способу, |
|
|
|
|
B2 F2 |
C2 E2 |
|
|
|
|
|
|
|||||||||||||
|
виправдано для площин-граней, що |
m2 |
A2 |
|
|
D2 |
||||||||||||||||||||
|
проекціюються в відрізок прямої, але його |
|
|
|
|
2 |
|
|
4 |
|
6 |
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
доцільно назвати способом двох ребер. |
|
|
|
|
P2 |
|
Q2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Спосіб двох ребер може застосовуватися як |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
для ребер належних, так і для ребер, що не |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
належать до однієї грані. |
|
|
|
|
|
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
СПОСІБ |
ДВОХ |
РЕБЕР: |
Побудувати |
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
багатокутник |
перетину |
прямої |
шестикутної |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
призми площиною (m n). |
|
|
|
n2 |
|
N2 |
|
|
K2 |
|
|
|
|
|
|
|
|
|||||||||
Розв’язання |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. |
Два горизонтально проекціюючі ребра, що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
m1 |
|
|
|
|
|
|
2 |
|
|
|
4 |
6 |
|
|
|
|||||||||||
|
проходять через вершини А и F, укладаємо в |
|
|
|
F1 P1 |
|
|
|
|
|
E1 Q1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
допоміжну |
горизонтально |
проекціюючу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
площину. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
Визначаємо |
проекції |
лінії |
12 |
перетину |
A1 |
M1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
допоміжної площини з заданою площиною |
|
|
|
|
|
|
|
|
|
D1 S1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
(m n). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Відзначаємо точки M, P перетину лінії 12 з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
тими ребрами призми, |
що були укладені в |
|
|
|
B1 N1 |
|
|
|
|
|
C1 |
K1 |
|||||||||||||
|
горизонтально проекуючу площину. |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4. Аналогічно знаходимо вершини N,Q на |
1 |
3 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
ребрах |
з |
двома |
ребрами, що |
проходять |
|
|
|
|
|
|
|
Рис. 3 |
|
|
|
|
|
|
|||||||
|
через вершини В, Е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5.І, нарешті, застосовуємо спосіб двох ребер
для визначення вершин, що залишилися, K, S шуканого шестикутника перетину.
6.Отримані вершини з'єднуємо, оформляючи креслення з урахуванням видимості.
Ще раз відзначимо, що спосіб двох ребер відрізняється від способу граней тим, що допоміжна площина-посередник, проходячи, через два ребра, може, як належати, так і не належати грані багатогранника.

38
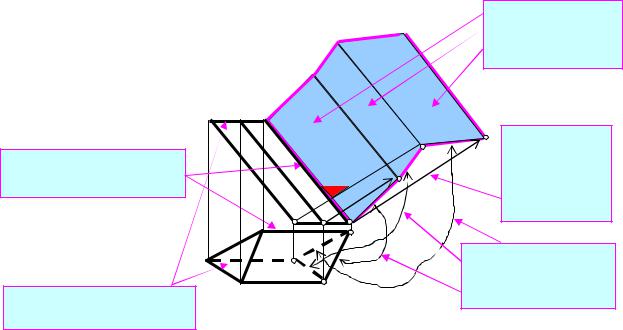
3.2. ПОБУДОВА РОЗГОРТОК ПОВЕРХОНЬ
Для конструювання інженерних геометричних форм із листового матеріалу необхідно вміти будувати розгортки поверхонь цих форм по заданих їх проекціях. На практиці досить вивчити способи побудови розгорток граних поверхонь, а для побудови розгорток кривих поверхонь використовують розгортки вписаної граної поверхні. Точність розгорток кривої поверхні регулюють кількістю граней вписаної граної поверхні.
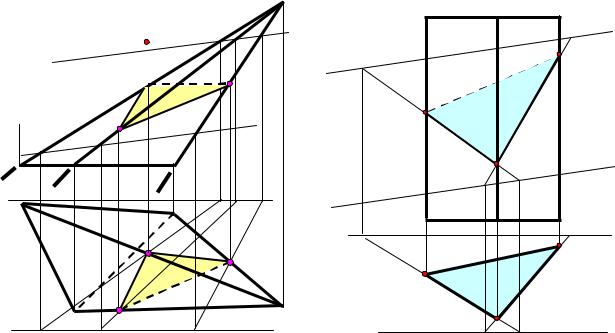
3.2.1. СПОСІБ ТРИКУТНИКІВ Спосіб трикутників (спосіб тріангуляції) можна застосувати однаково успішно для
будь-якої поверхні. Сутність цього класичного способу побудови розгорток поверхонь полягає в наступному:
1.Будуємо тріангуляцію поверхні (вписуємо в поверхню багатогранник із трикутними гранями. Багатокутні грані також розбиваємо на трикутники).
2.Визначаємо натуральні довжини усіх сторін одержаних трикутників.
Розгортка складається із чотирьох рівнобедрених
3.Будуємо трикутники із натуральних довжин сторін, стикуючи їх відповідним способом, формуючи розгортку поверхні.
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
трикутників 156 і чотирьох конічних поверхонь |
||||
|
|
|
|
|
|
|
51234. Способом прямокутного |
|
|
|
|
|
|
н.в.52 = 53 |
|
трикутника визначені |
|
|
|
|
|
|
|
натуральні величини відрізків |
||
|
|
|
|
|
|
|
||
|
|
|
|
|
н.в.5 4 = 51 |
|
51, |
52, 53, 54. Натуральні |
|
|
|
|
|
|
|
величини інших сторін |
|
|
|
|
|
|
|
|
трикутників не спотворюються |
|
|
|
|
5 |
|
|
|
на проекціях. Способом засічок |
|
6 |
|
|
2 3 |
1 4 |
|
побудовані трикутники, що |
||
|
|
|
|
визначають розгортку |
||||
|
|
|
|
|
|
|
четвертої частини перевідника. |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|||
|
|
|
4 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
5 |
|
|
|
|
|
6 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 4. Побудова розгортки перевідника6від круглого отвору5(вгорі) до квадратного отвору
(внизу).
39
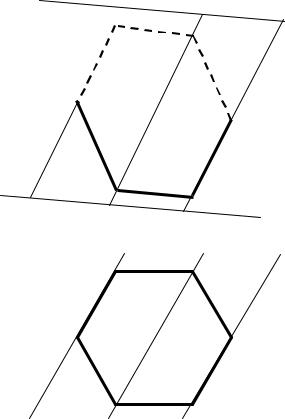
3.2.2. СПОСІБ РОЗКАТКИ
Для побудови розгорток призм, ребра яких не спотворюються на проекціях зручно застосувати спосіб розкатки. Сутність способу розглянемо на прикладі.
Задача. Побудувати розгортку призми, ребра якої не спотворюються на площинах проекцій.
Всі грані розгортки призми – паралелограми.
|
Напрямок розкатки |
Бокові ребра призми – |
перпендикулярний |
боковим ребрам |
|
фронтальні відрізки. |
призми. |
|
Зазначені стрілками відрізки рівні між собою.
Основи призми – горизонтальні трикутники.
Рис. 5. Побудова розгортки способом розкатки.
Якщо необхідно побудувати розгортку циліндра, то в нього вписують багатокутну призму, до якої застосовують спосіб розкатки. Отримані точки з'єднують не ламаною, а плавною лекальною лінією.
Достоїнство способу розкатки – простота побудов, недолік – незручність розташування на кресленні (неможливість відділення розгортки від проекцій і зображення розгортки в заданому положенні і в заданому місці креслення). Спосіб нормального перерізу позбавлений цих недоліків, він дозволяє відразу будувати розгортку на листовому матеріалі викрійки, але він вимагає невеликих допоміжних побудов (нормальний переріз призми та його натуральну величину).
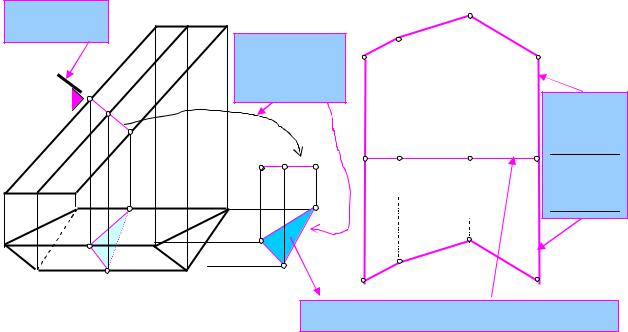
3.2.3. СПОСІБ НОРМАЛЬНОГО ПЕРЕРІЗУ
Переріз призми називається нормальним, якщо січна площина перпендикулярна бічним ребрам призми. Якщо ребра призми належать лініям рівня, то площина нормального перерізу є проекціюючою. На розгортці нормальний переріз призми розгорнеться в лінію, перпендикулярну бічним ребрам. Виходячи з цього, можна сформулювати послідовність побудови розгортки способом нормального перерізу:
1.Через довільну точку бічного ребра призми проводимо нормальну площину.
2.Будуємо переріз призми нормальною площиною.
40
3.Будуємо натуральну величину перерізу одним із відомих способів.
4.Розгортаємо багатокутник перерізу в пряму лінію.
5.Перпендикулярно до цієї лінії поводимо прямі через точки стику сторін.
6.Від точок стику по цих прямих відкладаємо натуральні відрізки бічних ребер призми.
7.Оформляємо креслення розгортки бічної поверхні призми.
Розглянемо приклад побудови розгортки способом нормального перетину (рис. 6). У нашому прикладі трикутна призма ABCDEF має бічні ребра, які не спотворюються на фронтальній площині проекцій П2. У цьому випадку спосіб нормального перерізу особливо простий у застосуванні.
|
Нормальна |
D2 |
F2 |
E2 |
|
|
F0 |
E0 |
|
|
|
|
|
|
|
|
|
||||||
|
площина |
|
|
|
|
|
|
|
|
||
|
|
|
Способом |
D0 |
|
|
D0 |
||||
|
σ2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
ППП |
|
|
|
|
|
||
|
|
1 |
|
|
визначена |
|
|
|
|
||
|
|
90˚ |
2 |
|
|
|
|
|
|
|
1D2=10D0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
3 |
|
|
|
|
|
30 |
|
2F2=20F0 |
|
|
|
|
1 |
2 |
3 |
20 |
10 |
3E2=30E0 |
||
A2 |
|
|
|
|
10 |
|
|
1A2=10A0 |
|||
B2 |
C2 |
|
|
|
|
|
|
|
|||
3 |
E1 |
|
|
|
|
|
|
2B2=20B0 |
|||
|
|
C1 |
|
|
3 |
|
|
|
3C2=30C0 |
||
|
|
|
|
|
1 |
|
|
C0 |
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
||
|
1 |
D1 |
|
|
|
|
|
|
|
|
|
|
B1 |
F1 |
|
2 |
|
B |
|
|
A0 |
||
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
A0 |
|
|
|
|
|
|
|
|
|
|
|
Периметр натурального нормального перерізу |
||||
Рис. 6. Побудова розгортки трикутної призми способом нормального перерізу.
ВПРАВИ ДЛЯ САМОСТІЙНОГО ДОСЛІДЖЕННЯ
1.З'ясувати, чи обов'язково для побудови розгорнення призми мати на проекціях натуральні величини її основ.
2.Побудувати розгортку призми загального положення, способом нормального перерізу, не переводячи її в окреме положення. Оцінити ефективність запропонованого Вами алгоритму побудови.
