Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донбасская национальная академия строительства и архитектуры

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

методичка высшая математика

.pdf

Скачиваний:

212

Добавлен:

21.02.2016

Размер:

648.96 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

прямоугольные части. При каких линейных размерах участка длина всего забора окажется наименьшей, и чему она равна?

115. Величина угла при вершине А трапеции ABCD равна α. Длина боковой стороны AB вдвое больше длины меньшего основания BC. При каком значении α величина угла BAC будет наибольшей, и чему она будет равна?

116.Найти косинус угла при вершине равнобедренного треугольника, имеющего наибольшую площадь при данной постоянной длине медианы, проведенной к его боковой стороне.

117.Из пункта А на прогулку вышел пешеход со скоростью v км/ч. После того, как он отошел от А на S км, из А следом за ним выехал велосипедист, скорость которого была на v1 больше скорости пешехода. Когда велосипедист догнал

пешехода, они повернули назад и возвратились вместе в А со скоростью v2 км/ч. При каком значении v время прогулки пешехода окажется

наименьшим, если значения S, v1 и v2 считать заданными? Чему равно это время?

118. Известно,	что	мощность	Р, отдаваемая электрическим	элементом,
определяется	по	формуле	P = E 2 R (R + r)2 , где Е –	постоянная

электродвижущая сила элемента, r – постоянное внутреннее сопротивление, R – внешнее сопротивление. Каким должно быть внешнее сопротивление R, чтобы мощность P была наибольшей? Каково значение этой мощности?

119.Боковое ребро правильной треугольной пирамиды имеет постоянную заданную длину и составляет с плоскостью основания угол α. При каком значении α объем пирамиды будет максимальным, и чему этот объем равен?

120.В конус с заданным постоянным объемом вписана пирамида; в ее основании лежит равнобедренный треугольник, у которого величина угла при

вершине равна α. При каком значении α объем пирамиды является наибольшим, и чему он равен?

Литература к задачам 111-120: [4], т.1, гл.V, §7; [6], гл.IV, §1; [9], с.358364, 439-463; [15], гл.III, §6.

Пример. Площадь поверхности сферы равна S. Какова высота цилиндра наибольшего объема, вписанного в эту сферу? Чему равен этот объем?

Пусть цилиндр образован вращением

прямоугольника ABCD вокруг диаметра MN.

Полагая AD=x, выразим объем V цилиндра

как функцию от x.

Имеем,

S = 4πOB2 ,

откуда

OB2 = S 4π.

Далее,

из

AOB

получим

= OB

−OA

то

есть

AB2 =

−

S −πx2

Тогда

объем

4π

N C

4x2 −1

цилиндра равен V (x)= πAB2 AD =

Sx −πx3

3πx2

S −

′

при

S −3πx

= 0 .

Отсюда

находим

V (x)=

; V (x)= 0

′

x =

3π (так как x>0). При 0 < x <

3π имеем V (x)> 0 , а если x > 3π ,

то

′

является

точкой

максимума и

3π

V (x)< 0 . Следовательно, x =

−π

S .

соответствует наибольшему объему V (x)==

3π

3π =

3π

ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

121-130.

Исследовать

методами дифференциального

исчисления

функцию

y = f (x)

и, используя результаты исследования, построить ее график.

121.y = x3 + 4 .

123. y = ln x −x 5 + 2 . 125. y = 3 x(x −1)2 .

127. y = ln x −x 2 − 2 .

129.	y =	x2	−3		.
		3x	2	− 2

122. y = (4 − x)ex−3 .

124.	y =	e x+3		.
124.	y =	x +	3	.
		x +	3
126.	y =	4x	2		.
126.	y =	3 + x2			.
		3 + x2
128.					x		2	+1
128.	y = ln x +				x			+1	.

130.	y =	4x3	−3x			.
130.	y =					.

Литература к задачам 121-130: [3], т.1, гл.V, §2; [4], т.1, гл.V, §2-5, 9-11; [5], т.II, р.I, гл.II; [6], гл.IV, §6,7; [9], с.471-481; [11], гл.IV, §2,3; [12], §4.1,4.2; [15], гл.III, §3-9; [21], гл.4, §27-31; [22], §4.30-4.33.

Пример. y = x2 −5 . x −3

1.Область определения: x (−∞;3) (3;+∞).

2.f (− x)≠ f (x), f (− x)≠ − f (x), -следовательно, функция не является ни

четной, ни нечетной, то есть это функция общего положения.

3. Исследуем характер точки разрыва x = 3 и поведение функции вблизи этой точки:

lim

x2 −5

= lim

(3 −ε)2 −5

lim

= −∞,

x −3

3 −ε −3

−ε

x→3−ε

ε→0

lim

x2 −5

= lim

(3 + ε)2 −5

lim

= +∞.

x −3

3 + ε −3

x→3+ε

ε→0

Таким образом, в точке x = 3 функция терпит разрыв второго рода,

а прямая x = 3 является вертикальной асимптотой.

4. Определим уравнение наклонной асимптоты:

y = kx +b , где

f (x)

−5

1−5 x2

k =

lim

=1,

−3)

−3 x

x→±∞ x

x→±∞ x(x

→±∞

−5

− x

+3x

b =

lim

[f (x)

− kx]=

lim

− x

lim

= 3 .

x −3

x→±∞

x −3

x→±∞

Итак,

y = x +3 - наклонная асимптота.

Проверим, как расположен график функции по отношению к

асимптоте при x → ±∞, то есть лежит он выше или ниже.

Так как значения функции определяются выражением

y =

−5

, а

x −3

ординаты точек асимптоты - функцией y = x +3 то

y − y =

x2 −5

−(x +3)=

x −3

При

x → +∞:

y − y > 0 ,

следовательно,

график функции лежит над

асимптотой.

При

x → −∞:

y − y < 0 ,

следовательно,

график функции лежит под

асимптотой.

5. Определим критические точки.

′

2x(x −3)− x2 +5 x2 −6x +5

(x −3)2

= (x −3)2

y′ = 0 при x2 −6x +5 = 0 , то есть при

x =1 и

x = 5 , -

других критических точек в области определения

функции нет. Значения функции в критических точках:

y(1)

= 2 , y(5)=10 .

6. Найдем вторую производную:

y′

(2x −6)(x −3)2 − 2(x −3)(x2 −6x +5)

−6x +5

(x −3)

y′ ≠ 0 , следовательно, точек перегиба нет.

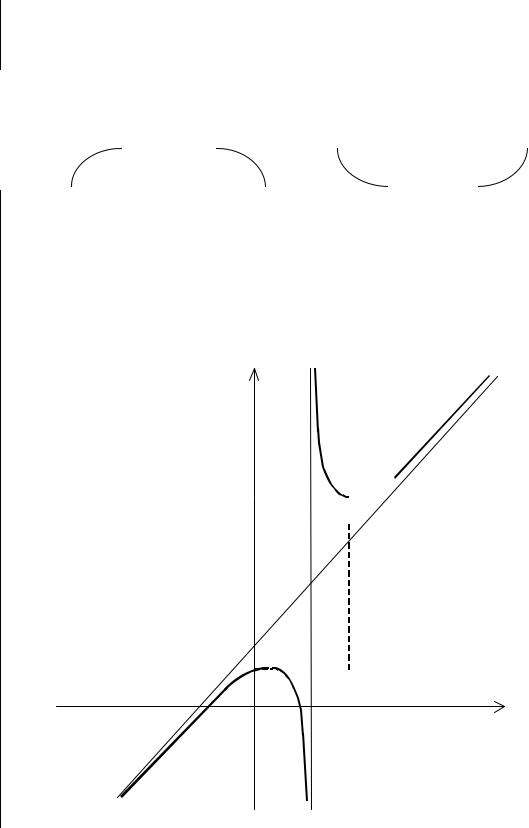
7. Внесем все полученные данные в таблицу, определим поведение функции на различных участках и построим график.


x	(−∞;1)		1	(1;3)	3	(3;5)		5	(5;+∞)
y′	+		0	-		-		0	+
y′′	-		-	-		+		+	+
y			2					10
			max					min
	Положительные значения первой производной соответствуют
промежуткам		возрастания, отрицательные –					промежуткам убывания.

Положительные значения второй производной соответствуют промежуткам вогнутости функции, отрицательные – промежуткам выпуклости. Точка, в которой возрастание функции сменяется убыванием, является точкой максимума, а точка, в которой убывание функции сменяется возрастанием – точкой минимума.

10 y=x+3








O 1 3 5			x

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

131-140. Дана функция z = f (x, y). Показать, что

∂z

∂2 z

F x; y; z;

;

= 0.

∂x ∂y

∂x

∂y

∂x∂y

z =

∂z

131.

F = y

∂x

− x

∂y .

(x2 + y2 )2

1 xy

∂z

2 ∂z

132.

z =

+ e

F = xy

∂y

− x

∂x

− y

133.

z = e y cos yex2

2 y 2

, F = (x2 − y2 )∂z

+ xy

∂z − xyz .

∂x

∂y

134.

z = x

, F = x

2 ∂2 z

+ 2xy

∂2 z

+ y

∂2 z

−2z .

∂x2

∂x∂y

∂y2

135.

z = x arcsin(x + y)+ yex+ y , F = ∂2 z

− 2

∂2 z

+ ∂2 z .

∂x∂y

∂x2

∂y2

136.

z = ln(x − 2y)+ ex+2 y , F = ∂2 z − 4 ∂2 z .

∂y2

∂x2

137.

z = ln

x2 + y2 , F = ∂2 z

+ ∂2 z .

∂x2

∂y2

138.

z =

−x2 16 y

, F =

∂z

− 4

∂2 z

∂y

∂x2

139.

z = x2arctg

, F = x

∂z

+ 2 y

∂z

− 2z .

∂x

∂y

140.

z =

+ y

F =

∂z

−

∂z

+ 4x

∂2 z

− 4 y

∂2 z

− y

∂y

∂x

∂x2

∂y2

Литература к задачам 131-140: [3], т.1, гл.VI, §2; [4], т.1, гл.VIII, §5,10,12; [5], т.III, р.I, гл.II, §1,4,10; [6], гл.IX, §3,4; [9], с.499-535; [11], гл.VII, §2; [12], §6.2,6.3; [15], гл.VI, §3,5,7; [21], гл.4, §3, 13, 16; [22], §4.3, 4.13, 4.16.

Пример. z = yex2 −y 2 , F = y2 ∂∂xz + xy ∂∂yz − xz .

При нахождении частной производной по одной из переменных со второй переменной обращаемся как с константой:

∂∂xz = 2xyex2 −y 2 , ∂∂yz = ex2 −y 2 −2y2ex2 −y 2 .

Подставляем найденные значения в функцию F:

F = 2xy3ex2 − y 2 + xyex2 − y 2 − 2xy3e x2 − y 2 − xyex2 − y 2 = 0,

что и требовалось доказать.

141-150. Найти наименьшее и наибольшее значения функции z = f (x; y) в замкнутой области D, заданной системой неравенств. Сделать чертеж области D.

141.	z = 5x + y − x2 + 2y2 ,	x ≥ 0, y ≤ 0, 3x − 4y ≤12 .
142.	z = x2 − y2 + 2x + 4,	x ≥ −2, y ≥ −1, y ≤ −x
143.	z = 3y2 − xy +5 ,	y2 −1 ≤ x ≤ 3 .
144.	z = x2 − 2xy − y2 + 2,	x ≥ −1, y ≥ −1, x + y ≤ 2 .
145.	z = 6 + 4xy + 2x2 + y2 ,	−2 ≤ x ≤ 2, −1 ≤ y ≤ 3.
146.	z = 2x2 − xy + 6 ,	x2 ≤ y ≤ 4 .
147.	z = 2x + y − 2x2 + 2y2 ,	x ≤ 2, y ≥ x −1, y ≤ 2 .
148.	z = 6 + x − y + xy + x2 ,	−3 ≤ y ≤ −1, x −3 ≤ y ≤ x .
149.	z = 2x2 + xy + y2 + 7 ,	y ≥ −x, y ≥ x, y ≤ 2 .
150.	z = 2x + xy + y2 +1,	y ≥ 2x −12, y ≥ −x, y ≤ 0 .

Литература к задачам 141-150: [3], т.1, гл.VI, §4; [9], с.550-568; [11], гл.VII, §4; [15], гл.VI, §9,10; [22], §4.38.

Пример. z = 4 + x2 + y2 , y ≥ 0, x ≤ 0, y ≤ x +1.

Необходимо найти критические точки функции и сравнить ее значения в этих точках со значениями функции на границах области.

Критические точки:							y
Критические точки:
	∂z	= 0,
	∂x	= 0,	2x = 0,	x	= 0,
	∂x		2x = 0,	x	= 0,		B
	∂z				= 0.		B
	∂z	= 0,	2 y = 0,	y	= 0.			1
	∂y							1
	∂y					y=x+1
z(0;0)= 4.						y=x+1
На границе АВ, заданной уравнением
y = x +1, имеем:
z = 4 + x2 +(x +1)2 = 2x2 + 2x +5 .						A		C
Получили функцию одно переменной.						-1		x
Теперь найдем ее критические точки и
сравним		значения функции			в них со

значениями на границе отрезка АВ (то есть в точках А и В), - тем самым можно найти максимальное и минимальное значения функции на отрезке

АВ.

∂z		= 4x + 2					= 0 x = −			1	, при этом y = x +1 =	1	.
∂x		= 4x + 2					= 0 x = −			2	, при этом y = x +1 =	2	.
∂x						1		1		2		2
						1		1
Точка −							;		принадлежит области D, причем
Точка −						2	;	2	принадлежит области D, причем
						2		2
			1		1			9
z	−			;		=			.
z	−		2	;		=		2	.
			2		2			2

Значение функции в т. А: z(−1;0)= 5 .

Значение функции в т. В: z(0;1)= 5.

Таким же образом исследуем функцию на двух других границах. На границе АС, заданной уравнением y = 0 , имеем:

z = 4 + x2 ,

∂∂xz = 2x = 0 x = 0 , при этом y = 0 ,

z(0;0)= 4 - критическая точка совпадает с граничной т.С. На границе ВС, заданной уравнением x = 0 , имеем:

z = 4 + y2 , - теперь уже имеем функцию только переменной у. ∂∂yz = 2 y = 0 y = 0 , при этом x = 0 ;

z(0;0)= 4 - значение в этой точке уже было рассчитано.

Далее, выбираем из всех полученных значений функции z наименьшее и наибольшее:

zmin = z(0;0)= 4 ,

zmax = z(0;1)= z(−1;0)= 5.

НЕОПРЕДЕЛЁННЫЙ И ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛЫ

151 – 160. Найти неопределённый интеграл. В двух первых примерах [a) и б)] проверить результаты дифференцированием.

151.	а) ∫	dx		;	б) ∫ln(x2 +1)dx
		(2x +1)3 ln	2
				(2x +1)

в) ∫	4x −	x2 −12	dx ;	г)
	x	3
		+ 8
152. а) ∫		dx	;	б)

cos2 x tg 3 x

∫

dx	;
5 + 2 sin x + 3cosx

1 − x arcsin xdx ;

в) ∫

4x + 2

dx ;

г) ∫

x +1

dx ;

x +

+ 4x

153. а) ∫ arcsin5 2x dx ;

б) ∫x sin x cos xdx ;

1− 4x 2

в) ∫

5xdx

;

г)

∫sin4 x cos5 xdx ;

+ 3x

− 4

154. a) ∫

;

б)

∫x3−4 x dx ;

+ x

)arctg

в) ∫

x3 + x2 − x − 3

dx ;

г)

− x

155.

а) ∫e4−x2 xdx ;

б)

в) ∫

2x2 − 7x +10

dx ; г)

(x −1)(x

− x

+ 4x − 4)

156.

а) ∫

x −

dx ;

б)

в) ∫

x2 + 2x + 4

dx ;

г)

+ 4

157.

а) ∫

cos3 2x sin2xdx ;

б)

в) ∫

x 3 −

2x +5

dx ;

г)

−1

158.

а) ∫

x − 5

dx ;

б)

4 − 9x2

∫ 2 sin x + 3cosx + 3 ;

∫arctg 5x dx ;

∫		x − 3 x
	3 x − 6 x −1dx			;
∫ln		2 − x	dx ;

		2 + x
∫	3cos3 x
			dx ;
	sin4 x
∫	x arcsin x dx ;
		1− x2
∫		dx		;
	3sin x − 4 cos x

∫(x + 6) cos4xdx ;

в) ∫

(2x + 3)dx

x + x + 3 x2

;

г)

∫

x(1+ 3 x)

dx ;

(x −1)(x3 − x2 + 4x − 4)

159. а) ∫

cos xdx

;

б) ∫ arccos x dx ;

3 − sin x

1+ x

в) ∫

− 8x

dx ;

г) ∫cos3 x sin8 xdx ;

+ 4x

160. а) ∫

5xdx

;

б)

∫

x ln xdx ;

7x 2 −1

в) ∫

x 3 − x −

dx ;

г)

∫

xdx4 .

4 2

− x

Литература к задачам 151-160: [3], т.2, гл.I; [4], т.1, гл.X, §1-13; [5], т.II,

р.II, гл.I; [6], гл.XIII; [9], с.575-716; [10], гл.1; [11], гл.V, §1; [15], гл.IV; [21], гл.5, §1-10; [22], §5.1-5.14, 5.17.

Пример.

а)

xdx

x2 = t

xdx =

arctgt +C =

arctgx2 +C .

∫

x4 +

2 +

2xdx

= dt

Проверка:

xdx

arctgx2 +C) =

d(arctgx2 ) + dC =

2xdx =

1+ x4

б) ∫

xdx

u = x,

du = dx

dv =

v = ∫

= −ctgx

sin

Применим формулу интегрирования по частям

= −xctgx + ∫ctgxdx = −xctgx + ln

sin x

+ C .

Проверка:

xdx

d (−xctgx + ln

sin x

+ C) = −d (xctgx) + d (ln

sin x

) = −ctgxdx +

sin2

+ ctgxdx =

xdx

sin2 x

в)

∫

+ 3x

Разложим подынтегральную дробь на сумму простейших:

Cx + D

x4 + 3x2

2 (x2 + 3)

x2 + 3

1 = Ax(x2 + 3) + B(x2 + 3) + x2 (Cx + D)

1 = (A + C)x3 + (B + D)x2 + 3Ax + 3B

A + C = 0,

C = 0,

D = −1 3,

B + D = 0,

3A = 0,

A = 0,

3B = 1,

B =1 3.

∫

2 =

∫ dx2 −

∫

2dx

= −

−

1 arctg

+ C .

+ 3x

3 3

= t,

sin x =

г)

∫

1 + t

8 − 4 sin x + 7 cos x

cos x =

1 − t 2

dx =

2dt

1 + t 2

= ∫

2dt

= ∫

2dt

= ∫

2dt

7(1 − t

)

+8t

−8t + 7 − 7t

(1 + t

2 )(8 −

)

−8t +15

1 + t 2

t −4 = z

−1

−5

= 2∫

= ln

+C = ln

+C =ln

+C .

(t −

−1

dt = dz

−1

−

−3

x +

1+ x

1 + x = t 6

(t 6 −1+ t 3 )

д) ∫

dx = dx = 6t

∫

= 6∫(t

+ t

− t

)dt =

1 + x

x = t 6 −1

= 6

t10 + 6 t 7

−

6 t 4

+ C =

3 6

(x +1)10 +

6 6

(x +1)7 −

3 6

(x +1)4 + C =

3 3

(x +1)5 +

6 6

(x +1)7

−

3 3

(x +1)2

+ C .

cosx = t

е) ∫cos2 x sin5 xdx =

= −∫t 2 (1− t 2 )2 dt = −∫t 2 (1− 2t 2 + t 4 )dt =

− sin xdx = dt

= −∫

− 2t

+ t

)dt

= −

−

+ C

= −

cos x

cos

x −

cos x

+ C.

161 – 170. Вычислить несобственный интеграл или доказать его

расходимость.

∞

161. ∫

162. ∫x3e−x2 dx .

x(ln x)

xdx

∞

2 + xdx

163. ∫

164. ∫

x −1

∞

xdx

xdx .

165. ∫

166. ∫

(1+ x)

x − 3

xdx .

∞

167. ∫

168.

∫

4 − x2

−∞ (x

+ 2x +

−1

169. ∫x ln xdx .

170.

∫

x + 3

−3

Литература к задачам 161-170: [3], т.2, гл.II, §2; [4], т.1, гл.XI, §7; [5], т.II, р.II, гл.II, §8; [6], гл.XIV, §4; [9], с.756-770; [10], §2.6; [11], гл.V, §4; [15], гл.V, §10; [21], гл.6, §9; [22], §6.11.

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.02.201610.58 Mб113Метод_КБ_2010.doc
#
21.02.20165.45 Mб12Метод_передачи_2012.doc
#
21.02.2016378.37 Кб13Метод_указ_УПП_контр.раб.doc
#
21.02.2016612.16 Кб8Методика кред модульн критерии оценок.pdf
#
13.08.20192.74 Mб48Методичка ВНС.DOC
#
21.02.2016648.96 Кб212методичка высшая математика.pdf
#
21.02.2016153.6 Кб21Методичка для заочников по упр. персоналом.doc
#
21.02.201611.89 Mб252Методичка ЖБК_укр.pdf
#
21.02.2016280.3 Кб8методичка иностран.яз..pdf
#
21.02.2016353.79 Кб5методичка ист заоч 2011.doc
#
21.02.2016453.12 Кб10МЕТОДИЧКА КУЗНЕЦОВА КОРП,УПР,.doc