Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донбасская национальная академия строительства и архитектуры

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

методичка высшая математика

.pdf

Скачиваний:

211

Добавлен:

21.02.2016

Размер:

648.96 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

		Так как		X3		= t		94 , то i3				7		,−	3	,	6
		Так как		X3		= t		94 , то i3			=			,−		,	94	.
													94		94		94
		Итак, λ1 = −3 , λ2 = −2 , λ3 = 8,
	i1 = {0,0,1}, i2 =				X		2		1	,	1	,		18		i3		7	,−		3	,	6
	i1 = {0,0,1}, i2 =						2	=	326	,	326	,		326	,	i3	=	94	,−		94	,	.
					X2				326		326			326				94			94		94
			ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
61-70. Найти пределы функций, не пользуясь правилом Лопиталя.
61. а)		lim	1+ 4x	+ x2		;					б)		lim		1 + 2x −			1 − x		;
61. а)		lim	3x2	+ 2		;					б)		lim				2x			;
		x→∞	3x2	+ 2									x→0				2x

в)

62.а)

в)

63.а)

в)

64.а)

в)

65.а)

в)

66.а)

lim	cos4 x −cos2 x	;
	3x2
x→0

lim	6x4 + 2x	3 +8x	;
	12 + 7x4
x→∞

lim

2 − 2cos x

;

x→0

3x2

lim

1 + 4x

;

x→∞ 2x −5

lim

arcsin 2x

;

tg3x

x→0

lim

3x3 +5

;

x→∞ 2 + x + x3

lim

;

x→0 arctg4x

lim

4 + x + x

;

x→∞ 16x2 +11

lim

1−cos 6x

;

x→0

sin 2 4x

lim

2 +5x + 7x2

;

x→∞ 3 +5x + 2x2

г)

б)

г)

б)

г)

б)

г)

б)

г)

б)

lim 1+−x 2x . x→∞ x 3

2 − 4 − x2 lim 3x2 ;

x→0

lim (x + 2)[ln(x + 4)−ln(x −1)].

x→∞

lim	9 − x −3	;
x→0	3x

lim (x −1)[ln(3x −5)−ln(3x + 2)].

x→∞

lim	3 − 25 − x2
		x −	4		;
x→4				x
		2x +5
				2	.


xlim→∞ 2x +8
lim		x + 2x	2		;
		1+ 4x
x→0			−1

lim (1+3x)4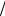x .

x→0

lim	1 + 4x − 1	+ 2x ;
x→0	x2 + 4x

	x3ctg5x			2x
в) lim		;	г) lim (5 − 2x)x−2 .

x→0 tg 2 (x 5)			x→2

67.а)

в)

68.а)

в)

69.а)

в)

70.а)

в)

lim		4x +11	;
lim			;
x→∞		1 +8x
lim		x(1−cos 2x)					;
lim							;
x→0 tg6x sin 2 3x
		2 +11x +			9x3
lim									;
lim					+8				;
x→∞ x3 +3x2					+8
lim	tg 2 (x 4)			;
lim	1−cos x			;
x→0	1−cos x
lim		x2 +5				;
lim	1 + x + 2x2					;
x→∞	1 + x + 2x2
lim	arcsin 4x			;
lim		tg2x		;
x→0		tg2x
		2 + 4x2 + x6
lim								;
lim					+3			;
x→∞ x6 + 5x5					+3

lim ctg 2 2x sin 2 5x ; x→0

б)

lim

x −3 x ;

x→9 x2 −9x

г)

lim (3x − 2)

x2−1

x→1

б)

lim

;

x→0 4 −

16 + x2

2x+1

г)

lim (x −3) 4−x .

x→4

б)

lim

3 −

4 + x

;

x→5

2x −10

3−x2

г)

lim

1 +

x→0

б)

lim

1 −

2 − x2

x2 −1

;

x→1

x+5

г)

lim (7 − 2x)2x−6 .

x→3

Литература к задачам 61-70: [3], т.1, гл.IV, §4,5; [4], т.1, гл.II, §1-7,11; [5], т.I, р.II, гл.III, §10-14; [6], гл.III, §2,3; [9], с.300-343; [11], гл.II, §1,3; [15], гл.I, §6-9; [21], гл.3, §4; [22], §3.4.

Пример.

3x4

+ x2

3 +

+ 2

∞

а)

lim

= lim

= 3 .

2 + x + x4

x→∞

∞

x→∞

Здесь

мы

разделили

числитель и знаменатель на максимальную

степень х, то есть на x4 . Дробные слагаемые в числителе и знаменателе стремятся к нулю при x → ∞.

б) lim		x2				0	=
б) lim	2			2	=		=
x→0 1 − x	2	−	1 − 2x	2	0
x→0 1 − x		−	1 − 2x

+ 1 − 2x

1 − x

= lim

x→0

1 − x

−

1 − 2x

1 − x

1 −

1− x

+ 1− 2x

1− x

1−2x

= lim

1− x2 −1+ 2x2

= lim

x→0

= lim

1− x2 +

1− 2x2 =1+1 = 2 .

x→0

Здесь домножили числитель и знаменатель на сопряженное к

знаменателю, чтобы получить в знаменателе разность квадратов.

в)

lim

(1−cos 4x).

x→0

sin 2 3x

Так как

1−cos 2α = 2sin 2 α, sin α ~ α при α → 0 , то

lim

(1−cos 4x)= lim

2sin 2 2x

= lim

2 (2x)2

2 4

(3x)2

9x2

x→0

sin 2 3x

x→0

−7 = t,

4(t+7)

г)

lim (15 −2x)

x−7

= lim (15 −2(t + 7))

t+7−7

= x

→ 7 t → 0,

x→7

= t + 7

t →0

−2t

4t+28

(−2t )

= lim (1− 2t)

(1− 2t)

= lim (1− 2t) t

−2t

= lim

−2t

t →0

lim [−2(4t+28)]

→0

lim

(−8t −56)

= lim (1− 2t)−2t

= et→0

= e−56 .

t →0

Здесь необходимо было использовать второй «замечательный» предел:

lim (1+ x)1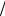x = e . Для этого пришлось сначала перейти к новой

x→0

переменной t, которая стремится к нулю при x → 7 .

71-80. Задана функция y = f (x). Найти точки разрыва функции, если они существуют. Сделать чертеж.

	x −2,		x ≤ −1;
71.	f (x)= x2 +1,		−1 < x < 2;
	2x +1,		x ≥ 2.

	3x − 4,		x <1;
73.	f (x)= x +3,		1 ≤ x < 6;
	x −3,		x ≥ 6.

	− x,	x <1;
75.	f (x)= x2 ,	1 ≤ x ≤ 3;
	−2x +15,			x > 3.

	sin x,		x ≤ 0;
77.	f (x)= 2x,	0 < x < 2;
			x ≥ 0.
	4 − x,		x ≥ 0.
	cos x,		x ≤ −π 2;
79.	f (x)= x + π 2,			−π 2 < x ≤1;
		x	>1.
	x2 ,	x	>1.

		x,	x < 0;
72.	f (x)=	sin 2x,		0 ≤ x < π;

			− 4,	x ≥ π.
		2x	− 4,	x ≥ π.
		2x +3,		x ≤ −2;
74.	f (x)= −(x +3)2 ,				−2 < x ≤ 0;
			x > 0.
		x,	x > 0.

		2(x +1), x ≤ −2;
76.	f (x)= −		2 − x,		− 2 < x ≤ 2;
				x > 2.
		− x +1,		x > 2.
			+ 6,	x < −π 4;
		3x	+ 6,	x < −π 4;
78.	f (x)=	tgx, − π 4 ≤ x < π 3;

			3 π,		x ≥ π 3.
		3x	3 π,		x ≥ π 3.
		−2 +3x,			x <1;
80.	f (x)= x2 + 2,			1 ≤ x ≤ 3;
		4x	−1,	x > 3.

Литература к задачам 71-80: [3], т.1, гл.IV, §6; [4], т.1, гл.II, §9; [5], т.I, р.II, гл.III, §15,16; [6], гл.III, §4; [9], с.343-358; [11], гл.II, §2; [12], §2.8; [15], гл.I, §10; [21], гл.3, §5; [22], §3.4.

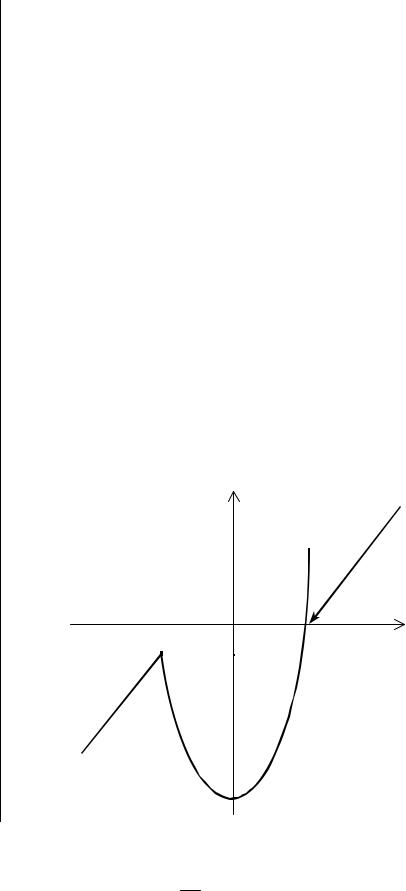
x +1, x < −3;
Пример. f (x)= x2 −11,	−3 ≤ x ≤ 4;
x −4,	x > 4.

Очевидно, в каждом из трех интервалов функция является непрерывной, поэтому исследуем функцию на непрерывность в точках x = −3 и x = 4 , в которых она меняет свой вид. Для этого вычислим пределы слева и справа, а также значения функции в этих точка. Если для одной точки все эти величины совпадают, то функция непрерывна, в противном же случае она терпит разрыв, характер которого определяется из значения пределов.

При расчете предела слева в точке x = −3 необходимо учесть, что в этом интервале f (x)= x +1, поэтому

lim	f (x)= lim	(x +1)= lim (−3 −ε +1)= −2 .
x→−3−0	x→−3−0	ε→0

При расчете же предела справа в точке x = −3 имеем f (x)= x2 −11,

						45
поэтому	f (x)=				(x2 −11)= lim ((−3 + ε)2 −11)= −2.
lim			lim
x→−3+0			x→−3+0			ε→0
Кроме	того,		f (−3)= (−3)2 −11 = −2 , так как, по условию,
f (x)= x2 −11 при x = −3 . Итак,
lim	f (x)=		lim		f (x)= f (−3),
x→−3−0			x→−3+0
следовательно, функция y = f (x) непрерывна в точке x = −3 .
Аналогично,					(x2 −11)= lim ((4 −ε)2 −11)= 5 ,
lim	f (x)=		lim
x→4−0		x→4		−0		ε→0
lim	f (x)=		lim		(x − 4)= lim (4 + ε − 4)= 0 ,
x→4+0		x→4		+0		ε→0
f (4)= (4)2 −11 = 5.
Таким образом,
lim	f (x)≠		lim		f (x),
x→4−0		x→4		+0		функция y = f (x) терпит разрыв первого
следовательно, в точке				x = 4

рода.

Сделаем чертеж. При этом если одна из ветвей функции не задана в точке, то будем отмечать ее стрелкой

	y
5			y=x-4


-3	O





			x








		4






		-2
		-2

y=x+1

y=x2-11

-11

ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ

81-90. Найти производные dydx данных функций.

81.а)

г)

82.а)

г)

83.а)

г)

y =

;

б)

y = cos2 e3x ;

3 1− x2

y = xsin x ;

д) x + y + arcsin

= 0

y = 4

1− x

;

б)

y = tg

+ 2ln sin x ;

1+ x

e x

д) x

+ xy

− y

= 0 .

y = (tgx)

;

y = x

− x

;

б)

y = cos

1+ x

;

y = x x ;

д)

= arctg

в) y = arctg ln 1x ;

в) y =		1			;
	etgx			+ 2

в) y = arctg		1		+ x		;
			1	− x

84.а)

г)

85.а)

в)

д)

86.а)

г)

87.а)

г)

88.а)

г)

89.а)

г)

y = 3

1+ x3

;

б) y =

sin

2 x

;

1− x3

sin x2

y = x

1 xy

= x .

; д)

+ e

y =

;

б)

y = ln tg

−cos x ln tgx ;

a2 − x2

y =

(ln3 x +3ln2 x + 6 ln x + 6); г) y = (sin x)cos x ;

yex + xsin y + xy = 0.

y =

x + x +

x ;

б)

y = tg

−ctg

;

y = xarctgx ;

д) e3xy − x3 y3 =1.

y = 3 3 x + x2 −

;

б) y = tg 3 sin 2 x ;

y = (ln x)sin x ;

д)

x + y −2sin xy = 0 .

y =

x2 + 4 +

;

б) y =

cos x

;

y = (x +1)2x ;

4x + 2x3

2sin 2 x

д) xy + x2 y2 −e2xy = 0 .

в) y = arccos 1x ;

в) y = ln3 x2 ;

в) y = ln(x + e5x );

в) y = arctg ctg 2 x ;

y =	2 + x	;	б) y = 3cos2 3x ;	в) y = arctg x2 −1 ;
	x2 + 2x + 4
y = (tgx)cos x ;		д)	arctg xy −exy = 0 .

									47
90. а)	y =	1+ x2	;	б)	y = ln	1−cos x		;	в) y = arccos x ;
		1+ x				1	+ cos x

г)		e x	;	д) xsin y − y cos x = sin xy .
	y = (ln x)

Литература к задачам 81-90: [3], т.1, гл.V, §1; [4], т.1, гл.III, §2, 9, 11, 12, 15, 16, 18; [9], с.358-407; [11], гл.III, §2; [15], гл.II, §1-7,9,10; [21], гл.4, §4-7, 19; [22], §4.5, 4.7, 4.19.

Пример.

а)

y = x +

1− x2 arccos x .

1− x

′

1− x

′

y′ =1+

arccos x +

(arccos x)

=1+ arccos x

(1− x2 )′ −

1− x2 =1− 2x arccos x

−1 = − x arccos x .

2 1− x2

1− x2

2 1− x2

1− x2

y = ln arcsin

1 .

Применим правило дифференцирования сложной функции:

если y = f

(u), а u = ϕ(x), то y′x = fu′

ϕ′x . Тогда получим:

y′ =

′

1 ′

arcsin

1 2

1−

−

= −

x −1

arcsin

1 −

arcsin

= −

2x x −1 arcsin

y = x x

Так как и основание, и показатель степени зависят от х, то сначала прологарифмируем обе части равенства, а после этого возьмем производные от обеих частей и выразим y из полученного уравнения:

ln y = ln x x ;

ln y = x ln x (свойство логарифмической функции);

(ln y)′ = (x ln x)′;

1	y′ = ln x + x	1	(так как дифференцируем по	х, а у зависит от х, то
y	y′ = ln x + x	x	(так как дифференцируем по	х, а у зависит от х, то
			ln y(x) дифференцируется как	сложная функция).

y′ = y (ln x +1)= x x (ln x +1). d) x3 y + e y = 0 .

Так как y = f (x) задана неявно, то продифференцируем левую и правую части, помня, что y = y(x):

3x2 y + x3 y′+ e y y′ = 0 .

Выражая отсюда y′, получаем:

(x3 + e y ) y′ = −3x2 y ;

y	′		3x2 y
		= − x3 + e y .

91-100.	Найти	dy	и	d 2 y
		dx		dx	2

б) x = ϕ(t), y = ψ(t).

91.а) y = x ln2 x ,

92.а) y = x arcsin x ,

93.а) y = tg 2 x ,

94.а) y = e−x3 ,

95. а) y =	x	,
	1− x2

96.а) y = sin x ,

97.а) y = esin x ,

98.а) y = ln tgx ,

99.а) y = ln2 x ,


для	заданных		функций: а) y = f (x);
б) x = 3t −t3 , y = 2t −t 2 .
б)	x = et sin t ,	y = et cost .
б)	x = a cost ,	y = a sin t .
б)	x = sin3 t ,	y = cos3 t .
б) x = t 2 + 4, y = t3 −t .
б) x = e2t , y = e3t .
б) x = 2(t −sin t),			y = 2(1−cost).

б)	x = 2t −t 2 , y = 3t −t3.
б)	x = a(cost +sin t), y = a(sin t −cost).

100. а) y =	sin x	,	б)	x = t 2 , y =	t3	−t .
	x			3

Литература к задачам 91-100: [3], т.1, гл.V, §1; [4], т.1, гл.III, §22, 24; [9], с.418-423; [11], гл.III, §5; [15], гл.II, §8,10; [21], гл.4, §12; [22], §4.12.

Пример. а) y = x

1+ x

б) x = cos

2 t

y = t

−sin t .

а) y

′

1+ x

1+ 2x2

1+ x2 =

1+ x2 ,

4x 1 + x2 −

x + 2x3

x(3 + 2x2 )

′′

1 + x2

3x + 2x3

1 + x2

= (1 + x2 )3 2 = (1 + x2 )3 2 .

б) Так как

yt′

, а

xt′

xt′ = −cos

sin

yt′ =1

−cost =

2sin

, то

2sin

2 t

= −

= −2tg

cos

sin

Чтобы найти вторую производную по х, необходимо

продифференцировать

по

полученное

значение dy dx , являющееся

опять таки функцией переменной t, поэтому

′

d 2 y

d dy

dx2

xt′

dx dx

′

−2tg

′

, следовательно,

= −

cos2 (t 2)

d 2 y

− cos2 (t 2)

dx2

− cos(t

2)sin(t

sin(t 2)cos3(t 2)

101-110. Найти наименьшее и наибольшее значения функции y = f (x) на отрезке [a;b].

101.	y = x5 −5x ,	[−2;2].
102.	y = 4 −3x ,	[−1;1].
103.	y = 3x3 −36x +1,	[1;3] .
104.	y = 2x4 + x ,	[−2;1].

105.	y =	x	−cos x ,			[−	π;	π	].
								4
	2						4
106.	y = x6 −2x3,					[−1;1].
107.	y = x −tgx ,					[−	π;	π	].
	y = 3x5 −20x3 + 2 ,						6	3
108.						[−1;2] .
109.	y = 3sin x −			3	x +1,	[0;	π].

	2						2
110.	y = 6x7 −21x2 +5,					[−1;1].

Литература к задачам 101-110: [3], т.1, гл.V, §2; [4], т.1, гл.V, §6; [5], т.II, р.I, гл.II, §3; [6], гл.IV, §6; [9], с.439-449; [11], гл.IV, §2; [12], §4.1; [15], гл.III, §5.

Пример. y = 3x2 + 6x +1, [−2;0] .

Для нахождения наименьшего и наибольшего значений функции на отрезке необходимо определить значения функции в точках экстремума (если такие существуют на заданном сегменте) и сравнить эти экстремальные значения со значениями функции на границах отрезка, после чего выбрать из всех значений минимальное и максимальное.

Найдем критические точки:

y′ = 6x + 6 , y′ = 0 x = −1; −1 [−2;0]; y(−1)= −2 .

Значения на границах: y(− 2)=1, y(0)=1.

Таким образом,

ymin = y(−1)= −2 , ymax = y(− 2)= y(0)=1.

111.Из квадратного листа жести со стороной a вырезают по углам одинаковые квадраты со стороной b и сгибают так, чтобы получился открытый сверху параллелепипед. При каком значении b полученный параллелепипед будет иметь наибольший объем, и чему этот объем равен.

112.В прямоугольный треугольник с гипотенузой a и углом α вписан прямоугольник, основание которого лежит на гипотенузе. Каковы должны быть длины сторон прямоугольника, чтобы его площадь была наибольшей? Чему равна эта площадь?

113.Боковые стороны и меньшее основание трапеции имеют одинаковую длину а. Найти размер ее большего основания, при которой площадь трапеции была бы наибольшей, и вычислить эту площадь.

114.Требуется огородить забором прямоугольный участок земли площадью в S квадратных метров и разделить затем этот участок на три равные

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.02.201610.58 Mб102Метод_КБ_2010.doc
#
21.02.20165.45 Mб12Метод_передачи_2012.doc
#
21.02.2016378.37 Кб13Метод_указ_УПП_контр.раб.doc
#
21.02.2016612.16 Кб7Методика кред модульн критерии оценок.pdf
#
13.08.20192.74 Mб38Методичка ВНС.DOC
#
21.02.2016648.96 Кб211методичка высшая математика.pdf
#
21.02.2016153.6 Кб21Методичка для заочников по упр. персоналом.doc
#
21.02.201611.89 Mб247Методичка ЖБК_укр.pdf
#
21.02.2016280.3 Кб8методичка иностран.яз..pdf
#
21.02.2016353.79 Кб5методичка ист заоч 2011.doc
#
21.02.2016453.12 Кб10МЕТОДИЧКА КУЗНЕЦОВА КОРП,УПР,.doc