
методичка высшая математика
.pdf
31
AB =  (−1)2 +32 + (−3)2 =
(−1)2 +32 + (−3)2 =  19 .
19 .
2) Угол между ребрами AB и AD равен углу между соответствующими векторами и находится по формуле:
cos ϕ = AB AD .
AB AD
Координаты вектора AD равны:
AD = {2;2;−3}, AD =  4 + 4 +9 =
4 + 4 +9 =  17 .
17 .
Тогда |
−1 2 +3 2 + (−3) (−3)≈ 0,72 ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
cos ϕ = |
ϕ ≈ 48,5o. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
19 |
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3) Уравнение |
плоскости, проходящей |
|
через |
три |
заданные точки |
||||||||||||||||||||||||||||||||||
A(x1, y1, z1 ) |
, B(x2 |
, y2 , z2 ) |
, |
|
|
C(x3 , y3 |
, z3 ), имеет вид: |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
(x − x1 ) |
(y − y1 ) |
|
|
|
|
|
|
|
(z − z1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
(x2 − x1 ) (y2 − y1 ) (z2 − z1 ) |
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
(x3 − x1 ) (y3 − y1 ) (z3 − z1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Подставляя значения координат, вычисляем определитель и |
|||||||||||||||||||||||||||||||||||||||
приравниваем его нулю: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x −3 y − 2 z − 4 |
|
|
|
|
x −3 y − 2 z − 4 |
|
= −15x − 4 y + z + 49 = 0 . |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
2 −3 5 − 2 1 − 4 |
|
= |
|
−1 |
3 |
−3 |
|
|
||||||||||||||||||||||||||||||
|
3 −3 1 − 2 0 − 4 |
|
|
|
|
|
|
|
0 |
|
|
|
−1 |
− 4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Итак, искомое уравнение плоскости имеет вид |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
−15x − 4 y + z + 49 = 0 или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
15x + 4 y − z − 49 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(x1, y1, z1 ) |
|
||||||||||||||||||||||
4) Уравнение |
|
прямой, проходящей |
через |
точки |
и |
||||||||||||||||||||||||||||||||||
D(x2 , y2 , z2 ), имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x − x1 |
|
= |
y − y1 |
= |
|
|
z − z1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x |
2 |
− x |
|
y |
2 |
− y |
|
|
|
z |
2 |
|
− z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, получаем искомое уравнение: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
x −3 |
= |
|
y − 2 |
= |
z − 4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
Ax + By +Cz + D = 0 |
|
|
|
|
|
||||||||||||||
5) Если |
|
дана |
|
|
плоскость |
|
|
с |
нормальным |
||||||||||||||||||||||||||||||
вектором |
|
|
N = {A, B,C} |
|
|
|
и |
прямая |
|
|
|
x − x0 |
|
= |
y − y0 |
= |
z − z0 |
|
с |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = {m, n, p}, |
|
|
|
|
m |
|
|
n |
|
|
|||||||
направляющим |
вектором |
|
|
то |
|
угол между прямой |
и |
||||||||||||||||||||||||||||||||
плоскостью определяется по формуле
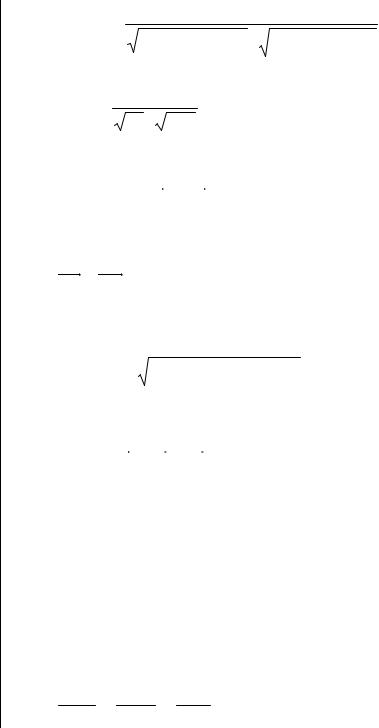
32
|
Am + Bn +Cp |
|
sin ϕ = ± |
A2 + B2 +C 2 |
m2 + n2 + p2 . |
Так как N = {15;4;−1}, а a = {2;2;−3}, то |
||
sin ϕ = 30 +8 +3 ≈ 0,64 , |
ϕ ≈ 44,2o. |
|
|
17 242 |
|
6) Площадь треугольника, построенного на двух векторах, равна половине модуля векторного произведения этих векторов:
S ABC |
= |
|
1 |
|
AB × AC |
|
. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как |
|
|
|
i |
j |
k |
|
|
|
|
|||||||||||||||
AB × AC = |
|
|
= −15i −4j +k , |
||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
−1 3 −3 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
−1 |
− 4 |
|
|
|
|
|||||||||||
то |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S ABC |
= |
|
|
|
(−15)2 +(−4)2 +12 ≈ 7,8 (кв. ед.). |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7) Объем пирамиды, построенной на трех векторах, равен одной |
|||||||||||||||||||||||||
шестой модуля смешанного произведения этих векторов: |
|||||||||||||||||||||||||
V = |
1 |
|
AB AC AD |
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
V = |
1 |
|
−1 |
3 |
−3 |
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
0 |
|
|
|
−1 |
− 4 |
|
= |
|
|
−3 − 24 −8 −6 |
|
≈ 6,8 (куб. ед.) |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
6 |
|
2 |
|
|
2 |
−3 |
|
|
6 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
8) Так как в качестве направляющего вектора прямой, проходящей через заданную точку D перпендикулярно плоскости ABC, можно выбрать вектор нормали N к плоскости, то каноническое уравнение искомой прямой запишется в виде
x −5 = y − 4 = z −1. 15 4 1
21.Длина стороны ромба с острым углом 60° равна 2. Диагонали ромба пересекаются в т. М(1;2), причем большая диагональ параллельна оси абсцисс. Составить уравнения сторон ромба. Сделать чертеж.
22.Даны координаты двух вершин треугольника А(-1;3), В(2;5) и точки пересечения его высот Н(1;4). Найти координаты третьей вершины треугольника и составить уравнения его сторон. Сделать чертеж.
23. Даны уравнения сторон треугольника: x + 2 y +1 = 0 , 2x − y −2 = 0 , 2x + y + 2 = 0 . Составить уравнение высоты, опущенной на третью сторону.

33
Сделать чертеж.
24. Точка А(1;2) является серединой одного из оснований прямоугольной трапеции, а точка В(3;-1) – серединой средней линии. Боковая сторона,
перпендикулярная |
основаниям, |
лежит на |
прямой |
x +1 |
= |
|
y −2 |
. Составить |
|
3 |
|
|
4 |
||||||
|
|
|
|
|
|
|
|||
уравнения остальных сторон трапеции. Сделать чертеж. |
|
|
|
|
|||||
25. Точка А(2;0) |
является |
вершиной |
правильного |
|
треугольника, а |
||||
противолежащая ей сторона лежит на прямой x + y −1 = 0 составить уравнения двух других сторон. Сделать чертеж.
26.Даны координаты двух вершин треугольника А(2;-1), В(1;5) и точки пересечения его биссектрис L(3;0). Составить уравнения сторон треугольника. Сделать чертеж.
27.Даны две вершины треугольника А(3;-1) и В(1;4) и точка пересечения его медиан L(0;2). Найти координаты третьей вершины треугольника и составить уравнения его сторон. Сделать чертеж.
28.Точки K(1;3) и L(-1;1) являются серединами оснований равнобедренной трапеции. Точка А(-5;5) является одной из вершин трапеции, а точка Q(-3;5) лежит на боковой стороне. Составить уравнения сторон трапеции. Сделать чертеж.
29.Точка Н(-3;2) является точкой пересечения высот треугольника, две стороны которого лежат на прямых y = 2x и y = −x +3 . Составить уравнение
третьей стороны. Сделать чертеж.
30. Гипотенуза прямоугольного треугольника лежит на прямой 2x + y − 2 = 0, а
точка С(3;-1) является вершиной прямого угла. Площадь треугольника равна 9 4 . Составить уравнения прямых, на которых лежат катеты. Сделать чертеж.
4 . Составить уравнения прямых, на которых лежат катеты. Сделать чертеж.
Литература к задачам 21-30: [1], гл.5, §1,2; [2], §11-23; [3], т.1, гл.I, §2; [6], гл. II, §2; [7], ч.1, гл. II, III; [9], с.15-61; [22], §2.3.
Пример. Точка А(3;4) является вершиной квадрата, а точка O(2;2) – точкой пересечения его диагоналей. Составить уравнения сторон квадрата.
Сделать чертеж. |
|
|
|
|
|
|
|
|
|
|
|
Воспользуемся тем свойством квадрата, |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
A |
|
|
|
|
|
что его диагонали пересекаются под прямым |
|
|
|
|
|
|
|
|
|||
углом, и при этом точка пересечения делит |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
диагонали пополам. |
|
|
|
|
|
|
|
|
|
|
|
Найдем сначала координаты вершины С |
|
|
|
|
|
|
|
|
|
|
|
квадрата, противоположной вершине А. Для |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
этого определим уравнение прямой, проходящей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|||
|
|
|
|
|
|
|
|
|
|||
через точки А и С и отложим на ней отрезок ОС, |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
равный АО. |
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||
Уравнение прямой, проходящей через две |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
точки, имеет вид |
|
|
|
|
|
|
|
|
|
|
|

34
x − xA |
= |
y − yA |
, следовательно, |
x −3 |
= |
y −4 |
, или |
|
xO − xA |
|
−1 |
|
−2 |
||||
|
yO − yA |
|
|
|||||
−2(x −3)= −1(y −4), |
|
|
|
|
|
|||
y = 2x −2 - уравнение прямой АО.
Так как АО=ОС, то xA − xC = xO − xC , yA − yC = yO − yC , xC = 2xO − xA =1, yC = 2 yO − yA = 0.
Итак, С(1;0).
Для определения вершин В и D проведем через т. О прямую, перпендикулярную АС, и отложим на ней отрезки, равные АО, в противоположные от т. О стороны.
Как известно, угловые коэффициенты взаимно перпендикулярных прямых связаны соотношением k1 = −1 k2 , следовательно, искомый
k2 , следовательно, искомый
угловой коэффициент k1 = −1 2 , а уравнение прямой ВО имеет вид
2 , а уравнение прямой ВО имеет вид
y = − 12 x +b .
Определим значение b, зная, что данная прямая проходит через точку O(2;2):
|
2 = − |
1 |
|
2 +b , следовательно, b = 3. |
|||||||
|
|
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|||
|
Таким образом, |
||||||||||
|
|
y = − |
1 |
x +3 - уравнение прямой АО. |
|||||||
|
|
||||||||||
|
|
|
|
|
|
2 |
|
||||
|
Отложив теперь от т. О на этой прямой отрезки длиной AO = 5 , |
||||||||||
получаем: |
|
|
|
|
|
||||||
|
|
|
|
(x − 2)2 +(y −2)2 = 5 , или, возведя обе части в квадрат, |
|||||||
|
|
x2 −4x + y2 − 4 y +3 = 0 . |
|||||||||
|
А |
|
так как координаты точек прямой связаны соотношением |
||||||||
y = − |
1 |
x +3 , то получаем |
|||||||||
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
5 |
x |
2 |
−5x = 0 , |
||||||
|
4 |
|
|||||||||
|
|
|
|
|
|
|
|
||||
xB = 4 , xD = 0, yB =1, yD = 3 .
Очевидно, эти две пары координат определяют вершины В(4;1) и
D(0;3).
Итак, найдены координаты всех вершин квадрата. Теперь несложно построить уравнения прямых, на которых лежат его стороны.
Прямая АВ:

35
|
x −3 |
= |
|
|
y −4 |
, или y +3x −13 = 0. |
||
1 |
|
|
−3 |
|||||
|
|
|
|
|
||||
Прямая ВС: |
|
|||||||
|
x − 4 |
= |
|
|
y −1 |
, или 3y − x +1 = 0 . |
||
|
−3 |
|
−1 |
|
||||
|
|
|
|
|
||||
Прямая СD: |
|
|||||||
|
x −1 |
= |
|
y −0 |
, или y +3x −3 = 0. |
|||
|
−1 |
|
|
3 |
|
|||
|
|
|
|
|
||||
Прямая АD: |
|
|||||||
|
x −3 |
= |
|
|
y − 4 |
, или 3y − x −3 = 0 . |
||
|
−3 |
|
|
−1 |
||||
|
|
|
|
|
||||
Замечание. Можно было использовать и любые другие соотношения, позволяющие найти решение задачи, - например, использовать то свойство, что диагонали наклонены к сторонам под углом 45°; или, найдя одно из уравнений сторон, остальные можно было бы построить, используя свойства параллельных и перпендикулярных прямых, и т. п.
31-40. Линия задана уравнением ρ = ρ(ϕ) в полярной системе координат. Требуется:
1)Построить линию по точкам, начиная от ϕ = 0 до ϕ = 2π и придавая ϕ значения через промежуток π 8 .
8 .
2)Найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.
3)По уравнению в декартовой прямоугольной системе координат определить, какая это линия.
31. |
ρ = |
1 |
|
. |
32. |
ρ = |
2 |
|
. |
|
|
|
||||
3 +3cos ϕ |
2 −cos ϕ |
|
|
|
||||||||||||
33. |
ρ = |
3 |
. |
|
|
|
34. |
ρ = |
4 |
. |
|
|
|
|||
1−cos ϕ |
|
|
|
3 + cos ϕ |
|
|
|
|||||||||
35. |
ρ = |
5 |
|
|
|
|
. |
36. |
ρ = |
|
6 |
|
|
|
. |
|
2(1+ cos ϕ) |
|
2 −3cos ϕ |
||||||||||||||
37. |
ρ = |
7 |
|
|
. |
38. |
ρ = |
8 |
|
|
|
|
. |
|||
3 − 4cos ϕ |
5 + 2cos ϕ |
|||||||||||||||
39. |
ρ = |
9 |
|
|
|
. |
40. |
ρ = |
10 |
|
|
. |
||||
4 −5cos ϕ |
3 −3cos ϕ |
|||||||||||||||
Литература к задачам 31-40: [2], §24-40; [4], т.1, гл.I, §10; [5], т.I, р.I, гл.I, §5,6; гл.VI, §2-5; [9], с.61-73; [21], гл.2, §5.

36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. ρ = |
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
4 + cos ϕ |
|
|
|
|
|
|
|
|
|
|
|
||||
|
Заполним таблицу значений ρ = ρ(ϕ). |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
|
ϕ |
0 |
|
|
π |
π |
3 |
π |
π |
5 |
π |
3 |
π |
7 |
π |
|
|
|
|
|
/8 |
/4 |
/8 |
/2 |
/8 |
/4 |
/8 |
||||
|
ρ |
0,4 |
|
|
0,41 |
0,42 |
0,46 |
0,5 |
0,55 |
0,61 |
0,65 |
||||
|
|
|
|
|
|
|
|
||||||||
|
π |
9π/8 |
|
5π/4 |
11π/8 |
3π/2 |
13π/8 |
7π/4 |
15π/8 |
2π |
|||||
|
0,66 |
0,65 |
|
|
0,61 |
0,55 |
0,5 |
0,46 |
0,42 |
0,41 |
0,4 |
||||
По полученным значениям строим кривую.
ϕ = π 2
2
ϕ = 3π 8
8
ϕ = π 4
4
ϕ = π 8
8
ϕ = 0; 2π
1 ρ
Теперь определим уравнение данной линии в декартовой системе координат. Так как полярные координаты связаны с декартовыми соотношениями
ρ = x2 + y2 , cos ϕ = |
x |
, |
|
+ y2 |
|||
x2 |
|
то, подставляя эти значения в исходное уравнение, получаем
x2 + y2 = |
|
2 |
|
, или 4 |
x2 + y2 + x = 2 , |
|
x |
|
|||
4 + |
|
|
|
||
x2 + y2 |
|
|
|
||

37
16(x2 + y2 )= (2 − x)2 , 15x2 + 4x +16 y2 = 4.
Выделим полный квадрат в левой части уравнения:
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
2 |
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
15 |
x |
|
|
|
+ 2 |
|
|
|
|
|
x + |
|
|
|
|
− |
|
|
|
|
+16 y |
|
= 4 , |
|||||||||||
|
|
|
15 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
15 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
2 = |
64 |
|
|
|
|
|
|
|
|
|
|
||||||||
15 x |
+ |
|
|
|
|
|
|
|
+16 y |
|
|
|
, |
|
|
|
|
|
|
|
|
|||||||||||||
15 |
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
15 |
|
+ |
|
|
|
|
|
|
|
=1. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
8 2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Получили уравнение эллипса с полуосями a = 8 15, b = 2 15 и |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
центром в точке |
− |
|
|
;0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
41-50. Доказать совместность системы линейных уравнений и решить ее двумя способами: 1) методом Крамера; 2) Методом Гаусса.
|
2x +3y −16z = −3, |
|
− 2x +5y −5z =12, |
|
41. |
x + 4 y + z =15, |
42. |
3x − y + 2z = −3, |
|
|
− x −3y +12z =1. |
|
x + 7 y −6z =15. |
|
|
2x −5y −6z = −9, |
|
7x − 2 y +5z = −4, |
|
43. |
2x + 2 y −3z = −7, |
44. |
x − y −6z = 21, |
|
|
3x − y + z =10. |
|
3x −5y +3z = 4. |
|
|
−5x −6 y + z = 7, |
|
− x + 2 y + z = 7, |
|
45. |
2x + y |
= −4, |
46. |
2x + 4 y + z =1, |
|
x +5y − z = 3. |
|
3x + y +3z = −18. |
|
|
3x − y + 2z = −1, |
|
x −5y + 7z = 20, |
|
47. |
x + 2 y +10z = 2, |
48. |
−3x + 4 y +3z = −1, |
|
|
4x − y −3z = 6. |
|
5x − y + 2z =10. |
|
|
− x +8y +5z =1, |
|
4x −11y + 2z = −1, |
|
49. |
2x +3y − z = 7, |
50. |
x − 2 y + z = −7, |
|
|
3x − 2 y −13z = −1. |
|
6x −9 y + 2z = 3. |
|

38
Литература к задачам 41-50: [3], т.1, гл.I, §5; [5], т.I, р.I, гл.II, §2,6; [6], гл.IV, §2; [8], гл.2, §4; [9], с.124-139; [12], §1.9,1.10; [21], гл.3, §3; [22], §1.3.
Пример.
2x −3y + z = 2;x + 5y − 4z = −5;
4x + y −3z = −4.
Метод Крамера рассматривался в примере к задачам № 1-10, поэтому перейдем к решению системы методом Гаусса.
Перепишем систему в следующем виде:
x + 5y − 4z = −5;2x −3y + z = 2;
4x + y −3z = −4.
Теперь будем приводить систему к треугольному виду, последовательно исключая неизвестные. Начнем с исключения, например, неизвестной х во втором и третьем уравнениях. Для этого сначала прибавим ко второму уравнению первое, умноженное на (− 2), и запишем полученное уравнение вместо второго, а к третьему – первое, умноженное на (− 4), и запишем результат на место третьего уравнения. Первое уравнение оставим в неизменном виде. Таким, образом, получаем следующую систему:
x + 5y − 4z = −5; |
|
|
−13y + 9z =12; |
|
|
|
−19 y +13z =16. |
|
|
Теперь, оставляя в неизменном виде первое и второе уравнения,
исключаем переменную y в третьем. Для этого к третьему уравнению, |
||
умноженному на 13, прибавляем второе, умноженное на |
(−19). |
|
Получаем: |
|
|
x |
+ 5y − 4z = −5; |
|
|
−13y + 9z =12; |
|
|
|
|
|
− 2z = −20. |
|
|
|
|
Из последнего уравнения сразу следует значение неизвестной z. Подставляя его во второе уравнение, получаем y, а из первого уравнения после этого находим x:
x =5;y = 6;
z =10.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39 |
51-60. Найти |
собственные |
значения и |
собственные |
векторы линейного |
|||||||||||||
преобразования, заданного в некотором базисе матрицей А. |
|||||||||||||||||
|
|
−1 4 |
0 |
|
|
|
|
0 |
|
2 |
|
0 |
|||||
51. |
A = |
−1 |
3 |
0 . |
|
|
52. |
A = |
−1 |
|
−3 |
|
0 . |
||||
|
|
|
3 2 |
2 |
|
|
|
|
|
|
2 |
|
4 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
−3 |
||||||
|
|
|
3 |
0 |
0 |
|
|
|
|
|
|
5 |
3 |
4 |
|
|
|
53. |
A = |
1 |
2 |
3 . |
|
|
54. |
A = |
1 |
3 |
2 |
. |
|||||
|
|
|
3 |
0 |
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||
|
|
4 −1 − 2 |
|
|
|
|
−1 4 |
|
8 |
||||||||
55. |
A = |
0 |
|
− 2 |
1 . |
|
|
56. |
A = |
4 |
|
−7 |
|
4 . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
4 |
|
|
|
|
|
0 − 4 3 |
|
|
|
|
|
|
|
−1 |
||||||
|
|
−1 5 |
0 |
|
|
|
|
−3 0 5 |
|||||||||
57. |
A = |
0 |
2 |
0 . |
|
|
58. |
A = |
2 |
|
4 |
4 . |
|||||
|
|
|
0 |
3 |
4 |
|
|
|
|
|
|
1 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
−1 3 3 |
|
|
|
|
0 2 9 |
|
|||||||||
59. |
A = |
0 |
|
− 2 |
0 . |
|
|
60. |
A = |
0 |
3 |
0 |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 1 0 |
|
|
||
|
|
|
− 2 3 4 |
|
|
|
|
|
|
|
|||||||
|
|
Литература к задачам 51-60: [3], т.1, гл.III, §3; [6], гл.XI, §1; [12], §1.12; |
|||||||||||||||
[21], гл.1, §4; [22], §1.4. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
5 |
−7 |
0 |
|
|
|
|
|
|
|
|
|
Пример. A = |
−3 |
1 |
0 . |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
12 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
Для определения собственных чисел λ матрицы А составим и |
|||||||||||||
|
|
решим характеристическое уравнение |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
5 −λ |
−7 |
|
0 |
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
−3 |
1−λ |
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
12 |
6 |
−3 −λ |
|
|
|
|
|
|
|
|
||
|
|
|
|
Раскрывая определитель по элементам третьего столбца, получим |
|||||||||||||
|
|
|
|
(5 −λ)(1−λ)(−3 −λ) |
−21(−3 −λ)= 0 . |
|
|
|
|
|
|||||||
|
|
|
|
Решая уравнение, находим λ1 = −3 , λ2 = −2 , λ3 = 8. |
|||||||||||||
|
|
|
|
Координаты собственных векторов, соответствующих найденным |
|||||||||||||
|
|
собственным числам, определим из системы уравнений |
|||||||||||||||
|
|
|
|
(5 −λ)x −7 y + 0 z = 0, |
|
|
|
|
|
|
|||||||
|
|
|
|
−3x + (1−λ)y + 0 z = 0, |
|
|
|
|
|
|
|||||||
|
|
|
|
12x + 6 y +(−3 −λ)z = 0. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

40
Подставляя в систему λ1 = −3 , получаем
8x1 −7 y1 + 0 z1 = 0,
−3x1 + 4 y1 + 0 z1 = 0,12x1 + 6 y1 + 0 z1 = 0.
Решая эту однородную систему, имеем x1 = 0, y1 = 0, z1 = t , t R .
Следовательно, первым собственным вектором преобразования А является
0 X1 = 0 .
t
Нормируя вектор X1, найдем соответствующий единичный вектор
i1 = X1 . X1
Так как X1 = t , то i1 = {0,0,1}.
Подставив в систему λ2 = −2 , найдем координаты второго собственного вектора:
7x1 −7 y1 + 0 z1 = 0,−3x1 +3y1 + 0 z1 = 0,12x1 + 6 y1 − z1 = 0.
Решение |
системы: |
x2 = t, y2 = t, z2 =18t , |
t R . |
Второй |
||
собственный вектор |
|
|
|
|||
|
|
t |
|
|
|
|
X |
|
|
|
|
|
|
2 |
= t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
18t |
|
|
|
|
Так как X2 = t  326 , то i2
326 , то i2
При λ3 = 8 получаем
−3x1 −7 y1 + 0 z1 = 0,−3x1 −7 y1 + 0 z1 = 0,
12x1 + 6 y1 −11z1 = 0.
Решение этой системы: собственный вектор
|
|
|
7t |
|
X |
|
|
|
|
3 |
= |
−3t . |
||
|
|
6t |
|
|
|
|
|
|
|
= |
X |
2 |
|
1 |
, |
1 |
, |
18 |
|
|
= |
326 |
326 |
326 |
. |
||||
|
X2 |
|
|
|
|
||||
x3 = 7t, y3 = −3t, z3 = 6t , t R . Третий
