Тема 5. Обобщающие статистические показатели.

1. Виды статистических показателей.

2. Абсолютные и относительные величины.

3. Средние величины.

1. Виды статистических показателей.

После сводки и группировки данных наблюдения переходят к следующему – третьему этапу статистического исследования. Он состоит в дальнейшей обработке статистических таблиц путем расчета статистических показателей.

Статистический показатель – это обобщающая характеристика явления или процесса. Он характеризует всю совокупность единиц наблюдения и используется для анализа совокупности в целом.

С помощью статистических показателей решается одна из основных задач статистики: определяется количественная сторона явления, объединенная с качественной стороной.

Количественная сторона явления определяет число и его измеритель, т.е. статистические показатели выражают: что, где, когда и каким образом подлежит измерению.

Классифицировать статистические показатели можно следующим образом:

1. В зависимости от способа расчета:

- первичные показатели (абсолютные величины);

- вторичные показатели (средние или относительные величины).

2. В зависимости от признака времени:

- интервальные (характеризуют явление за определенный период);

- моментные (характеризуют явление на определенный момент времени).

3. По способу выполнения своих функций:

- показатели, характеризующие объем явления;

- показатели, характеризующие его средний уровень;

- показатели, характеризующие интенсивность проявления;

- показатели, характеризующие структуру;

- показатели, характеризующие изменения во времени или пространстве.

В статистике используют несколько видов статистических показателей:

- абсолютные величины;

- относительные величины;

- средние величины.

2. Абсолютные и относительные величины.

Абсолютными величинами называют показатели, которые выражают размеры, объемы, уровни общественных явлений и процессов.

Абсолютные величины могут выражаться в натуральных, условно-натуральных, трудовых или стоимостных единицах измерения.

Натуральными называют абсолютные величины, которые характеризуют величину признака в физических измерителях (например, мера массы, объема, площади).

Стоимостные абсолютные величины используются для характеристики явлений и процессов в денежном выражении (например, объем товарооборота, валовой продукции).

Условно-натуральные необходимы для характеристики производства одноименной продукции, которая имеет специфические потребительские свойства и используются, когда какой-либо продукт имеет несколько разновидностей, а необходимо определить общий выпуск продукции (например, условные банки, условные пары обуви).

Для характеристики затрат труда на производство продукции используют трудовые единицы измерения: чел-час, чел-дни.

Абсолютные показатели характеризуют состояние явления на момент времени или за определенный период, однако по их величине нельзя судить о динамике, структуре и качественных особенностях явления. Для этого существуют относительные показатели.

Относительные показатели – это обобщающие количественные показатели, которые выражают соотношение сравниваемых абсолютных величин.

Т.е. относительная величина – результат деления (сравнения) двух абсолютных величин. В числителе дроби стоит величина, которую сравнивают, а в знаменателе – величина, с которой сравнивают (база сравнения). В данном случае база сравнения принята за единицу. Полученная относительная величина выражена в виде коэффициента, который показывает, во сколько раз сравниваемая абсолютная величина больше базисной. В случае если основание принимается за 100, относительная величина выражается в процентах (%), если за 1000 – в промилле (‰).

Различают такие виды относительных величин:

- динамики;

- выполнения плана;

- планового задания;

- структуры;

- координации;

- сравнения;

- интенсивности.

Относительные величины динамики характеризуют изменение какого-либо явления во времени, представляют собой отношение значений одной и той же абсолютной величины в разные периоды времени и определяется по формуле:

,

где Х1 – абсолютный показатель в отчетном или анализируемом периоде,

Х0 – абсолютный показатель в прошлом или базисном периоде.

Различают относительные величины динамики базисные и цепные.

Базисные определяются как отношение уровня показателя в отчетном периоде к уровню показателя в базисном периоде (базисным, как правило, считается первый период ряда динамики).

Цепные определяются как отношение уровня показателя в отчетном периоде к уровню показателя в предыдущем периоде.

Относительные величины выполнения плана характеризуют степень выполнения плана, рассчитываются как отношение фактического показателя к плановому:

где Хп – плановый уровень показателя.

Относительные величины планового задания характеризуют изменения плана по сравнению с достигнутым уровнем за прошлый период:

.

Существует определенная связь между относительными величинами динамики, выполнения плана, планового задания:

.

Относительные величины структуры характеризуют состав совокупности, определяются как отношение части совокупности к общему итогу:

.

Относительная величина координации характеризует отношение какой-либо части объекта к другой его части, принятой за основу (базу сравнения) и определяется по формуле:

.

Относительная величина сравнения - это сравнение (соотношение) разных объектов по одинаковым признакам:

,

где А, Б – сравниваемые объекты.

Относительная величина интенсивности – это соотношение разных признаков одного объекта между собой:

,

где X – один признак объекта; Y – другой признак этого же объекта.

3. Средние величины.

Средняя величина в статистике – это обобщающая характеристика количественно и качественно однородной совокупности в определенных условиях. Среднее определяется по какому-либо признаку и проявляется в результате действия закона больших чисел, когда в массовых совокупностях индивидуальные отклонения от типичного уровня взаимопогашаются. Т.е. среднее позволяет заменить множество значений показателей одним типичным, что значительно упрощает последующий анализ явлений.

Средняя применяется в статистических исследованиях для оценки сложившегося уровня явления, для сравнения между собой нескольких совокупностей по одному и тому же признаку, для исследования динамики развития изучаемого явления во времени, для изучения взаимосвязей явлений.

Главное значение средних величин состоит в их обобщающей функции, то есть замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений.

Виды средних величин различаются прежде всего тем, какое свойство, какой параметр исходной варьирующей массы индивидуальных значений признака должен быть сохранен неизменным.

Выделяют следующие виды средних величин:

1. Средняя арифметическая.

2. Средняя гармоническая.

3. Средняя квадратическая.

4. Средняя геометрическая.

5. Средняя хронологическая.

Для несгруппированных данных используют средние простые, для сгруппированных (которые представлены в виде рядов распределения) – средние взвешенные.

1. Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Иначе можно сказать, что средняя арифметическая величина – среднее слагаемое. При ее вычислении общий объем признака распределяется поровну между всеми единицами совокупности.

Таким образом, средняя арифметическая простая рассчитывается как сумма отдельных значений признака X, деленная на число этих значений N:

.

Если изучаемая совокупность велика, исходная информация чаще представляет собой ряд распределения или группировку, при этом используется формула средней арифметической взвешенной:

,

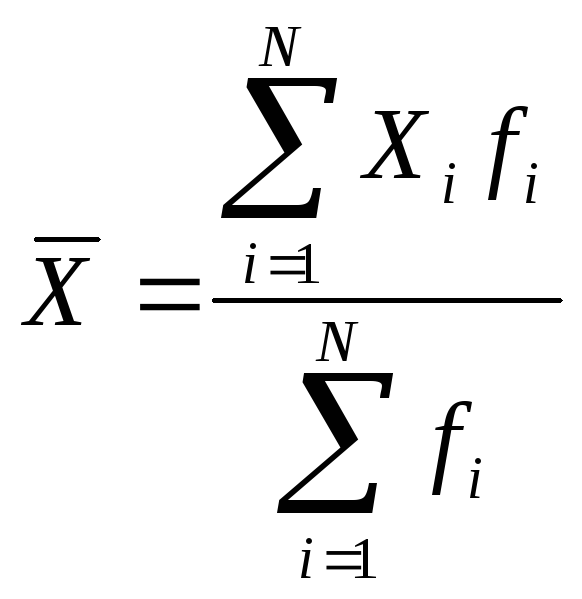где X_i - значения признака в каждой группе (варианта);

f_i - повторяемость признака (частота);

i – число групп.

Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, то есть исходят из предположения о равномерном распределении единиц совокупности по интервалу значений признака.

2. Средняя гармоническая взвешенная применяется когда статистическая информация не содержит частот f по отдельным вариантам X_i совокупности, а представлена как их произведение Xf. Для получения формулы обозначим Xf=w, откуда f=w/X:

.

В тех случаях, когда вес каждого варианта w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:

.

3. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменную сумму квадратов исходных величин, то средняя будет являться средней квадратической величиной. Формула средней квадратической простой имеет вид:

.

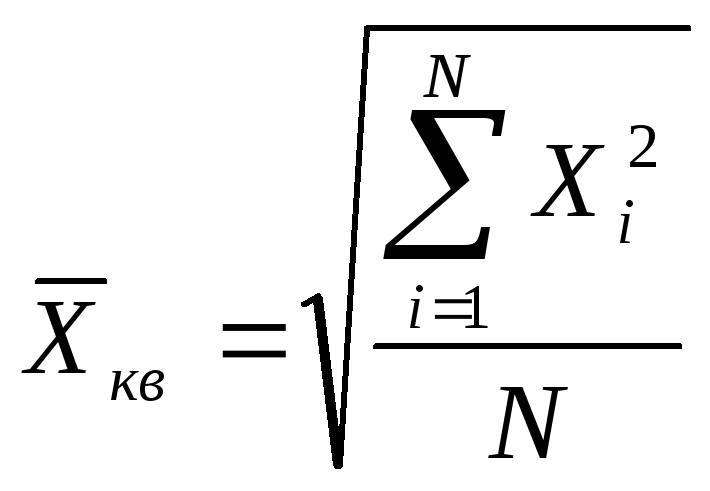Средняя квадратичная используется, когда значения признака представлены в виде отклонений от нормы или стандарта.

Формула средней квадратической взвешенной:

.

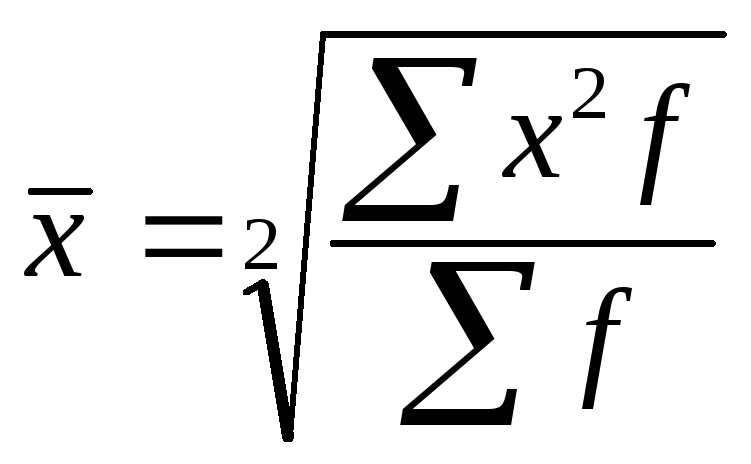Главной сферой применения квадратической средней является измерение вариации признака в совокупности.

4. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить среднюю геометрическую величину. Средняя геометрическая простая имеет следующий вид:

.

Основное применение средняя геометрическая находит при определении средних относительных изменений. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения признака, который качественно был бы равноудален как от максимального, так и от минимального значения признака.

5. Средняя хронологическая используется преимущественно в бухгалтерском учете для определения среднегодовых остатков материальных ценностей.

Все рассмотренные выше виды средних величин принадлежат к общему типу степенных средних, имеющему следующий вид:

=.

При m = 1 получаем среднюю арифметическую; при m = 2 – среднюю квадратическую; при m = 0 – среднюю геометрическую; при m = –1 – среднюю гармоническую. Чем выше показатель степени m, тем больше значение средней величины (если индивидуальные значения признака варьируют). Это называется правилом мажорантности средней.