
КТМ_Маслєєва та ін_Динаміка_точки
.pdf
|
|
|
|
|
mV1x |
mV0x |
t1 |
Fxdt |
||
|
|
|
|
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
Ця теорема зв’язує масу точки m , |
її швидкість V , сили Fi , що діють на |
|||||||||
точку в |
процесі руху, та час |
t . Теорему |
можна використовувати, коли |
|||||||
Fi const або Fi |
Fi (t) , тобто коли сили сталі або залежать від часу, що ви- |
|||||||||
пливає із вигляду інтегралу в правій частині виразу теореми. |
||||||||||
Теорема про зміну кінетичної енергії точки має вигляд: |
||||||||||
|
mV 2 |
|
mV 2 |
|
|
|
|
|
|
|
|
1 |
|
0 |
|
A0 1, де |
A0 |
1 – алгебраїчна сума робіт усіх сил, що ді- |
|||
2 |
2 |
|
||||||||
|
|
|
|
|
|
|
||||
ють на точку на заданому переміщенні із положення “0” в положення “1”. |
||||||||||
Робота сили в загальному випадку обчислюється за формулою: |
||||||||||
|
|
|
|
|
A |
|
|
S1 F cos |
dS, |
|
|
|
|
|
|
F |
|||||
|
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
де F – модуль (величина) сили, S – переміщення точки прикладання си- |
||||||||||
ли, – кут між напрямком сили і напрямком переміщення. |
||||||||||
Тоді |
можна |
вважати, що |
теорема |
про |
зміну кінетичної енергії точки |
|||||
зв’язує масу точки m , її швидкість V , сили Fi та переміщення точки S . Із
вигляду інтеграла роботи випливає, що теорему можна використовувати тільки тоді, коли сили, що діють на точку в процесі руху, сталі або залежать
від переміщення точки Fi |
|
const або Fi |
Fi S . |
|
|
|
|||||||||||
Приклад 1. Вказати правильну відповідь. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
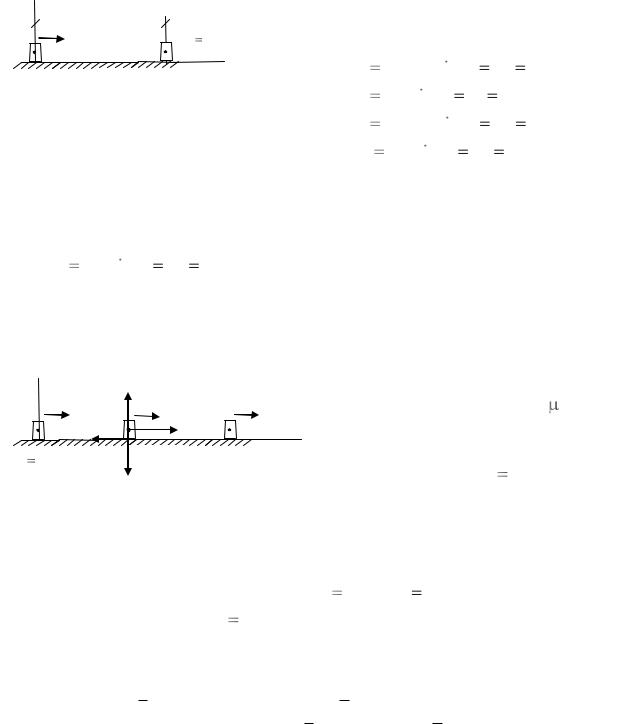
Якщо вагонетка |
(рис.7) вагою P котиться |
||||
FОП |
|
N |
|
|
|
||||||||||||
|
|
униз по площині, нахиленій під кутом α до гори- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
зонту, |
та сила загального опору руху дорівнює |
||||||
|
|
|
|
|
|
V |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
α |
|
|
|
|
|
|
|
Fоп , то диференціальне рівняння руху вагонетки |
|||||||
|
|
|
|
|
α |
|
(як точки) вздовж осі |
x має вигляд: |
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
P |
|
1) |
m x |
P cos |
Fоп ; |
|||||||||
|
|
|
|
|
|
|
|
|
x |
||||||||
|
|
Рис. 7 |
|
|
|
|
|
|
2) |
m x |
P Fоп sin ; |
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
3) |
m x |
P sin |
Fоп ; |
||||
|
|
|
|
|
|
|
|
|
|
4) |
m x |
P sin |
Fоп . |
||||
Розв’язання. Із умови прикладу випливає, що на вагонетку в процесі руху діє сила ваги P , реакція опорної площини N та сила опору руху Fоп . Тоді рух вагонетки як точки вздовж осі x описується наступним рівнянням дина-
міки (в проекції на вісь x ): max |
Fx , де сума проекцій на вісь x усіх сил, |
||||||
що діють на точку в процесі руху, становить |
Fx Psin |
Fоп. Якщо в рів- |
|||||
нянні динаміки проекцію прискорення вагонетки на вісь |
x замінити похід- |
||||||
ною від закону руху (ax |
a |
d 2 x |
|
x), то це рівняння стає диференціальним |
|||
dt2 |
|||||||
|
|
|
|
|
|||
відносно вказаної координати x : mx |
Psin |
Fоп. |
|
||||
11
Отже, правильною буде відповідь 4).
Приклад 2. Вказати правильну відповідь.
y |
|
|
|
|
|
Якщо тіло (рис. 8) масою m внаслідок по- |
|||
|
|
|
|
|
штовху отримало горизонтальну швидкість 4 м/с |
||||
|
|
|
|
S1 |
|
||||
|
|
|
|
|
та пройшло за 5 с відстань 24 м і зупинилось, то |
||||
|
|
|
|
|
|
|
|
|
|
|
V0 |
|
V1 |
0 |
початкові умови руху мають вигляд: |
||||
|
|
|
|
|
|
|
|
|
|
“0” |
x |
1) |
x 0 24 м; x 0 |
V0 |
0 ; |
|
“1” |
2) |
x 0 |
0; x 0 V1 |
0 ; |
|
|
|
Рис. 8 |
|
||||
|
3) |
x 0 |
24 м; x 0 |
V0 |
4 м/с ; |
|
|
|
|||||
|
|
4) x 0 0; x 0 V0 |
4 м/с. |
|||
Розв’язання. Початкові умови руху визначаються у початковий момент часу t = 0. Із умови прикладу випливає, що у цей час тіло отримало швидкість 4 м/с і почало рухатись із початку координат в заданій системі координат; тоді початкові умови руху мають вигляд:
x 0 0; x 0 V0 |
4 м/с. |
|
|
|
|
|||||||||||||||
Отже, правильною буде відповідь 4). |
|
|
|
|
||||||||||||||||
Приклад 3. |
Вказати правильну відповідь. Прискорення вільного падіння g |
|||||||||||||||||||
прийняти рівним 10 м/с2. |
|
|
|
|
|
|
|
|||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Якщо тіло масою m=10 кг починає |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рухатись по шорсткій горизонтальній |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
||||||
V0 |
|
|
|
|
|
|
|
|
V1 |
площині (коефіцієнт тертя |
=0,15) з |
|||||||||
|
|
|
|
|
|
|
V |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
початкової швидкістю |
V0 =4 |
м/с під |
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
дією сталої горизонтальної сили тяги |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(t 0) |
FTEPT |
|
( t ) |
|
|
|||||||||||||||
|
( t1 ) |
|||||||||||||||||||
|
|
|
|
|
|
T = 20 H, то через |
t |
5с від початку |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
P |
|
|
|
руху швидкість V1 набуває значення: |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Рис. 9 |
|
|
|
1) V1 = 6,4 м/с; |
2) V1 = 8,4 м/с; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) V1 = 4,2 м/с; |
4) |
V1 = 6,5 м/с. |
|
Розв’язання. Розглянемо рух тіла по шорсткій горизонтальній площині із початкового положення зі швидкістю V0 4 м/с t 0 в кінцеве положення, яке воно проходить через t1 5 c від початку руху з шуканою швидкістю V1 .
Зобразимо вказані положення на рис. 9; покажемо також на рисунку проміжне положення тіла між початковим і кінцевим в довільний момент часу t і зобразимо в цьому положенні сили, що діють на тіло в процесі руху: крім заданої сили тяги T на тіло діє сила ваги P і реакція шорсткої площини, що складається із нормальної складової N і сили тертя FТЕРТ . Усі ці сили відомі
(їх можна визначити за умовою прикладу), а треба знайти кінематичну характеристику руху тіла – швидкість V1 . Оскільки тіло рухається поступально, то
далі його будемо розглядати як точку. Тоді із умови прикладу випливає, що поставлене питання відноситься до другої задачі динаміки точки.
12

Цю задачу, як відомо, можна розв’язати шляхом інтегрування диференціального рівняння руху точки (універсальний спосіб) і за допомогою однієї із загальних теорем динаміки точки, так як в даному випадку сили, що діють на точку в процесі руху, сталі. Розв’яжемо цей приклад двома вказаними способами.
Перший спосіб. Складемо диференціальне рівняння руху точки і проінтегруємо його, склавши початкові умови задачі. Для цього рівняння динаміки
|
|
|
|
|
|
точки у векторній |
формі ma |
F спроектуємо на координатні осі x, y |
|||
(рис.9) і представимо в диференціальному вигляді: |
|||||
|
|
mx |
Fx ; |
||
|
|
my |
Fy. |
||
Врахуємо, що x |
ax a; y |
ay |
0. |
||
Тоді попередні рівняння приймають вигляд: |
|||||
|
|
mx |
Fx ; |
||
|
|
0 |
|
|
Fy. |
Тобто перше рівняння залишається рівнянням динаміки точки, що описує її рух вздовж осі x , а друге рівняння перетворюється в рівняння статики (точка вздовж осі y не переміщується) і його будемо використовувати як допо-
міжне – для обчислення сили тертя |
FТЕРТ . Оскільки сила тертя виражається |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
через нормальну реакцію площини |
N |
(FТЕРТ |
N |
), то цю силу N треба |
||||||||||||||
знайти. Визначимо її з рівняння рівноваги: |
Fy |
0 . Вказане рівняння рівно- |
||||||||||||||||
ваги для даного випадку має вигляд: |
N |
P |
0, |
звідки N P |
mg const. |
|||||||||||||
Тоді FТЕРТ |
mg |
|
const. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Диференціальне рівняння руху тіла (як точки) вздовж осі x |
приймає ви- |
|||||||||||||||||
гляд mx |
F |
FТЕРТ , тобто mx |
|
F mg |
; рівняння можна спростити, розді- |
|||||||||||||
ливши на m : x |
|
F |
g |
. Зауважимо, що права частина цього рівняння ста- |
||||||||||||||
|
|
|||||||||||||||||
|
m |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ла і x Vx |
V ; |
тоді x |
Vx |
V |
|
dV |
|
і диференціальне рівняння зі сталою |
||||||||||
|
|
|
|
|||||||||||||||
|
dt |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
правою частиною приймає вигляд: |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
dV |
|
F |
g . |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
dt |
|
m |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Оскільки в прикладі треба визначити швидкість тіла в заданий момент часу, то останнє рівняння і треба проінтегрувати при належних початкових умовах задачі: при t = 0 Vx 0 x 0 x0 V0 4 м/с.
Для цього розділимо змінні і знайдемо перший інтеграл диференціального рівняння – закон зміни за часом швидкості тіла V V t :
13

dV |
|
F |
g dt; |
dV |
F |
|
g dt; |
||||
|
|
|
|
|
|||||||
|
m |
m |
|||||||||
|
|
|
|
|
|
|
|
|
|||
|
dV |
|
F |
g |
dt; V |
|
|
F |
g t C1, |
||
|
|
|
|
|
|
||||||
|
|
m |
|
|
m |
||||||
|
|
|
|
|
|
|
|
|
|
||
де C1 – стала інтегрування, що визначається із початкової умови задачі.
П р и м і т к а. Оскільки множник F |
g |
під знаком інтегралу є величина стала, то |
|
|
m |
|
|
|
|
|
|
він був винесений із-під знаку інтеграла.
Знайдемо сталу інтегрування C1 :
|
при t |
0 |
V0 |
F |
g 0 C1; |
С1 V0 |
4 м/с. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
m |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Тоді закон зміни швидкості за часом приймає вигляд V |
|
F |
g |
t |
V0 ; |
|||||||||||||
|
|
|
|
||||||||||||||||
|
|
m |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
значення |
|
швидкості |
тіла |
V1 |
при |
t1 |
5 c |
буде |
|
таким: |
|||||||||
V1 |
|
F |
g |
t V0 |
20 |
10 0,15 |
5 4 |
2 1,5 5 |
4 |
0,5 5 4 |
2,5 |
4 6,5 м/с. |
|||||||
|
|
|
|
|
|
||||||||||||||
|
m |
10 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Отже, правильною буде відповідь 4).
Другий спосіб. Спробуємо відповісти на питання прикладу за допомогою однієї із загальних теорем динаміки точки. Оскільки треба визначити швидкість точки в заданий момент часу, то тут необхідно використовувати інтегральну форму теореми про зміну кількості руху точки (в проекціях на вісь x), бо вона зв’язує масу точки, її швидкість V , сили, що діють на точку, і час t :
|
|
t1 |
|
mV1x |
mVox |
Fxdt. |
|
|
|
0 |
|
Тут (див. рис.9) V1x V1, V0x |
V0, |
Fx F Fтерт F mg |
const. |
Підставивши у вираз теореми вказані величини, отримаємо:
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
mV1 |
mV0 |
F |
mg |
|
|
|
dt; |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
mV1 |
mV0 |
(F |
mg |
) |
|
dt; |
||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
mV1 |
mV0 |
(F |
mg |
) |
t |
|
t1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
0 ; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mV1 |
mV0 |
(F mg ) t1; |
||||||
V1 V0 |
F |
g |
t1 |
4 |
20 |
10 0,15 |
5 4 |
|
|
2 1,5 5 4 2,5 6,5 м/с. |
|||
|
|
|
|
|
|||||||||
m |
10 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Отже, правильною буде відповідь 4).
14

Приклад 4. Вказати вірну відповідь. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
На заданому переміщенні SA |
(рис. |
10) |
||||||||||
|
|
|
SA |
|
|
|
|
|
від’ємну роботу |
A |
|
|
0 виконує: |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1) сила Q ; |
2) |
сила N ; 3) |
сила P . |
|||||||||
Q |
A |
|
N |
|
|||||||||||||||||
|
|
Розв’язання. В даному прикладі розг- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
лядається рух тіла А уверх по нахиленій |
||||||||||||
|
|
α |
|
|
|
V |
|
||||||||||||||
|
|
|
|
|
|
|
|
площині, що розташована під кутом |
до |
||||||||||||
|
|
|
β |
|
|
|
|
|
горизонту. Треба визначити, яка з трьох |
||||||||||||
Рис. 10 |
|
P |
β |
||||||||||||||||||
|
сил, що діє на тіло під час руху, виконує |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
від’ємну роботу на переміщенні тіла SA. |
||||||||||||
П р и м і т к а. Робота сили характеризує ефект дії сили на тіло (точку) на заданому переміщенні тіла (точки).
Щоб відповісти на питання прикладу, треба скористуватися формулою для обчислення роботи сили, яка має вигляд
|
S 1 |
AF |
F cos dS . |
|
0 |
Тут F − модуль (величина) сили, S − переміщення точки прикладення си- |
|
ли, − кут між напрямком сили і напрямком переміщення. Із формули ви- |
|
пливає, що знак роботи дає множник cos . Якщо кут гострий ( |
90 ), то |
значення косинуса додатне і робота сили додатна (+); якщо кут |
α тупий |
( |
90 ), то значення косинуса від’ємне і робота сили від’ємна (–); якщо кут |
||
|
|
прямий (α = 90°; сила перпендикулярна до переміщення), то значення ко- |
|
синуса дорівнює нулю і робота сили дорівнює нулю. |
|||
|
|
В даному випадку тупий кут з напрямком переміщення SA утворює сила |
|
P |
90 |
. Оскільки косинус тупого кута від’ємний, тому від’ємну ро- |
|
боту буде виконувати сила P .
Отже, правильною буде відповідь 3).
П р и м і т к а. Із інтегральної формули для обчислення роботи сили випливає така ознака, що допомагає визначити без розрахунків знак роботи: якщо сила прискорює рух точки (тіла), то робота її додатна(+); якщо уповільнює рух – то робота її від’ємна (–); якщо
жсила не впливає на рух (не прискорює його і не уповільнює), то робота її дорівнює нулю.
Вданому прикладі прискорює рух тіла А сила Q , бо спрямована вона у бік руху
|
|
|
|
|
|
|
|
|
|
( |
0, cos |
1) і робота її додатна; уповільнює рух тіла сила |
P (вона гальмує рух тіла |
||||||
|
|
|
|
|
|||||
уверх по площині) і робота її від’ємна; не впливає на рух тіла сила N (не прискорює рух і |
|||||||||
|
|
|
|
|
|
||||
не уповільнює його), тому робота її дорівнює нулю ( |
90 , cos |
|
0); сила N перпендику- |
||||||
лярна до переміщення SA. |
|
|
|
|
|
|
|
||
Приклад 5. Вказати правильну відповідь. Прискорення вільного падіння g
прийняти рівним 10м/с2. Обчислення проводити з точністю до трьох значущих цифр.
15

y |
Якщо тіло А масою m=100 кг спускається |
|
по негладкий площині, що розташована під |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кутом |
30 |
до горизонту, а коефіцієнт тертя |
|||
|
|
|
|
|
|
|
|
|
|
SA |
=0,1; то робота сили тертя на переміщенні |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тіла SА=10 м становить: |
|
||||
|
|
|
|
|
|
N |
|
|
|
|
|
|
||||||||
|
|
|
|
A |
|
|
|
|
|
|
|
1) |
AF |
терт |
866 H м; |
|||||
|
|
|
|
|
|
|
|
|
|
V |
|
|
2) |
AF |
|
893 H м; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F |
|
|
|
|
|
|
|
|
||||||||||||
|
TEPT |
|
|
|
|
|
|
|
|
терт |
|
|||||||||
300 |
|
|
|
|
|
|
|
|
|
|
|
3) |
AF |
|
456 H м; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
терт |
|
|
|
|
|
|
|
|
|
P |
300 |
|
|
|
|
4) |
AF |
|
566 H м. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
терт |
|
|
Рис. 11 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Розв'язання. Розглянемо рух тіла А по |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шорсткій похилій площині під дією сили |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ваги P і реакції площини, |
що складається із двох складових: нормальної |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
складової N і сили тертя F |
, що спрямована у бік, протилежний руху. По- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ТЕРТ |
|
|
|
|
|
||
кажемо ці сили на рис.11 |
|
|
|
|
|
|
||||||||||||||
|
Сила тертя обчислюється за формулою: |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FТЕРТ |
N |
, |
|
|
|
де N  нормальна реакція поверхні.
нормальна реакція поверхні.
Для визначення сили N складемо рівняння рівноваги тіла відносно осі y ,
що перпендикулярна до площини, оскільки рух тіла вздовж цієї осі не відбувається:
Fy |
0; |
N P cos30 0 |
N |
P cos30 |
mg cos30 . |
Тоді FТЕРТ mg cos30 |
і є сталою величиною. |
|
Роботу сталої сили можна розрахувати за спрощеним правилом: вона дорівнює добутку модуля сили на переміщення точки прикладення сили і на косинус кута між напрямком сили і напрямком переміщення. Кут між напря-
мком сили тертя і напрямком переміщення дорівнює 180 . Тоді
AF |
ТЕРТ |
FТЕРТ S А cos180 |
FТЕРТ S А 1 |
mg cos30 |
S А |
100 10 0,866 0,1 10 |
866 H м. |
|
|
||
Отже, правильною буде відповідь 1).
Приклад 6. Вказати правильну відповідь. Прискорення вільного падіння g прийняти рівним 10 м/с2.
Якщо тіло масою m піднімається з початковою швидкістю V0 по гладкій нахи-
леній площині, що розташована під кутом |
30 до горизонту та шлях, пройде- |
ний тілом до зупинки (V1 0), дорівнює S1 |
4 м, то значення цієї початкової |
швидкості становить: |
|
16

|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) V0 |
1,22 м/с; |
2) V0 |
3,15 м/с; |
||||
|
|
|
S1 |
|
|
|
|
|
|
|
|
|
3) V |
4,24 м/с; |
4) V |
6,32 м/с. |
|||||
|
|
|
|
|
|
|
|
|
|
V1 |
0 |
0 |
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
Розв'язання. В даному прикладі можна |
|||||||||||
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
V |
|
вважати, що сили, які діють на тіло, відомі |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
“1” |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
і вони сталі. Це сила ваги P і реакція глад- |
|||||||||||||||
|
V0 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кої площини N . Покажемо ці сили на рис. |
|||||||
|
“0” |
|
|
|
300 |
|
|
|
|
12. Оскільки тіло рухається поступально, |
|||||||||||
300 |
|
P |
|
|
|
|
то далі будемо розглядати його як точку, |
||||||||||||||
Рис. 12 |
|
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
початкову швидкість |
якої (V0 ) треба ви- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
значити. Це друга задача динаміки точки: сили відомі, визначити кінематичну характеристику руху точки.
Тому на питання прикладу можна відповісти за допомогою теореми про зміну кінетичної енергії точки, бо теорема зв’язує масу точки m , швидкість точки V , сили, що діють на точку, і переміщення точки, яке в даному прикладі задано ( S1 4 м).
Записуємо вираз теореми, враховуючи, що точка переміщується із положення “0” в положення “1”:
|
|
|
mV 2 |
|
mV 2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
|
|
0 |
|
|
|
A0 1 , |
|||||
2 |
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
де A0 1 – це сума робіт усіх сил, що діють на точку на заданому перемі- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
щенні, яка складається із роботи двох сил – |
N і P : |
||||||||||||||||
|
|
|
|
A0 1 |
A |
|
|
A |
|
|
|
|
|||||
|
|
|
N |
P |
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Оскільки сила N стала, але перпендикулярна до переміщення, то вона |
|||||||||||||||||
роботу не виконує: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
AN |
|
N S1 |
cos90 0. |
||||||||||||
Роботу сили ваги P теж можна розписати як роботу сталої сили, бо вона стала за величиною і стала за напрямком по відношенню до переміщення; кут
між напрямком сили P і напрямком переміщення становить Тоді
A |
|
|
P S1 |
cos120 mg S1 cos120 |
mg S1 0,5. |
||
P |
|||||||
Таким чином |
A0 1 |
0 mg S1 |
0,5. |
|
|||
Підставимо значення величин в теорему |
|
||||||
|
|
|
|
|
mV 2 |
|
|
|
|
|
|
0 |
0 |
mg S1 0,5 |
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
і отримаємо значення шуканої початкової швидкості тіла
V0 
 2g S1 0,5
2g S1 0,5 
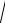 2 10 4 0,5
2 10 4 0,5 
 40 6,32 м/с.
40 6,32 м/с.
Отже, правильною буде відповідь 4).
Приклад 7. Вказати правильну відповідь.
17

Якщо тіло (рис.13) масою m піднімається без початкової швидкості (V0 0) по гладкій похилій площині, що складає кут α
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
з горизонтом, під дією сили тяги T , то за |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
теоремою про зміну кількості руху матері- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
N |
V |
|
|
|
|
|
альної точки на відрізку часу 0 ÷ t1 маємо: |
||||||||||||
|
|
|
Т |
|
( t1 ) |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
mV1 |
T |
P sin |
t1 ; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
V0 |
0 |
|
|
|
|
|
( t ) |
|
|
|
|
2) |
mV0 |
T |
P sin |
t1 ; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
(t |
0) |
|
|
α |
|
|
|
|
|
|
3) |
mV1 |
T |
P cos |
t1 ; |
|||||
α |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
mV0 |
T sin |
P t1 . |
||||
|
|
|
|
|
|
P |
|
|
|
|
Рис. 13 |
|
||||||||||
Розв'язання. Оскільки тіло рухається поступально, то далі його будемо розглядати як точку.
Із умови прикладу випливає, що для отримання відповіді треба скористатися теоремою про зміну кількості руху точки в інтегральній формі в проек-
|
t1 |
ціях на вісь x , що спрямована в напрямку руху: mV1x mV0x |
Fxdt, де |
|
0 |
Fx – сума проекцій на вісь x сил, що діють на точку в процесі руху. Зобразимо ці сили (в довільний момент часу t ) на рис.13; тоді проекція швидкості
на вісь x в початковий момент часу дорівнює нулю – V0x |
0, оскільки за |
|
умовою прикладу тіло рухалось без початкової швидкості (V0 |
0); швидкість |
|
точки в кінцевий момент часу t1 |
проектується на вісь x в натуральну вели- |
|
чину зі знаком плюс – V1x V1, а |
Fx T Psin . |
|
Після підстановки вказаних величин в теорему її вираз приймає вигляд:
t1
mV1 0 T P sin dt.
0
Враховуючи той факт, що під знаком інтегралу стоять сталі величини – T , P, , то отримуємо такий результат:
t1
mV1 T P sin dt;
0
mV |
T |
Psin |
t |
|
t1 ; |
|
|||||
1 |
|
|
|
|
0 |
|
|
|
|
|
|
mV1 |
T |
Psin |
t1 . |
||
Отже, правильною буде відповідь 1).
Приклад 8. Вказати правильну відповідь. Обчислення проводити з точністю до трьох значущих цифр.
Якщо тіло рухалось по горизонтальній площині під дією горизонтальної сили
F 2t2 (Н), то проекція імпульсу цієї сили на горизонтальну вісь x, що спрямована у напрямку дії сили, за проміжок часу 0 2 с дорівнює:
18
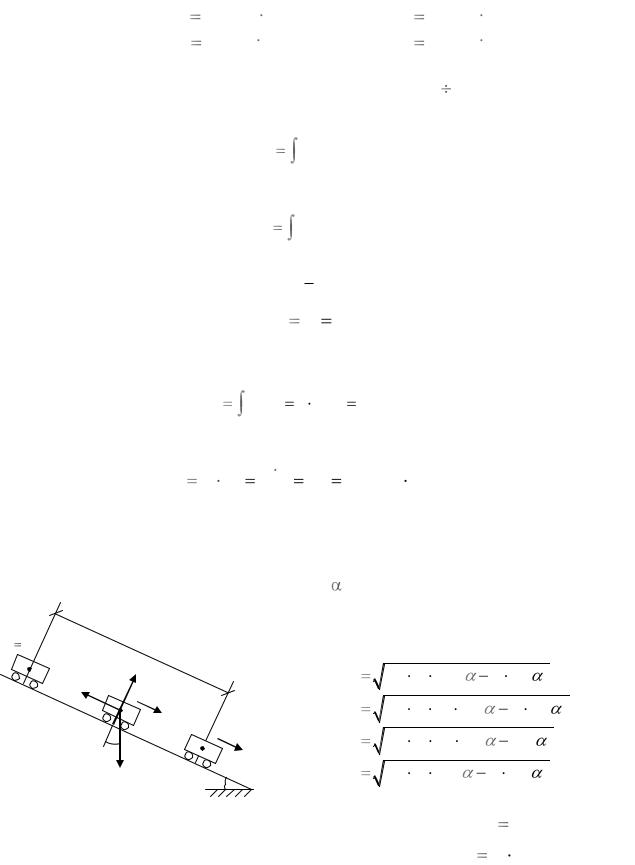
1) |
Lx |
5,33 H c; |
2) |
Lx |
8,33 H c; |
3) |
Lx |
15,8 H c; |
4) |
Lx |
21,4 H c. |
Розв'язання. Імпульс сили – це векторна величина, яка характеризує ефект дії сили на тіло (точку) за деякий проміжок часу 0 t1 і визначається за
векторною формулою:
|
|
t1 |
|
|
L |
Fdt. |
|||
|
|
0 |
|
|
В проекції на вісь x ця формула приймає скалярний вигляд: |
||||
|
|
t1 |
||
Lx |
Fx dt, |
|||
|
|
0 |
|
|
де Lx – проекція імпульса сили на вісь x , Fx – проекція вектора сили на вісь x . В даному випадку вектор сили F проектується на вісь x в натураль-
ну величину зі знаком плюс, тобто F |
F |
|
2t2 . |
|||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
Тоді вираз для обчислення |
проекції імпульсу заданої сили на вісь x |
|||||||||||||||
приймає вигляд: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lx |
t1 |
2t |
2 |
dt 2 |
|
|
t3 |
|
t |
2 3 |
|||||
|
|
|
|
|||||||||||||
|
|
|
3 |
|
|
0 |
|
3 t1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
і значення Lx становить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Lx |
2 |
|
23 |
|
2 8 |
|
16 |
|
|
|
5,33 Н с . |
|||||
3 |
|
|
|
3 |
|
|
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Отже, правильною буде відповідь 1).
Приклад 9 Вказати правильну відповідь.
Якщо вагонетка (рис.14) рухається без початкової швидкості самокатом униз
по похилій площині, розташованій під кутом |
до горизонту, |
і коефіцієнт опору |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
руху дорівнює f, то на заданому переміщенні |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
S1 |
|
|
S1 |
вона набуває швидкість V1 , яка обчислю- |
|||||||||||||||
V0 0 |
|
|
|
|
|
|
ється за формулою: |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
1) |
V1 |
2 g S1 |
cos |
|
f |
sin |
; |
|
||||||||
|
|
FОП |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
“0” |
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2) |
V1 |
2 g S1 |
f |
cos |
|
|
f sin |
; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
α |
|
|
|
3) |
V1 |
2 g S1 |
f |
cos |
|
|
sin |
; |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
“1” |
α |
4) |
V1 |
2 g S1 |
sin |
f |
cos . |
||||||||||
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 14 |
|
|
|
|
|
|
|
|
|
|
Розв'язання. На вагонетку в процесі |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
руху діють сила тяжіння P |
mg , норма- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FОП |
|
f |
N . |
|
|
|
|||||||
льна реакція N похилої площини і сила опору руху FОП |
|
|
|
|
|||||||||||||||||||||||||
Ці сили сталі за величиною і сталі за напрямком по відношенню до напрямку переміщення вагонетки. Її далі будемо розглядати як точку, оскільки рух вагонетки поступальний. Із умови прикладу випливає, що сили, які діють
19

на точку, відомі, а треба знайти кінематичну характеристику її руху – швидкість V1 . Це друга задача динаміки точки, яку при сталих силах і заданому
переміщенні S1 можна розв’язати за допомогою теореми про зміну кінетич-
|
mV 2 |
|
mV 2 |
|
|
|
ної енергії точки, яка має вигляд |
1 |
|
0 |
A0 1 |
і формулюється таким |
|
2 |
2 |
|||||
|
|
|
||||
чином: зміна кінетичної енергії точки на деякому її переміщенні (із положення “0” в положення “1”) дорівнює алгебраїчній сумі робіт усіх діючих на точку сил на тому ж переміщенні. Тоді для даного приклада маємо:
mV 2 |
|
mV 2 |
|
|
|
1 |
|
0 |
A0 1, причому за умовою V0 |
= 0. |
|
2 |
2 |
||||
|
|
||||
Тут сума робіт діючих сил на заданому переміщенні точки S1 буде складатися із суми трьох доданків: A0 1 AP AN AFоп , а робота сталих сил
буде обчислюватись за спрощеною формулою – AF F S cos , де – кут між напрямком сили і напрямком переміщення.
Таким чином: |
A |
|
|
|
P S1 cos 90 |
|
mg S1 |
sin ; |
||||||||||||||
P |
|
|
||||||||||||||||||||
|
|
|
|
|
AN |
|
|
N S1 |
cos90 |
N S1 |
0 |
0 ; |
|
|
||||||||
|
AF |
оп |
Fоп S1 |
|
cos180 |
Fоп |
S1 |
1 |
Fоп |
|
S1 |
fN S1. |
||||||||||
Для визначення нормальної реакції площини N складемо рівняння рівно- |
||||||||||||||||||||||
ваги вагонетки відносно осі y (вагонетка вздовж осі |
y |
не переміщується): |
||||||||||||||||||||
Fy 0; |
N |
mg cos |
0; |
|
N |
mg cos . |
|
|
|
|
|
|||||||||||
Тоді |
AF |
оп |
f mg cos |
|
|
S1 і вираз теореми про зміну кінетичної енергії |
||||||||||||||||
точки приймає вигляд: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
mV |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
mg |
S1 |
sin |
|
f mg |
S1 cos |
|
; |
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
mV |
2 |
|
|
2mg S |
sin |
f cos . |
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|||||
Звідки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
V1 |
|
2 |
g |
S1 |
sin |
f cos |
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отже, правильною буде відповідь 4).
Приклад 10. Вказати правильну відповідь. Прискорення вільного падіння g прийняти рівним 10 м/с2. Обчислення проводити з точністю до трьох значущих цифр.
Якщо початкова швидкість візка (рис. 15) в положенні “0” становить V0 =9 м/с, то при R=5 м і φ1=75º його швидкість в кінцевому положенні “1” набуває значення:
|
|
|
|
|
|
|
|
|
|
|
1) V1 = 2,61 м/с; |
2) |
V1 = 0,97 м/с; |
|
|
|
|
|
|
|
|
|
|
|
|||
R |
|
|
φ1 |
V1 |
|
3) V1 = 1,52 м/с; |
4) |
V1 = 3,08 м/с. |
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Розв’язання. В даному прикладі розгляда- |
|||||
h |
|
|
|
|
|
|
|
|
|
“1” |
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
V0 |
|
|
|
|
ється рух візка як точки у вертикальній пло- |
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
“0”
Рис. 15
20
