МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УО «Белорусский государственный экономический университет»
Л.С. Барковская, Л.В. Станишевская, Ю.Н. Черторицкий
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Практикум
Издание второе, переработанное и дополненное
Часть 2
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Минск 2005
48
УДК 519.2 ББК 22.171 Б25
Ре ц е н з е н т ы: доктор физ.-мат. наук, профессор И.В. Белько; старший преподаватель В.Д.Петрович
Ре к о м е н д о в а н о кафедрой высшей математики
Ут в е р ж д е н о Редакционно-издательским советом университета
Барковская Л.С.
Б25 Теория вероятностей: Практикум / Л.С. Барковская, Л.В. Станишевская, Ю.Н. Черторицкий. — Мн.: БГЭУ, 2005. — 142 с.
ISBN 985-484-065-4.
УДК 519.2 ББК 22.171
ISBN 985-484-065-4
©Барковская Л.С., Станишевская Л.В., Черторицкий Ю.Н., 2005
©УО «Белорусский государственный экономический университет», 2005
49
СОДЕРЖАНИЕ
ВЕРОЯТНОСТЬ. ОСНОВНЫЕ ТЕОРЕМЫ ТЕО-
РИИ ВЕРОЯТНОСТЕЙ …………...………………..... 4
1.Пространство элементарных событий. Операции над случайными событиями ……………….…...... 4
2.Элементы комбинаторики. Непосредственный подсчет вероятностей .............................................. 9
3.Геометрические вероятности …………....……..... 20
4. |
Теоремы сложения и умножения вероятностей |
25 |
5. |
Формула полной вероятности и формула Байеса |
35 |
6. |
Повторные независимые испытания (схема Бер- |
|
|
нулли) …….............................................………….. |
41 |
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ….......……………….... |
51 |
|
7. |
Дискретная случайная величина ………......…... |
51 |
8.Непрерывные случайные величины. Плотность вероятности ……...............................................…... 71
9.Закон больших чисел …………......…………….... 118
10.Распределение функции одного и двух случай-
ных аргументов ……............................................... 125
ПРИЛОЖЕНИЯ …………………………………….... 139 ЛИТЕРАТУРА ………………………………………... 142
50
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
7. Дискретная случайная величина
Случайной называют величину, которая в результате испытания примет одно и только одно из возможных значений, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Обозначают случайные величины буквами Х, Y, Z, а их возможные значе-
ния — х, у, z.
Дискретной называют случайную величину, которая принимает отдельные, изолированные друг от друга значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным, но счетным.
Дискретная случайная величина может быть задана рядом распределения — это соответствие между возможными значениями и их вероятностями:
Х |
x1 |
x2 |
… |
xn |
Р |
p1 |
p2 |
… |
pn |
pi = P(X = xi ), i =1, n .
События X = x1, X = x2, …, X = xn образуют полную группу, следовательно, сумма вероятностей этих событий равна единице:
p1 + p2 + p3 +…pn =1.
Ряд распределения дискретной случайной величины можно изобразить графически в виде полигона или многоугольника распределения вероятностей. Для этого по горизонтальной оси в выбранном масштабе нужно отложить значения случайной величины, а по вертикальной — вероятности этих значений, тогда точки с координатами (xi , pi ) будут изображать полигон распределения
вероятностей; соединив же эти точки отрезками прямой, получим многоуголь-
ник распределения вероятностей.
51
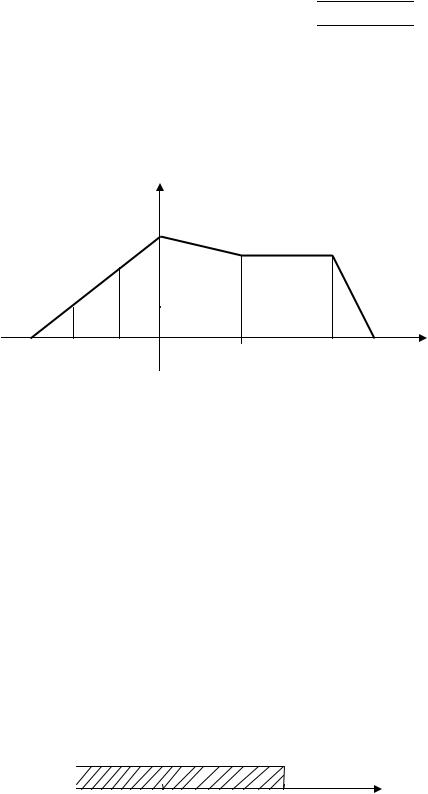
Пример 7.1. Пусть Х — дискретная случайная величина, заданная рядом распределения
Х |
–2 |
–1 |
0 |
2 |
4 |
Р |
0,1 |
0,2 |
0,3 |
0,2 |
0,2 |
Построить полигон и многоугольник распределения вероятностей. Решение. На оси Х откладываем значения xi , равные –2, –1, 0, 2, 4, а по
вертикальной оси вероятности этих значений (рис. 7.1):
y
|
|
|
|
|
0,3 |
|
|
А4 |
|
А5 |
|
|
|
|||||
|
|
. |
|
|
А3. |
|
|
|
|
|
|
|||||||
|
|
А2. |
|
|
0,2 . |
|
. |
|
|
|
||||||||
|
|
А1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
||
А0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
А6 |
x |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
||||||||||
|
||||||||||||||||||
Рис. 7.1
Точки A1, A2 , A3 , A4 , A5 изображают полигон распределения, а ломаная A0 A1 A2 A3 A4 A5 A6 — многоугольник распределения вероятностей.
Дискретная случайная величина может быть задана функцией распределения. Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение меньшее х:
F(x)= P(X < x)
Функцию F(x) иногда называют интегральной функцией распределения. Если значения случайной величины — точки на числовой оси, то геометрически функция распределения интерпретируется как вероятность того, что
случайная величина Х попадает левее заданной точки х (рис. 7.2):
|
Х< x |
|
0 |
х |
х |
Рис. 7.2
52
F(x) обладает свойствами:
1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей:
0 ≤ F(x)≤1.
Утверждение следует из того, что функция распределения — это вероятность.
2. Функция распределения есть неубывающая функция на всей числовой
оси.
3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна 1, т.е.
F(− ∞)= lim |
F(x)= 0 ; F(+ ∞)= lim F(x)=1. |
x→−∞ |
x→+∞ |
4. Вероятность попадания случайной величины в интервал [x1, x2 ) (включая x1 ) равна приращению ее функции распределения на этом интервале, т.е.
P(x1 ≤ X < x2 )= F(x2 )− F(x1 ).
Числовые характеристики случайной величины
Математическое ожидание М(Х) дискретной случайной величины
Пусть случайная величина Х может принимать только значения x1, x2 ,…, xn, вероятности которых соответственно равны p1, p2 ,…, pn . Тогда математическое ожидание М(Х) случайной величины Х определяется равенством
M (X )= x1p1 + x2 p2 |
n |
+…+ xn pn = ∑xi pi . |
|
|
i=1 |
Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина.
Математическое ожидание приближенно равно среднему арифметическому значений случайной величины: X ≈ M (X ).
Свойства математического ожидания
1. Математическое ожидание постоянной величины равно самой постоянной
53
M (C)= C .
2. Постоянный множитель можно выносить за знак математического ожидания
M (CX )= CM (X ).
3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий
M (X ±Y )= M (X )± M (Y ).
4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий
M (XY )= M (X )M (Y ).
5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю
M (X − M (X ))= 0.
Дисперсия случайной величины
Только математическое ожидание не может в достаточной степени характеризовать случайную величину.
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения.
Дисперсией D(X ) случайной величины Х называется математическое ожидание квадрата ее отклонения от ее математического ожидания:
D(X )= M [X − M (X )]2 .
Дисперсия — это мера рассеяния случайной величины около ее математического ожидания.
Если Х — дискретная случайная величина, то дисперсию вычисляют по следующим формулам:
D(X )= ∑n (xi − a)2 pi ,
i =1
где а = М(Х);
D(X )= M (X 2 )− (M (X ))2 .
54
Свойства дисперсии случайной величины
1. Дисперсия постоянной величины С равна нулю
D(C)= 0.
2.Постоянный множитель можно выносить за знак дисперсии, возводя его
вквадрат
D(CX )=C 2 D(X ).
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин
D(X +Y )= D(X )+ D(Y ).
4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий
D(X −Y )= D(X )+ D(Y ).
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.
Средним квадратическим отклонением σ случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии
σ = D(X ).
Среднее квадратическое отклонение характеризует степень отклонения случайной величины от ее математического ожидания и имеет размерность значений случайной величины.
Рассмотрим некоторые распределения дискретной случайной величины.
Биномиальный закон распределения
Если вероятность появления события А в каждом испытании постоянна и равна р, то число появлений события А — дискретная случайная величина Х,
принимающая значения 0, 1, 2, …, m, …, n с вероятностями Pn (m)= Cnm pmqn−m (формула Бернулли), где 0 < p <1, q =1 − p , m = 0,1, …, n .
Математическое ожидание и дисперсия случайной величины Х, распределенной по биномиальному закону, вычисляется по формулам:
M (X )= np ,
D(X )= npq .
55
Распределение Пуассона
Если число испытаний велико, а вероятность появления события р в каждом испытании очень мала, то вместо формулы Бернулли пользуются приближенной формулой Пуассона
Pn (m)≈ λme−λ , m!
где m −число появлений события в n независимых испытаниях; m принимает значения 0,1, 2, …, n . λ = np (среднее число появлений события в n испытаниях).
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ, который определяет этот закон, т.е.
M (X )= D(X )= λ .
Геометрическое распределение
Дискретная случайная величина X ление, если она принимает значения 1, множество значений) с вероятностями
= m имеет геометрическое распреде- 2, …, m, …(бесконечное, но счетное
P = (X = m) = pqm−1 ,
где 0 < p <1, q =1 − p, m =1, 2,... .
Определение геометрического распределения корректно, так как сумма
|
∞ |
∞ |
|
|
|
1 |
|
p |
|
|
вероятностей |
∑pi =∑pqi−1 = p |
|
|
= |
=1. |
|
||||
1 |
− q |
|
|
|||||||
|
i=1 |
i=1 |
|
|
p |
|
||||
Случайная величина |
X = m , |
имеющая геометрическое распределение, |
пред- |
|||||||
ставляет собой число |
m испытаний, проведенных по схеме Бернулли, с веро- |
|||||||||
ятностью р |
наступления события в каждом испытании до первого положи- |
|||||||||
тельного исхода. |
|
|
|
|
|
|
|
|
|
|
Математическое ожидание и дисперсия случайной величины Х , |
имею- |
|||||||||
щей геометрическое распределение с параметром р вычисляются по формулам:
M (X ) = 1p ,
D(X ) = pq2 ,
где q =1 − p.
56
Гипергеометрическое распределение
Пусть имеется N элементов, из которых М элементов обладают некоторым признаком А. Извлекаются случайным образом без возвращения n элементов. Х — дискретная случайная величина, число элементов обладающих признаком А, среди отобранных n элементов. Вероятность, что Х = m определяется по формуле
( ) C m C n−−m
P X = m = M N M .
CNn
Математическое ожидание и дисперсия случайной величины, распределенной по гипергеометрическому закону, определяются формулами:
M (X )= n MN ,
D(X )= n |
M |
|
M |
|
n −1 |
|
||
1 |
− |
1 |
− |
|
|
. |
||
N −1 |
||||||||
|
N |
|
N |
|
|
|||
Пример 7.2. В аккредитации участвуют 4 коммерческих вуза. Вероятности пройти аккредитацию и получить сертификат для этих вузов, соответственно равны 0,5; 0,4; 0,3; 0,2. Составить закон распределения числа коммерческих вузов, не прошедших аккредитацию. Найти числовые характеристики этого распределения.
Решение. В качестве случайной величины Х выступает число коммерческих вузов, не прошедших аккредитацию. Возможные значения, которые может принять случайная величина Х: 0, 1, 2, 3, 4.
Для составления закона распределения необходимо рассчитать соответствующие вероятности. Обозначим через событие A1 — первый вуз прошел ак-
кредитацию, A2 — второй, A3 — третий, A4 — четвертый. Тогда P(A1 )= 0,5; P(A2 )= 0,4 ; P(A3 )= 0,3; P(A4 )= 0,2 . Вероятности для вузов не пройти аккредитацию соответственно равны P(A1 )=1 − 0,5 = 0,5 ; P(A2 )=1 − 0,4 = 0,6 ; P(A3 )=
=1 − 0,3 = 0,7 ; P(A4 )=1 − 0,2 = 0,8 .
Тогда имеем:
P(X = 0)= P(A1A2 A3A4)= 0,012 .
P(X =1)= P(A1A2A3A4)+ P(A1A2 A3A4)+ P(A1A2 A3A4)+ P(A1A2 A3 A4)= 0,106.
57
P(X = 2)= P(A1A2 A3A4)+ P(A1A2 A3A4)+ P(A1A2 A3 A4)+ P(A1A2 A3A4)+
+ P(A1A2 A3 A4)+ P(A1A2 A3A4)= 0,320.
P(X =3)= P(A1A2A3A4)+ P(A1A2 A3A4)+ P(A1A2 A3 A4)+ P(A1A2 A3A4)= 0,394.
P(X = 4)= P(A1A2 A3A4)= 0,168.
Запишем закон распределения в виде таблицы
|
Х |
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
|
Р |
|
|
|
|
0,012 |
0,106 |
0,320 |
0,394 |
0,168 |
|
|
Проверка: 0,012 + 0,106 + 0,32 + 0,394 + 0,168 = 1. |
|
|
||||||||||
Вычислим |
|
|
|
|
|
|
|
|
|
|
|
|
M (X )= ∑n |
x p |
i |
|
= 0 0,012 +1 0,106 + 2 0,320 + 3 0,394 + 4 0,168 = 2,6 . |
||||||||
|
i =1 |
|
i |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
Вычислим D(X )= M (X 2 )− (M (X ))2 : |
|
|
|
|||||||||
M (X 2 )= ∑n |
x 2 p |
i |
= 0 0,012 +1 0,106 + 4 0,32 + 9 0,394 +16 0,168 = 7,62 , |
|||||||||
|
i =1 |
|
i |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
(M (X ))2 = 2,62 = 6,76 . D(X )= 7,62 − 6,76 = 0,86 .
Пример 7.3. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Составить закон распределения числа библиотек, которые последовательно посетит студент, чтобы взять необходимую книгу, если в городе 3 библиотеки.
Решение. В качестве случайной величины Х выступает число библиотек, которые посетит студент, чтобы получить необходимую книгу. Возможные значения, которые примет случайная величина Х: 1, 2, 3.
Обозначим через событие A1 — книга свободна в первой библиотеке, A2 — во второй, A3 — в третьей. Тогда P(A1 )= P(A2 )= P(A3 )= 0,3 . Вероятность противоположного события, что книга занята P (A1 )= P (A2 )= P (A3 )= =1 − 0,3 = 0,7 .
Для составления закона распределения рассчитаем соответствующие вероятности:
58
P(X =1)= P(A1 )= 0,3 ,
P(X = 2)= P(A1A2)= P(A1)P(A2)= 0,7 0,3 = 0,21,
P(X =3)= P(A1A2 A3)+ P(A1A2 A3)= P(A1)P(A2)P(A3)+ P(A1)P(A2)P(A3)= = 0,7 0,7 0,3 + 0,7 0,7 0,7 = 0,147 + 0,343 = 0,49.
Запишем закон распределения в виде таблицы.
Х |
1 |
2 |
3 |
Р |
0,3 |
0,21 |
0,49 |
Проверка: 0,3 + 0,21 + 0,49 = 1.
Пример 7.4. Из поступающих в ремонт 10 часов 7 нуждаются в общей чистке механизма. Часы не рассортированы по виду ремонта. Мастер, желая найти часы, нуждающиеся в чистке, рассматривает их поочередно и, найдя такие часы, прекращает дальнейший просмотр. Составить закон распределения числа просмотренных часов. Найти математическое ожидание и дисперсию этой случайной величины.
Решение. В качестве случайной величины Х выступает число просмотренных часов. Возможные значения, которые примет случайная величина Х: 1, 2, 3, 4. Все значения случайной величины зависимы.
Для составления закона распределения вычислим вероятности того, что случайная величина примет каждое из своих возможных значений. Для расчета вероятностей будем использовать формулу классической вероятности и теорему умножения для зависимых событий.
Пусть событие A1 — первые, взятые наугад, часы, нуждающиеся в чистке, A2 — вторые, A3 — третьи, A4 — четвертые. Тогда имеем:
P(X =1)= P(A1 )=107 ,
P(X = 2)= P(A1A2)= P(A1)P(A2)=103 79 = 307 ,
P(X =3)= P(A1A2 A3)= P(A1)P(A2)P(A3)=103 92 78 =1207 ,
59
P(X = 4)= P(A1A2 A3A4)= P(A1)P(A2)P(A3)P(A4)=103 92 18 77 =1201 .
Запишем закон распределения в виде таблицы
Х |
1 |
|
2 |
|
3 |
|
4 |
|
||||
Р |
|
7 |
|
|
7 |
|
|
7 |
|
|
1 |
|
|
10 |
|
30 |
|
120 |
|
120 |
|
||||
n
Проверим, что ∑ pi =1:
i =1
7 |
+ |
7 |
+ |
|
7 |
+ |
|
1 |
= |
84 + 28 + 7 +1 |
= |
120 |
=1. |
|
10 |
30 |
120 |
120 |
120 |
120 |
|||||||||
|
|
|
|
|
|
|||||||||
Вычислим математическое ожидание случайной величины по формуле
M (X )= ∑n |
x p |
|
=1 |
|
7 |
+ 2 |
7 |
+ 3 |
|
7 |
+ 4 |
|
1 |
= |
33 |
= |
11 . |
|
10 |
30 |
120 |
120 |
24 |
||||||||||||
i =1 |
i |
i |
|
|
|
|
|
|
8 |
||||||||
Вычислим дисперсию случайной величины по формуле
D(X )= M (X 2 )− (M (X ))2 .
Вычислим M (X 2 )=1 107 + 4 307 + 9 1207 +16 1201 = 5524 ,
D(X )= |
55 |
|
33 |
|
2 |
55 |
|
1089 |
|
231 |
|
77 |
. |
||
|
− |
= |
|
− |
|
= |
|
= |
|
|
|||||
24 |
24 |
576 |
576 |
192 |
|||||||||||
|
|
24 |
|
|
|
|
|
|
|||||||
Пример 7.5. Известно, что в определенном городе 20 % горожан добираются на работу личным автотранспортом. Случайно выбраны 4 человека. Составить закон распределения числа людей, добирающихся на работу личным автотранспортом. Найти числовые характеристики этого распределения. Написать функцию распределения и построить ее график.
Решение. В качестве случайной величины Х выступает число людей в выборке, которые добираются на работу личным автотранспортом. Возможные значения, которые может принять случайная величина Х: 0, 1, 2, 3, 4.
Вероятность того, что каждый из отобранных людей, которые добираются на работу личным автотранспортом, постоянна и равна p = 0,2 . Вероятность
противоположного события, т.е. того, что каждый из отобранных людей добирается на работу не личным автотранспортом, равна q =1 − p =1 − 0,2 = 0,8 . Все
4 испытания независимы. Случайная величина X = m подчиняется биномиаль-
60
ному закону распределения вероятностей с параметрами n = 4; p = 0,2 ; q = 0,8.
Для составления закона распределения вычислим вероятности того, что случайная величина примет каждое из своих возможных значений.
Расчет искомых вероятностей осуществляется по формуле Бернулли:
P |
(m)=Cm pmqn−m = |
n! |
pmqn−m . |
|
|||
n |
n |
m!(n − m)! |
|
|
|
||
P(X = 0)= P4 (0)=C40 0,20 0,84−0 =1 1 0,84 = 0,4096 , P(X =1)= P4 (1)=C41 0,21 0,84−1 = 4 0,2 0,83 = 0,4096 ,
P(X = 2)= P4 (2)=C42 0,22 0,84−2 = 6 0,22 0,82 = 0,1536 ,
P(X =3)= P4 (3)=C43 0,23 0,84−3 = 4 0,23 0,8 = 0,0256 , P(X = 4)= P4 (4)=C44 0,24 0,84−4 =1 0,24 1 = 0,0016 .
Запишем закон распределения в виде таблицы
Х |
0 |
1 |
2 |
3 |
4 |
Р |
0,4096 |
0,4096 |
0,1536 |
0,0256 |
0,0016 |
Так как все возможные значения случайной величины образуют полную группу событий, то сумма их вероятностей должна быть равна 1.
Проверка: 0,4096 + 0,4096 + 0,1536 + 0,0256 + 0,0016 = 1.
Найдем числовые характеристики дискретной случайной величины: математическое ожидание, дисперсию и среднее квадратическое отклонение. Математическое ожидание может быть рассчитано по формуле
M (X )= ∑n |
x p |
i |
= 0 0,4096 +1 0,4096 + 2 0,1536 + 3 0,0256 + 4 0,0016 = 0,8 . |
i =1 |
i |
|
|
|
|
|
Так как случайная величина подчиняется биноминальному закону, то для расчета математического ожидания можно воспользоваться формулой
M (X )= np = 4 0,2 = 0,8 .
Дисперсия случайной величины может быть рассчитана по формуле D(X )=
= M (X 2 )− (M (X ))2 :
|
|
|
(M (X ))2 = 0,82 = 0,64 , |
M (X 2 )= ∑n |
x 2 p |
i |
= 0 0,4096 +1 0,4096 + 4 0,1536 + 9 0,0256 +16 0,0016 =1,28, |
i =1 |
i |
|
|
|
|
|
|
|
|
|
D(X )=1,28 − 0,64 = 0,64 . |
|
|
|
61 |
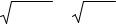
В данном случае дисперсию можно рассчитать по формуле
D(X )= npq = 4 0,2 0,8 = 0,64.
Рассчитаем среднее квадратическое отклонение случайной величины по формуле
у = D(X )= 0,64 = 0,8.
Составим функцию распределения случайной величины Х по формуле
F(x)= P(X < x).
1.x ≤ 0, F(x)= 0.
2.0 < x ≤1, F(x)= 0,4096 .
3.1 < x ≤ 2, F(x)= 0,4096 + 0,4096 = 0,8192 .
4.2 < x ≤3, F(x)= 0,4096 + 0,4096 + 0,1536 = 0,9728.
5.3 < x ≤ 4, F(x)= 0,4096 + 0,4096 + 0,1536 + 0,0256 = 0,9984 .
6.x > 4, F(x)=1.
Запишем функцию распределения
0, |
x ≤ 0; |
|
0,4096, |
0 < x ≤1; |
|
|
|
|
F(x)= 0,8192, |
1 < x ≤ 2; |
|
0,9728, |
2 < x ≤3; |
|
0,9984, |
3 < x ≤ 4; |
|
|
x > 4. |
|
1, |
|
|
График функции распределения вероятностей имеет ступенчатый вид (рис. 7.3). Скачки равны вероятностям, с которыми случайная величина принимает возможные значения.
62
F(х)
1
0,9984
0,9728
0,8192
0,4096
0 |
1 |
2 |
3 |
4 |
х |
Рис. 7.3
Пример 7.6. Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0,1. Составить закон распределения числа возвращенных в срок кредитов из 5 выданных. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
Решение. В качестве случайной величины Х выступает число кредитов, возвращенных клиентами в срок. Возможные значения, которые может принять случайная величина Х: 0, 1, 2, 3, 4, 5.
Вероятность того, что каждый клиент возвратит кредит в срок, постоянна и равна p = 0,9. Вероятность того, что кредит не будет возвращен в срок, равна
q =1 − 0,9 = 0,1. Все 5 испытаний независимы. Случайная величина подчиняется биномиальному распределению с параметрами n = 5 ; p = 0,9 ; q = 0,1; X = m .
Для составления закона распределения вычислим вероятности того, что случайная величина примет каждое из своих возможных значений. Расчет искомых вероятностей осуществляется по формуле Бернулли
Pn(m)=Cnm pmqn−m ,
P(X = 0)= P5 (0)=C50 0,90 0,15 = 0,15 = 0,00001,
P(X =1)= P5 (1)=C51 0,91 0,14 =5 0,9 0,14 = 0,00045 ,
P(X = 2)= P5 (2)=C52 0,92 0,13 =10 0,92 0,13 = 0,0081,
63
P(X =3)= P5(3)=C53 0,93 0,12 =10 0,93 0,12 = 0,0729 , P(X = 4)= P5 (4)=C54 0,94 0,11 =5 0,94 0,1 = 0,32805 , P(X =5)= P5 (5)=C55 0,95 0,10 = 0,95 = 0,59049 .
Запишем закон распределения в виде таблицы
Х |
0 |
1 |
2 |
3 |
4 |
5 |
Р |
0,00001 |
0,00045 |
0,0081 |
0,0729 |
0,32805 |
0,59049 |
Математическое ожидание вычислим по формуле
M (X )= np =5 0,9 = 4,5 .
Дисперсию вычислим по формуле
D(X )= npq =5 0,1 0,9 = 0,45 .
Пример 7.7. Из 10 телевизоров на выставке оказались 4 телевизора фирмы «Сони». Наудачу для осмотра выбраны 3 телевизора. Составить закон распределения числа телевизоров фирмы «Сони» среди 3 отобранных.
Решение. В качестве случайной величины Х выступает число телевизоров фирмы «Сони». Возможные значения, которые может принять случайная величина Х: 0, 1, 2, 3. Для составления закона распределения вычислим вероятности того, что случайная величина примет каждое из своих возможных значений. Эти
вероятности можно рассчитать по формуле классической вероятности p = mn :
|
P(X = 0)= C40C63 |
= |
|
1 |
|
P(X = 2)= C42C61 |
= |
|
3 |
|
; |
|
||||||||||
|
10 |
|
||||||||||||||||||||
|
|
C3 |
|
|
|
6 |
|
|
|
|
|
C3 |
|
|
|
|
|
|
||||
|
|
10 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|||||
|
P(X =1)= C41C62 |
= |
1 |
|
P(X =3)= C43C60 |
= |
1 |
. |
|
|||||||||||||
30 |
||||||||||||||||||||||
|
|
C3 |
|
|
2 |
|
|
|
|
C3 |
|
|
|
|
|
|
||||||
|
|
10 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
||||
Запишем закон распределения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
0 |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
3 |
|
||||
|
Р |
1 |
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
1 |
|
||
|
|
6 |
|
|
|
|
|
2 |
|
10 |
|
|
|
|
|
|
30 |
|
||||
Убедимся, что ∑pi = 1 + 1 + 3 |
|
+ 1 |
= 5 +15 + 9 +1 = 30 =1. |
|||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
6 2 |
|
10 |
|
30 |
30 |
|
|
|
30 |
|
|
|
||||||||
64
Пример 7.8. На двух автоматических станках производятся одинаковые изделия. Даны законы распределения числа бракованных изделий, производимых в течение смены на каждом из них:
Х: для первого
|
|
Х |
0 |
|
1 |
2 |
3 |
|
|||
|
|
Р |
0,1 |
|
0,6 |
0,2 |
0,1 |
|
|||
Y: для второго |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
y j |
|
0 |
|
1 |
|
2 |
|
|
|
Р |
|
p j |
|
0,5 |
|
0,3 |
|
0,2 |
|
Составить закон распределения числа производимых в течение смены бракованных изделий обоими станками. Проверить свойство математического ожидания суммы случайных величин.
Решение. Для того чтобы составить закон распределения Х + Y необходимо складывать xi + y j , а соответствующие им вероятности умножить pi p j :
x1 |
+ y1 = 0 + 0 |
= 0 ; |
p0 = 0,1 0,5 = 0,05, |
|
||
x1 |
+ y2 |
= 0 +1 |
=1; |
p1 = 0,1 0,3 + 0,6 0,5 = 0,33 , |
||
x1 |
+ y3 |
= 0 + 2 = 2 ; |
p2 = 0,1 0,2 + 0,6 0,3 + 0,2 0,5 = 0,3, |
|||
x2 |
+ y1 =1 + 0 |
=1; |
p3 = 0,6 0,2 + 0,2 0,3 |
+ 0,1 0,5 = 0,23, |
||
x2 |
+ y2 =1 +1 |
= 2 ; |
p4 = 0,2 0,2 + 0,1 0,3 |
= 0,07 , |
||
x2 |
+ y3 =1 + 2 =3; |
p5 = 0,1 0,2 = 0,02 , |
|
|||
x3 + y1 = 2 + 0 = 2 , x3 + y2 = 2 +1 =3 , x3 + y3 = 2 + 2 = 4 , x4 + y1 =3 + 0 =3 , x4 + y2 =3 +1 = 4 ,
x4 + y3 =3 + 2 =5.
65
Закон распределения запишем в виде таблицы
Х + Y |
0 |
|
1 |
|
2 |
3 |
4 |
5 |
|
|
P |
0,05 |
|
0,33 |
0,3 |
0,23 |
0,07 |
0,02 |
|
||
Проверим свойство математического ожидания M (X +Y )= M (X )+ M (Y ): |
||||||||||
|
M (X )= ∑n |
x p |
i |
= 0 0,1 +1 0,6 + 2 0,2 + 3 0,1 =1,3, |
|
|
||||
|
|
i =1 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M (Y )= ∑n y j p j = 0 0,5 +1 0,3 + 2 0,2 = 0,7 ,
j=1
M (X +Y )= 0 0,05 +1 0,33 + 2 0,3 + 3 0,23 + 4 0,07 + 5 0,02 = 2 ,
M (X )+ M (Y )=1,3 + 0,7 = 2 .
Пример 7.9. Дискретная случайная величина Х имеет только два возможных значения: x1 и x2 , причем x2 > x1 . Вероятность того, что Х примет значение
x1 , равна 0,6. Найти закон распределения величины Х, если математическое ожидание M (X )=1,4 ; D(X )= 0,24 .
Решение. Сумма вероятностей всех возможных значений случайной величины равна единице, поэтому вероятность того, что Х примет значение x2 =1 − 0,6 = 0,4 . Напишем закон распределения Х
|
X |
|
|
x1 |
|
|
|
x2 |
|
|
|
|
|
|
P |
|
|
0,6 |
|
|
|
0,4 |
|
|
|
|
|
Для того чтобы отыскать x1 и x2 |
необходимо составить два уравнения. Из |
||||||||||||
условия задачи следует, что M (X )= 0,6x + 0,4x |
2 |
=1,4 , |
D(X )= 0,6x 2 |
+ 0,4x |
2 |
− |
|||||||
|
|
|
|
1 |
|
|
|
1 |
|
2 |
|
||
−1,42 = 0,24 . |
|
|
|
|
|
|
|
|
|
|
|
||
Составим систему уравнений |
|
|
|
|
|
|
|
|
|
|
|
||
|
0,6x1 + 0,4x2 =1,4, |
|
|
|
|
|
|
|
|||||
|
0,6x 2 + 0,4x 2 |
= 2,2. |
|
|
|
|
|
||||||
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
Решив эту систему, имеем x1 =1; |
x2 = 2 |
и x1 =1,8 ; |
x2 = 0,8 . |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
66 |
По условию x2 > x1 , поэтому задаче удовлетворяет лишь первое решение, т.е. x1 =1; x2 = 2 . Тогда закон распределения имеет вид
X |
1 |
2 |
P |
0,6 |
0,4 |
Пример 7.10. Случайные величины X и Y независимы. Найти дисперсию случайной величины Z = 2X + 3Y , если известно, что D(X )= 4 , D(Y )=5 .
Решение. Так как имеют место свойства дисперсии
D(X +Y )= D(X )+ D(Y ) и D(CX )=C 2 D(X ), то получим
D(Z )= D(2X )+ D(3Y )= 22 D(X )+ 32 D(Y )= 4 4 + 9 5 =16 + 45 = 61.
Задачи для самостоятельного решения
7.1. Среди 10 изготовленных приборов 3 неточных. Составить закон распределения числа неточных приборов среди взятых наудачу 4 приборов. Найти математическое ожидание и дисперсию этой случайной величины. Составить функцию распределения случайной величины и построить ее график.
Ответ:
X |
0 |
1 |
|
2 |
|
3 |
|||
P |
1 |
|
1 |
|
|
3 |
|
|
1 |
|
6 |
2 |
|
10 |
|
30 |
|||
M (X )=1,2 ; D(X )= 0,56 . |
|
|
0 |
при |
x (− ∞; 0], |
|
при |
x (0;1], |
1 |
||
6 |
|
|
F(x)= 2 |
при |
x (1; 2], |
3 |
|
|
29 |
при |
x (2; 3], |
30 |
|
x (3; + ∞). |
1 |
при |
|
|
|
|
67
7.2. В магазине продаются 5 отечественных и 3 импортных телевизора. Составить закон распределения случайной величины — числа импортных из 4 наудачу взятых телевизоров. Найти функцию распределения и построить ее график.
Ответ:
X |
0 |
|
1 |
2 |
3 |
||
P |
|
1 |
|
3 |
3 |
|
1 |
|
14 |
|
7 |
7 |
14 |
||
0 |
при x (−∞; 0], |
||||
|
|
|
|||
|
1 |
при |
x (0;1], |
||
14 |
|||||
F(x)= |
1 |
|
при |
x (1; 2], |
|
|
|||||
2 |
|
|
|||
13 |
при |
x (2; 3], |
|||
|
|
|
|||
14 |
|||||
|
|
||||
|
при |
x (3; +∞). |
|||
1 |
|||||
|
|
|
|||
7.3. В билете три задачи. Вероятность правильного решения первой задачи равна 0,9, второй — 0,8, третьей — 0,7. Составить закон распределения числа правильно решенных задач в билете и вычислить математическое ожидание и дисперсию.
Ответ:
X |
0 |
1 |
2 |
3 |
P |
0,006 |
0,092 |
0,398 |
0,504 |
M (X )= 2,4;
D(X )= 0,46 .
7.4. Поступающий в институт должен сдать 3 экзамена. Вероятность сдачи первого экзамена 0,9, второго — 0,8, третьего — 0,7. Следующий экзамен поступающий сдает только в случае успешной сдачи предыдущего. Составить закон распределения числа приходов на экзамен для лица, поступающего в институт. Найти математическое ожидание случайной величины.
Ответ:
X |
1 |
2 |
3 |
P |
0,1 |
0,18 |
0,72 |
|
M (X )= 2,62 . |
|
|
68
7.5. В городе 4 коммерческих банка. У каждого риск банкротства в течение года составляет 10 %. Составить закон распределения числа банков, которые могут обанкротиться в течение следующего года и найти числовые характеристики этого распределения.
Ответ:
X |
0 |
1 |
2 |
3 |
4 |
P |
0,6561 |
0,2916 |
0,0486 |
0,0036 |
0,0001 |
M (X )= 0,4 ;
D(X )= 0,36 ;
у(X )= 0,6.
7.6. Вероятность поражения земляники вирусным заболеванием равна 0,2. Составить закон распределения числа кустов земляники, зараженных вирусом, из четырех посаженных кустов. Найти математическое ожидание и дисперсию этой случайной величины.
Ответ:
X |
0 |
1 |
2 |
3 |
4 |
P |
0,4096 |
0,4096 |
0,1536 |
0,0256 |
0,0016 |
M (X )= 0,8;
D(X )= 0,64 .
7.7. В урне находятся шары трех весов 3, 4 и 5 кг с соответствующими вероятностями 0,2; 0,3; 0,5. Извлекаются два шара с возвращением обратно. Составить закон распределения суммарного веса двух извлеченных шаров. Найти математическое ожидание и дисперсию этой случайной величины.
Ответ:
X |
6 |
7 |
8 |
9 |
10 |
P |
0,04 |
0,12 |
0,29 |
0,30 |
0,25 |
M (X )=8,6;
D(X )=1,22 .
69
7.8. Производится стрельба из орудия по удаляющейся цели. При первом выстреле вероятность попадания равна 0,8, при каждом следующем выстреле вероятность попадания уменьшается в 2 раза. Случайная величина Х — число попаданий в цель при трех выстрелах. Составить закон распределения случайной величины Х.
Ответ:
X |
0 |
1 |
2 |
3 |
P |
0,096 |
0,472 |
0,368 |
0,064 |
7.9. Найти закон распределения числа пакетов трех акций, по которым владельцем будет получен доход, если вероятность получения дохода по каждому из них равна соответственно 0,5; 0,6; 0,7. Найти математическое ожидание и дисперсию этой случайной величины.
Ответ:
X |
0 |
1 |
2 |
3 |
P |
0,06 |
0,29 |
0,44 |
0,21 |
M (X )=1,8 ;
D(X )= 0,7 .
7.10. Дискретная случайная величина Х может принимать только два значения x1 и x2 , причем x1 < x2 . Известны вероятность p1 = 0,1 возможного зна-
чения x1 , математическое ожидание M (X )=3,9 и дисперсия D(X )= 0,09 . Найти закон распределения этой случайной величины.
Ответ:
X |
3 |
4 |
P |
0,1 |
0,9 |
7.11.Два стрелка стреляют по одной мишени, делая независимо друг от друга по два выстрела. Вероятность попадания в мишень для первого стрелка равна 0,4, для второго – 0,5. Пусть Х – число попаданий в мишень первым стрелком, Y– число попаданий в мишень вторым стрелком. Построить закон распределения случайной величины Z = X – Y и найти M(Z), D(Z).
Ответ: M(Z) = –0,2; D(Z) = 0,98.
7.12.Имеется шесть ключей, из которых только один подходит к замку. Составить закон распределения числа попыток при открывании зонта, если ис-
70
пробованный ключ в последующих опробованиях не участвует. Найти математическое ожидание и дисперсию этой случайной величины.
Ответ: M(Х) = 72 ; D(Х) = 1235 .
7.13.В магазин поступила обувь с двух фабрик в соотношении 2 : 3. Куплено четыре пары обуви. Построить закон распределения числа купленных пар обуви, изготовленных первой фабрикой. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
Ответ: M(Х) = 1,6; D(Х) = 0,96; σ(X ) = 0,9799 .
7.14.В партии из десяти изделий имеется одно бракованное. Чтобы его обнаружить выбирают наугад одно изделие за другим и каждое вынутое проверяют. Построить закон распределения и найти математическое ожидание числа проверенных изделий.
Ответ: M(Х) = 5,5.
7.15.Проводится проверка большой партии деталей до обнаружения бракованной (без ограничения числа проверенных деталей). Составить закон распределения числа проверенных деталей. Найти M(Х) и D(Х) случайной величины, если известно, что вероятность брака для каждой детали равна 0,1.
Ответ: M(Х) = 10;D(X)= 90.
7.16.Независимые случайные величины Х и Y заданы следующими законами распределения:
X |
5 |
2 |
4 |
P |
0,6 |
0,1 |
0,3 |
Y |
7 |
9 |
Р |
0,8 |
0,2 |
Найти M (X +Y ) , M (X Y ) и проверить, что M (X +Y ) = M (X ) + M (Y ) , = M (X ) M (Y ) .
Ответ: M (X +Y ) =11,8; M (X Y ) = 32,56.
8. Непрерывные случайные величины. Плотность вероятности
Функцией распределения случайной величины Х называется функция F(х), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х: F(x)= P(X < x).
71