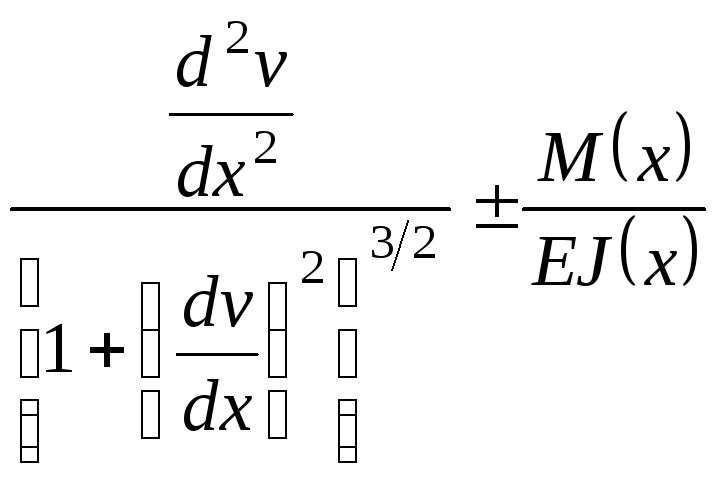Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Украинский Государственный химико-технологический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Тема 9.doc

Скачиваний:

Добавлен:

20.02.2016

Размер:

812.54 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 55

Підставляємо координату перерізу с (м) в рівняння (б). Отримаємо:

Після підстановки чисельного значенння жорсткості поперечного перерізу балки у вираз для кута повороту, маємо:

рад .

Знак “+” у кута повороту означає, що поворот перерізу відбувається за годинниковою стрілкою. Це правильно, тому що розв’язання задачі виконувалося в лівій системі координат.

Приклад 9.11. Визначити номер прокатного профілю з умови жорсткості для балки, зображеної на рис.9.15. Матеріал балки – сталь з модулем пружності МПа. Допустимий прогин складає, дем – прольот балки. Допустиме напруження для матеріалу балкиМПа.

Рис.9.15

Розв’язок:

1. Визначаємо опорні реакції. Для цього складаємо два рівняння рівноваги:

; (а);

. (б)

Розв’язучи рівняння (а) та (б) відносно реакцій, отримаємо: кН,кН.

2. Початок координат вибираємо на лівому кінці балки. Вісь прогинів спрямовуємо вгору, вісь праворуч.

3. Визначаємо початкові параметри. З двох початкових параметрів прогин на початку координат ; кут поворотузнайдемо, дорівнюючи нулю прогин на опорі В прим:

. (в)

Розв’зуючи рівняння (в) відносно , знаходимо:

. (г)

4. Визначаємо прогин посередині балки в перерізі С. Будемо вважати, що максимальний прогин (стріла прогину) виникає посередині прольоту. Переріз С належить першій ділянці, тому з універсального рівняння пружної лінії викреслюємо члени, що не належать першій ділянці, і отримаємо прим:

5. Знаходимо потрібний момент інерції перерізу з умови жорсткості:

. (д)

Допустимий прогин м. Підставляючи в умову жорсткості (д) модуль стріли прогину і величину допустимого прогину, маємо:

Звідки:

м⁴см⁴.

З сортаменту прокатної сталі вибираємо номер прокатного двотавру. Таким двотавром є двотавр №40 з моментом інерції см⁴ і моментом опору см³.

6. Виконуємо перевірку обраного двотавра на міцність. Максимальний згинальний момент, що діє в балці, дорівнює кНм (розрахунок максимального згинального моменту тут не наводиться). Підставляємо в умову міцності значення максимального згинального моментута моменту опоруі обчислюємо максимальне напруження, що діє в балці:

МПа.

Це напруження виявилося меньшим за допустиме МПа.

Отже, остаточно приймаємо двотавр №40, який задовольняє умовам як міцності, так і жорсткості.

9.5. Тести до теми №9 “Визначення переміщень при згинанні. Розрахунок балок на жорсткість” Таблиця 9.2

№	Питання	Час для відповіді, секунди
1	2	3
1	Що ми називаємо жорсткістю деталі машин або конструкції?	30
	1. Здатність чинити опір зовнішнім навантаженням, не руйнуючись?
	2. Здатністю чинити опір зовнішнім навантаженням без видимих деформацій?
	3. Здатність чинити опір великим деформаціям при малій зміні навантаження?
	4. Здатність деформуватися без порушення міцності?
2	Що називається деформацією тіла?	30
	1. Зміна положення тіла у просторі?
	2. Зміна теплопровідності тіла?
	3. Зміна вартості тіла?

Продовження таблиці 9.2
1	2	3
	4. Зміна форми і розмірів тіла?
3	Яке з переміщень поперечних перерізів не виникає при плоскому згинанні балки?	30
	1. Прогин.
	2. Кут повороту.
	3. Кут закручування.
	4. Поздовжнє переміщення.
4	Перша похідна від прогину по поздовжній координаті є:	30
	1. Синус кута повороту перерізу?
	2. Тангенс кута повороту перерізу?
	3. Косинус кута повороту перерізу?
	2. Котангенс кута повороту перерізу?
5	Яким з рівнянь описується зігнута вісь балки при плоскому поперечному згинанні?	30
	1. Алгебраїчним.
	2. Інтегральним.
	3. Диференціальним.
	4. Тригонометричним.
6	Яке з рівнянь є наближеним (основним) рівнянням пружної лінії балки?	30
	1.
	2.
	3.
	4.
7	Що роблять з основним диференціальним рівнянням пружної лінії балки при визначенні переміщень при плоскому поперечному згинанні?	30
	1. Диференціюють.

Продовження таблиці 9.2
1	2	3
	2. Розкладають у ряд.
	2. Інтегрують.
	3. Потенціюють.
8	Скільки разів потрібно проінтегрувати основне диференціальне рівняння пружної лінії балки, щоб одержати вираз для прогину ?	30
	1. Два рази.
	2. Три рази.
	3. Один раз.
	4. Чотири рази.
9	Скільки разів потрібно проінтегрувати основне диференціальне рівняння пружної лінії, щоб одержати вираз для кута повороту ?	30
	1. Два рази.
	2. Три рази.
	3. Один раз.
	4. Чотири рази.
10	Що собою являє рівняння:	30
	1. Вираз для згинального моменту .
	2. Вираз для поперечної сили .
	3. Вираз для кута повороту .
	4. Вираз для інтенсивності розподіленого навантаження .
	5. Вираз для прогину .
11	Що означає рівняння:	30
	1. Вираз для згинального моменту .
	2. Вираз для поперечної сили .
	3. Вираз для кута повороту .
	4. Вираз для інтенсивності розподіленого навантаження .
	5. Вираз для прогину .
12	Що означає рівняння:	30
	1. Вираз для згинального моменту .
	2. Вираз для поперечної сили .
	3. Вираз для кута повороту .
	4. Вираз для інтенсивності розподіленого навантаження .
Продовження таблиці 9.2
1	2	3
	5. Вираз для прогину .
13	Що можна визначити за допомогою виразу: ?	30
	1. Поперечну силу .
	2. Прогин .
	3. Інтенсивність розподіленого навантаження .
	4. Кут повороту .
	5. Згинальний момент .
14	Що можна визначити за допомогою виразу: ?	60
	1. Поперечну силу .
	2. Прогин .
	3. Інтенсивність розподіленого навантаження
	4. Кут повороту .
	5. Згинальний момент .
15	При інтегруванні основного диференціального рівняння пружної лінії використовують граничні умови. З якою метою?	30
	1. Для визначення меж зміни величини згинального моменту .
	2. Для визначення меж зміни величини поперечної сили .
	3. Для визначення меж зміни величини кута повороту .
	4. Для визначення меж зміни величини прогину .
	5. Для визначення значень сталих інтегрування ,.
16	Яка з епюр кутів повороту відповідає наведеній на рисунку епюрі прогинів?	120
	1.
	2.
	3.
Продовження таблиці 9.2
1	2	3
	4.
17	Яка з епюр прогинів відповідає наведеній на рисунку епюрі згинальних моментів?	120
	1.
	2.
	3.
	4.
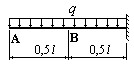
18	У скількі разів прогин у перерізі А на кінці зображеної на рисунку балки, більший, ніж прогин у перерізі В посередині балки?	240
	1. У 3 рази.
	2. У 3,5 рази.
	3. У 2,8 рази.
	4. У 3,2 рази.
19	У скількі разів кут повороту перерізу А на кінці зображеної на рисунку балки більший, ніж кут повороту перерізу В посередині балки?	300
	1. У 1,225 рази.
	2. У 1,143 рази.
	3. У 1,159 рази.
	4. У 1,137 рази.


Продовження таблиці 9.2
1	2	3
20	Знайти стрілу прогину (у мм) балки, зображеної на рисунку, якщо жорсткість поперечного перерізу балки дорівнює кНм².	240