Тема 9 визначення переміщень при згинанні. Розрахунок балок на жорскість

9.1. Уявлення про пружну лінію. Прогин і кут повороту. Диференціальне рівняння пружної лінії

Щоб мати уявлення про роботу балок, що згинаються, недостатньо знати тільки напруження, що виникають у перерізах балки від заданого навантаження. Обчислені напруження дозволяють перевірити міцність системи. Однак досить міцні балки можуть виявитися непридатними до експлуатації через недостатню жорсткість. Якщо балка під навантаженням сильно прогинається, то при експлуатації спорудження, що має гнучкі балки, з'являться ускладнення і, крім того, можуть виникнути коливання балки з великими амплітудами, а разом з тим і значні додаткові напруження.

Під жорсткістю треба розуміти здатність елементів конструкцій і деталей машин чинити опір зовнішнім навантаженням без суттєвих деформацій. Розрахунок на жорсткість полягає в оцінки пружної піддатливості балки під дією прикладених навантажень і підбір таких розмірів поперечного перерізу, при яких переміщення не будуть перевищувати встановлених нормами меж. Для виконання такого розрахунку необхідно навчитися обчислювати переміщення точок балки під дією будь-якого зовнішнього навантаження.

Розглянемо деформацію балки при простому згинанні. Вісь балки (Рис.9.1,а) під дією навантаження, розташованого в одній з головних площин інерції (у площині ), викривляється в тій самій площині, а поперечні перерізи повертаються й одночасно отримають поступальні переміщення. Викривлена вісь балки називаєтьсязігнутою віссю або пружною лінією. На рис. 9.1 пружна лінія зображена тонкою кривою.

Точка , що належить осі балки і розташована в перерізі на відстанівід початку координат, переміститься в точку. Позначимо переміщення довільної точки осі бруса в напрямку осічерез, а переміщення уздовж осі бруса– через. Якщо в точціпровести дотичну до осі вигнутої балки, то стосовно первісної осі вона буде повернена на кут. Одночасно на той самий кут повернеться переріз у точці. Таким чином, три величини ,іє компонентами переміщення довільного поперечного перерізу балки. Переміщенняцентра ваги перерізу уздовж напрямку, перпендикулярного до осі балки, називаєтьсяпрогином. Найбільший прогин називається стрілою прогину і позначається буквою .

Кут , на який кожний переріз повертається щодо свого первісного положення, називаєтьсякутом повороту перерізу. Як уже відзначалося, кут повороту також може бути визначений як кут між дотичною до пружної лінії і віссю .

Рис.9.1

Перевірка жорсткості балок зводиться до вимоги, щоб найбільший прогин не перевищував визначеної частки прольоту:

.

Число встановлюється нормами проектування приблизно в межах від 300 до 1000. Для відповідальних споруджень, наприклад, для залізничних мостів, величинаприймається рівною 1000.

Звідси видно, що прогини при згинанняі, як правило, малі у порівнянні з прольотом балки. Це дозволяє внести деякі спрощення. По-перше, при малих прогинах кут нахилу дотичної до зігнутої осі балки можна визначати за допомогою виразу:

. (9.1)

По-друге, горизонтальними переміщеннями можна знехтувати, тому що вони суттєво менші за(). У зв'язку з цим при розрахунках будемо користуватися умовною схемою переміщень, зображеною на рис.9.1,б. Відповідно до цієї схеми кожна точка переміщується перпендикулярно поздовжній осі бруса.

Для визначення повної картини деформацій необхідно одержати рівняння пружної лінії:

.

Виходячи з фізичної природи зігнутої осі балки, можемо стверджувати, що пружна лінія повинна бути неперервною і гладкою кривою, отже, вздовж всієї осі балки повинні бути неперервні функція і її перша похідна. Прогини та кути повороту і є переміщеннями перерізів балок при згинанні. Деформація тієї або іншої ділянки балки визначається викривленням її зігнутої осі, тобто кривизною.

При виведенні формули для нормальних напружень при згинанні в Темі №8 був отриманий зв'язок між кривизною і згинальним моментом:

. (9.2)

З курсу вищої математики відоме наступне рівняння кривизни плоскої кривої дорівнює:

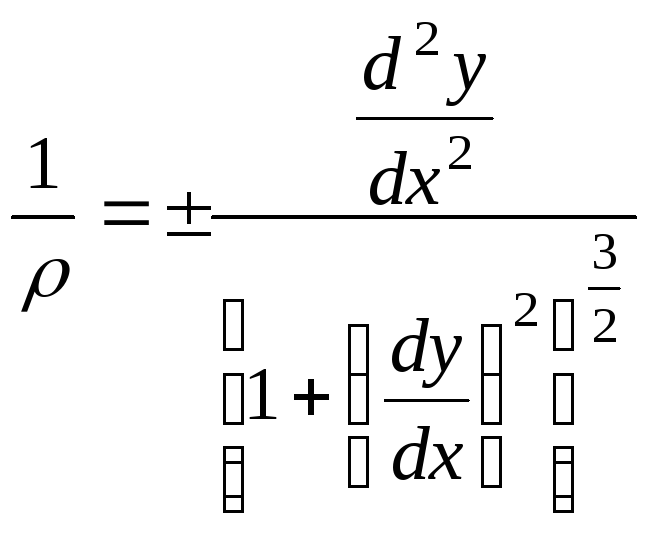. (9.3)

Підставляючи значення кривизни у вираз (9.2) і заміняючи координату прогином, одержимо точне диференціальне рівняння пружної лінії балки:

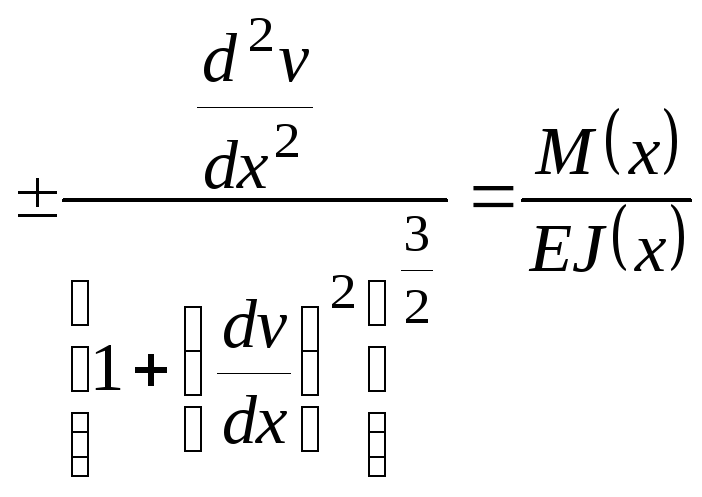. (9.4)

Інтегрування цього нелінійного диференціального рівняння пов'язане зі значними ускладненнями. З огляду на те, що на практиці доводиться мати справу з малими прогинами і що тангенси кутів нахилу дотичної до осі будуть малі, квадратом першої похідноїу порівнянні з одиницею можна знехтувати. Тоді одержимо наближене (основне) диференціальне рівняння:

. (9.5)

Два знаки у рівнянні (9.5) поставлені тому, що знак кривизни може не збігатися зі знаком згинального моменту. Знак кривизни залежить від напрямку осей координат. Знак згинального моменту був обраний в залежності від того, де розташовані розтягнуті волокна. Так, наприклад, для випадку, коли вісьспрямована вгору, додатному моменту (Рис.9.2,а) відповідає додатна кривизна, а від’ємному – від’ємна кривизна.

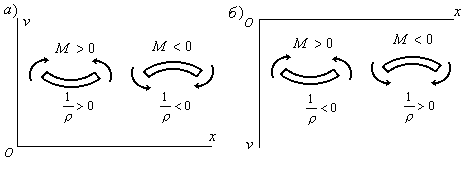
Рис 9.2

Таким чином, у випадку, коли вісь спрямована вгору, знаки кривизни і згинального моменту збігаються. Тому в диференціальному рівнянні береться знак “+”. Якщо вісьспрямована униз, то знаки кривизни і згинального моменту будуть різними (Рис.9.2,б). Тому в правій частині рівняння (9.5) береться знак “”.

9.2. Метод безпосереднього інтегрування наближеного (основного) диференціального рівняння пружної лінії

Розв’язуючи задачу аналітичним методом, кути повороту і прогиниобчислюють послідовним інтегруванням наближеного диференціального рівняння (9.5). Проінтегрувавши рівняння (9.5) перший раз, одержимо вираз для кута повороту:

, (9.6)

де  стала інтегрування.

Інтегруючи другий раз, одержимо вираз для прогину :

, (9.7)

де і сталі інтегрування.

Для обчислення інтегралів, що входять у формули (9.6) і (9.7), необхідно спочатку написати аналітичний вираз для згинального моменту. Сталі інтегрування знаходяться з граничних умов, що залежать від умов закріплення балки.

Розглянемо кілька прикладів застосування методу безпосереднього інтегрування наближеного диференціального рівняння пружної лінії балки.

Приклад 9.1. Визначити стрілу прогину і кут повороту перерізу В балки, зображеної на рис.9.3.

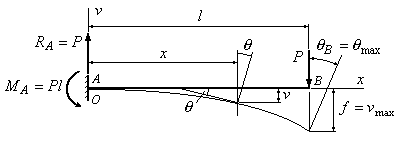
Рис.9.3

Розв’язок:

1. З умов рівноваги визначаємо опорні реакції:

; .

2. Вибираємо початок координат на лівому кінці балки, сполучаючи його з точкою А. Вісьспрямовуємо вгору, вісь вправо.

3. Складаємо рівняння згинального моменту в перерізі :

.

4. Припускаючи, що жорсткість балки є величиною сталою, записуємо наближене диференціальне рівняння пружної лінії балки:

.

Знак “+” у рівнянні пружної лиинии був прийнятий тому, що вісь спрямована вгору.

5. Інтегруємо рівняння перший раз. Одержимо:

(а)

Інтегруючи ще раз, одержуємо рівняння для прогину балки в перерізі :

(б)

Зважаючи не те, що в жорсткій опорі прогин і кут повороту дорівнюють нулю, для визначення сталих інтегрування граничні умови мають вигляд:

при ; при.

З рівняння (а) видно, що стала являє собою кут повороту на початку координат (переріз А). Задаючи в рівнянні (а), знаходимо. З рівняння (б) випливає, що стала прогин на початку координат. Задаючи в рівнянні (б) , одержуємо.

Таким чином, одержуємо наступні вирази для прогину і кута повороту:

,

.

Підставляючи в перше рівняння , знайдемо стрілу прогину:

.

Підставляючи в друге рівняння , знайдемо максимальний кут повороту:

.

Знак “” у прогину свідчить про те, що його напрямок не збігається з додатним напрямком осі . Знак “” у виразі для кута повороту показує, що переріз В повернувся не проти, а за годинниковою стрілкою.

Приклад 9.2. Визначити стрілу прогину двоопорної балки і кути повороту опорних перерізів А і В (Рис.9.4).

Розв’язок:

1. З умов рівноваги визначаємо опорні реакції:

.

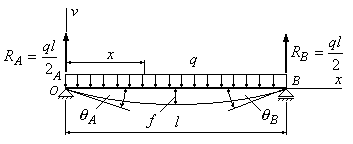
Рис.9.4

2. Вибираємо початок координат на лівому кінці балки, сполучаючи його з точкою А. Вісьспрямовуємо вгору, вісь вправо.

3. Складаємо рівняння для згинального моменту в перерізі :

.

4. Припускаючи, що жорсткість є сталою величиною, записуємо наближене диференціальне рівняння пружної лінії балки:

.

Знак “+” у рівнянні пружної лінії бул прийнятий тому, що вісь спрямована вгору.

5. Інтегруємо рівняння перший раз. Одержимо:

. (в)

Інтегруючи ще раз, одержуємо рівняння для прогину в перерізі :

. (г)

Сталі інтегрування знайдемо з граничних умов:

при ; при.

Підставляючи в рівняння (г) і дорівнюючи прогин нулю, одержимо; підставляючи в це ж рівняння, знаходимо сталу інтегрування:

.

Знайдені значення сталих інтегрування підставляємо у рівняння (в) і (г) і одержуємо рівняння для кутів повороту і прогинів:

;

.

Підставляючи тау перше рівняння одержимо кути повороту відповідно перерізів А і В:

; .

Завдяки симетрії навантаження максимальний прогин буде посередині балки. Підставляючи в друге рівняння , одержимо:

.

Як і в попередньому прикладі, знак “” у прогину свідчить про те, що його напрямок не збігається з додатним напрямком осі . Знак “” у виразі для кута повороту показує, що переріз А повернувся не проти, а за годинниковою стрілкою, знак “+” у виразі для кута поворотупоказує, що переріз В повернувся проти ходу годинникової стрілки.

Приклад 9.3. У скільки разів прогин у перерізі В на кінці зображеної на рис.9.5 балки, більший, ніж прогин у перерізі С посередині балки?

Розв’язання:

Скористаємося результатами, отриманими в прикладі 9.1. Запишемо остаточний вираз для прогину:

і підставимо в це рівняння координати точок С і В. Одержимо:

при ;

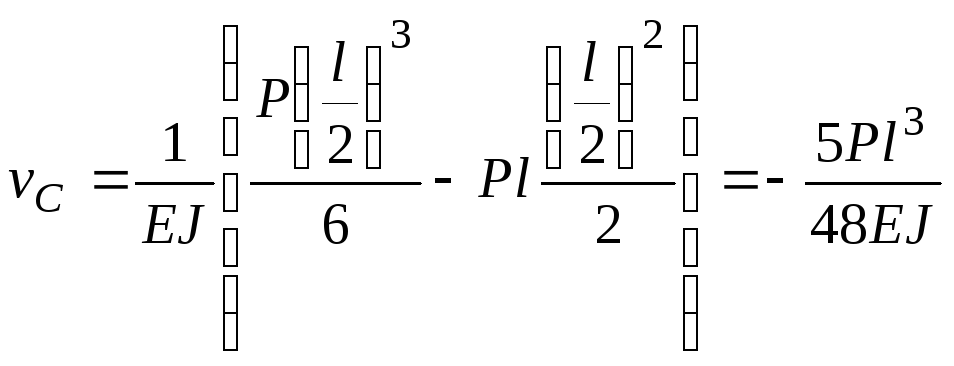при .

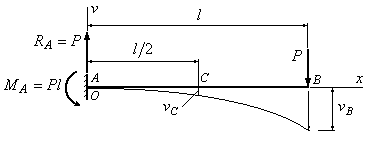
Рис.9.5

Порівнюючи отримані величини прогинів, дістаємо висновку, що прогин у перерізі В більший, ніж прогин у перерізі С в 3,2 рази:

.

Приклад 9.4. У скільки разів кут повороту перерізу А на кінці зображеної на рис.9.6 балки більший, ніж кут повороту перерізу В на відстані чверті прольоту від лівого кінця балки?

Рис.9.6

Розв’язок:

1. Знаходимо реакції: ; .

2. Вибираємо початок координат на правому кінці балки, сполучаючи його з точкою А. Вісьспрямовуємо вгору, вісь вліво.

3. Записуємо вираз для згинального моменту в перерізі :

.

4. Складаємо наближене диференціальне рівняння пружної лінії балки:

.

Знак “+” у рівнянні пружної лиинии був прийнятий тому, що вісь спрямована вгору.

5. Приймаємо жорсткість балки сталою. Інтегруємо диференціальне рівняння. Одержуємо:

. (д)

Сталу інтегрування в рівнянні (д) знайдемо з умови, що при кут повороту в перерізі А дорівнює нулю. Підставимо в рівняння (д)і дорівняємо нулю кут повороту перерізу А. Одержимо. Тоді остаточне рівняння для кута повороту набуває вигляду:

. (е)

6. Підставляємо у рівняння (е) координату , одержимо кут повороту в перерізі С:

.

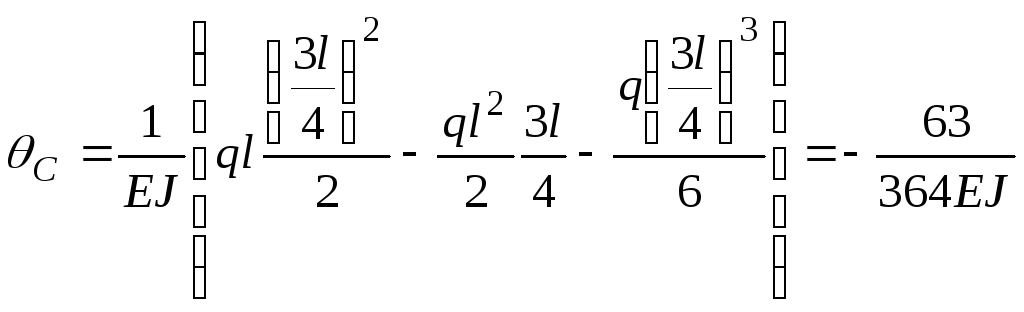7. Підставляємо у рівняння (е) координату . Одержимо кут повороту в перерізі В:

.

8. Порівнюючи кути повороту в перерізах В і С, одержимо:

Таким чином, кут повороту в перерізі В в 1,016 рази більший, ніж кут повороту в перерізі С.

Приклад 9.5. Знайти стрілу прогину (у мм) балки, зображеної на рис.9.7, якщо жорсткість поперечного перерізу балки дорівнює кНм².

Рис.9.7

Розв’язок:

Скористаємося розв’язком задачі, хід якого викладений у прикладі 9.4 і проінтегруємо вираз (д). Одержимо рівняння для прогину в перерізі :

. (ж)

Сталі інтегрування в рівнянні (ж) одержимо, скориставшись граничними умовами закріплення балки, відповідно до яких прогин і кут повороту у жорсткій опорі дорівнюють нулю:

при і.

Підставляючи в рівняння (д) і (ж) і дорівнюючи послідовно нулю кут повороту і прогин, одержимо:;. Тоді вираз для прогину набуває вигляду:

.

Підставляючи в це рівняння задані значення жорсткості перерізу, інтенсивності розподіленого навантаження, довжину балки, а також координату перерізу В, у якому визначається стріла прогину (), знаходимо:

ммм.

Знак “” у прогину свідчить про те, що його напрямок не збігається з додатним напрямком осі .