Задача 6.34.

Маємо гру гравців А і В, яка задана платіжною матрицею. Визначити ціну гри та оптимальні стратегії дій гравців А і В. Оптимізацію гри починають, як правило, визначенням домінуючих стратегій для кожної зі сторін, а також відкиданням невигідних і дублюючих стратегій.

За умови існування такої матриці розв’язок задачі — сідлову точку, ціну та оптимальні стратегії гри — можна знайти значно ефективніше:

Гравець A

Гравець В

Розв’язування. Насамперед визначають домінуючу стратегію. Перша стратегія гравця А домінує над третьою, оскільки всі значення його виграшів за будь-яких дій суперника є не гіршими, ніж у разі вибору третьої стратегії, тобто всі елементи першого рядка платіжної матриці не менші за відповідні елементи її третього рядка. Тому третя стратегія гірша за першу й може бути вилучена з платіжної матриці.

Аналізуючи далі можливі дії гравця B, зауважимо, що його перша стратегія домінує над четвертою, яку можна відкинути як більш збиткову, а тому невигідну для цього гравця. Отже, маємо таку платіжну матрицю:

.

У разі вибору гравцем А першої стратегії, залежно від дій гравця В він може отримати 6, 3, 8 або 9 одиниць. Але завжди його виграш буде не меншим за , тобто незалежно від поведінки гравця В. Якщо розглянути можливі наслідки вибору гравцем А другої стратегії, то аналогічно його гарантований виграш становитиме. Для третьої стратегії відповідно маємо:.

Отже, нижня ціна гри: , а гравець А для максимізації мінімального виграшу має обрати другу з трьох можливих стратегій. Така стратегія є максимінною в цій грі.

Гравець В, який намагається мінімізувати свій програш, обираючи першу стратегію, може програти 6,6 або 4 одиниці. Але за будь-яких варіантів дій гравця А він може програти не більш як . Для другої стратегії маємо, для третьої —, для четвертої —. Отже, верхня ціна гри.

І гравцю В доцільно вибирати другу стратегію, яка є мінімаксною у грі.

Оскільки , ця гра має сідлову точку, ціна гри дорівнює 5. Оптимальною максимінною стратегією гравця А є друга з трьох можливих стратегій його дій. Для гравця В оптимальною є також друга з чотирьох можливих.

6.5.2. Зведення матричної гри до задачі лінійного програмування

Якщо матрична гра не має сідлової точки, то знаходження її розв’язку, особливо за великої кількості стратегій, — доволі складна задача, яку можна ефективно розв’язати методами лінійного програмування.

Задача розглядається в такому формулюванні: знайти вектори ймовірностей із метою визначення оптимального значення ціни гри та оптимальних стратегій.

Зауважимо, що доведено основну теорему теорії ігор: кожна скінчена гра має принаймні один розв’язок, який можливий в області змішаних стратегій.

Отже, нехай маємо скінченну матричну гру з платіжною матрицею

.

Оскільки оптимальні стратегії гравців А і В дозволяють отримати виграш

,

то використання оптимальної змішаної стратегії гравцем А має забезпечувати виграш не менший за ціну гри в разі вибору гравцем В будь-яких стратегій. Математично ця умова записується так:

. (6.23)

Відповідно використання оптимальної змішаної стратегії гравцем В має за будь-яких стратегій гравця А забезпечувати програш В, що не перевищує ціни гри:

. (6.24)

Ці два співвідношення застосовують для знаходження розв’язку гри.

Отже, потрібно знайти , щоб

за умов

,

,

.

Зауважимо, що ціна гри невідома і має бути визначена під час розв’язування задачі.

Модель ігрової задачі може бути спрощена.

З (6.23) маємо:

Поділивши всі обмеження на , дістанемо:

Нехай , тоді

Згідно з умовою , звідки.

Отже, цільова функція початкової задачі набирає такого вигляду:

.

У результаті задача лінійного програмування:

(6.25)

за умов

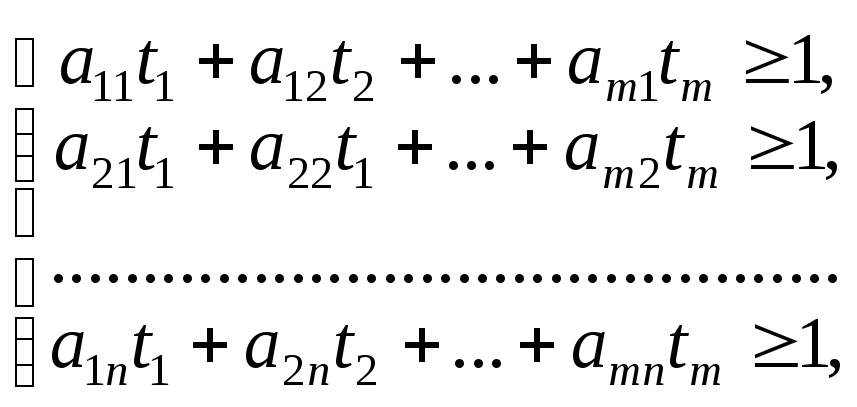(6.26)

. (6.27)

Розв’язавши цю задачу симплексним методом, знайдемо значення , а такожі, тобто визначимо змішану оптимальну стратегію для гравця А.

За аналогією запишемо задачу лінійного програмування для визначення оптимальної стратегії гравця В. Нехай

.

Тоді маємо таку лінійну модель:

за умов

.

Очевидно, що задача лінійного програмування для гравця В є двоїстою до задачі гравця А, а тому оптимальний розв’язок однієї з них визначає оптимальний розв’язок спряженої.

Розглянемо приклад на застосування методів лінійного програмування до знаходження оптимального розв’язку гри.