Задача 6.3.

Задача комівояжера. В економічному регіоні розміщено 6 пунктів (міст). Комівояжер, який виїжджає з міста 1, має побувати в кожному місті один раз і повернутися до вихідного пункту. Знайти найкоротший маршрут, якщо відстані між містами відомі (рис. 6.2).

Рис. 6.2

Записати загальну і числову економіко-математичну модель.

Розв’язування. Нехай маємоnпунктів, де має побувати комівояжер.

Позначимо:

Отже, х_ij — бульові (цілочислові) змінні. Цільовою функцією цієї задачі є мінімізація всього маршруту комівояжера:

де с_ij — відстань між містами і та j.

Обмеження щодо одноразового в’їзду в кожне місто:

.

Обмеження щодо одноразового виїзду з кожного міста:

.

Ці обмеження не повністю описують допустимі маршрути і не виключають можливості розриву маршруту. Щоб усунути цей недолік, введемо додаткові змінні u_i(u_j) , які набувають невід’ємних цілих значень. Запишемо обмеження, які виключають можливість існування підмаршрутів:

,

де u_i (u_j) — порядковий номер міста за маршрутом прямування комівояжера.

Запишемо числову економіко-математичну модель комівояжера за розглядуваних умов.

Критерій оптимальності:

;

а) обмеження щодо одноразового в’їзду в кожне місто:

,

,

,

,

,

;

б) обмеження щодо одноразового виїзду з кожного міста:

,

,

,

,

,

;

в) обмеження щодо виключення підмаршрутів:

,

,

,

,

,

,

,

,

,

,

,

,

,

;

,

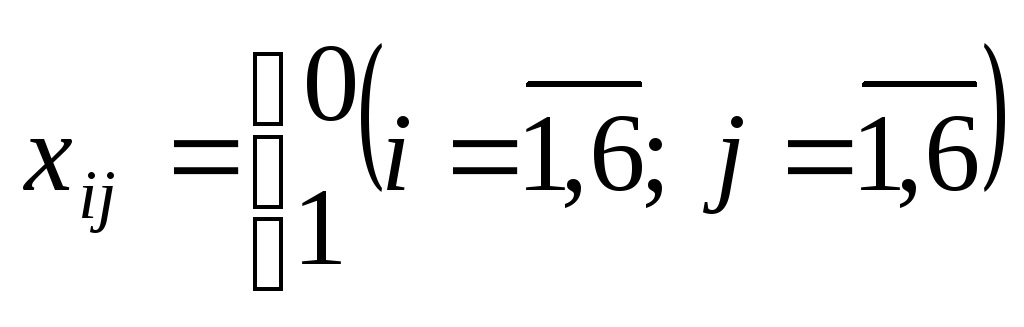u_i(u_j) — цілі числа .

Такі задачі розв’язуються спеціальними методами [1; 10].

Зауважимо, що аналогічні задачі нерідко постають на практиці, наприклад, у дрібному бізнесі.

Фірма у місті має 25 кіосків, які торгують безалкогольними напоями. Щоденно з бази автомобілем розвозять до них товар. Як оптимально організувати розвезення відповідної кількості товару?

Задача 6.4.

Фермер планує виробляти три види продукції — озиму пшеницю, цукрові буряки та молоко. Сумарні витрати складаються з двох частин: постійних — k_j, які не залежать від обсягу виробництва, і поточних c_j на виробництво одиниці продукції, де j — номер продукції. Відповідні дані наведено в таблиці:

Показник	Вид продукції
	Озима пшениця, т	Цукровий буряк, т	Молоко, т
Постійні витрати, тис. грн.	40	70	20
Поточні витрати на одиницю продукції, грн.	400	150	500
Норма витрат ріллі, га	0,2	0,02	0,25
Ціна одиниці продукції, грн.	800	300	1000

Визначити оптимальний план виробництва продукції кожного виду, якщо з цією метою використовується 100 га ріллі.

Розв’язування. Нехай x_j — обсяг виробництва j-го виду продукції, . Функція сумарних витрат на виробництвоj-ї продукції набуває вигляду:

Як цільову функцію беремо максимізацію валового прибутку:

де y_j — ціна одиниці j-ї продукції.

Обмеження щодо ріллі:

де а_j — норма витрат ріллі на одиницю j-ї продукції; А — ресурс ріллі.

Цільова функція цієї задачі не є лінійною, оскільки має розрив у початку координат. Отже, ця задача не може бути розв’язана симплексним методом.

Щоб розв’язати цю задачу, скористаємося штучним прийомом. Введемо бульові змінні такою умовою:

її можна записати у вигляді лінійної нерівності

,

де М — досить велике число, за якого умова виконується для всіх допустимих обсягів виробництва продукції.

У результаті маємо таку економіко-математичну модель:

за умов

,

,

, .

Запишемо числову економіко-математичну модель. Очевидно, що максимум пшениці становить 500 т, цукрових буряків — 5000 т, молока —400 т. Отже,М може дорівнювати 5000. Звідси маємо:

за умов

,

,

,

,

.

Пропонуємо розв’язати аналогічну задачу, оцінивши ефективність нового бізнесу.

Звичайно, у реальній ситуації існує більший набір можливих видів продукції, а також багато обмежень щодо ресурсів.