
- •Лабораторна робота № 5
- •Методичні вказівки щодо виконання завдання 5.1
- •Практичне завдання № 5.1 (для варіантів №№ 1-30)
- •Методичні вказівки щодо виконання завдання 5.2
- •Практичне завдання № 3.2 (для варіантів №№ 1-30)
- •Методичні вказівки щодо виконання завдання 5.3
- •Практичне завдання № 5.4 (для варіантів №№ 1-30)
Лабораторна робота № 5
Тема «Аналіз інтенсивності динаміки. Аналіз тенденцій розвитку та коливань»
Мета роботи: поглиблення теоретичних знань і набуття практичних навичок щодо застосування методів визначення показників інтенсивності динаміки, основної тенденції ряду динаміки, оцінки сезонних коливань та сталості динаміки, а також їх графічного зображення.
Час виконання роботи – 4 години
Методичні вказівки щодо виконання завдання 5.1
Для вивчення зміни соціально-економічних явищ у часі використовують систему абсолютних та відносних статистичних показників. Ця система включає дві групи характеристик:
1) показники інтенсивності зміни рівнів динамічного ряду:
абсолютний приріст;
темп зростання;
темп приросту;
абсолютне значення 1% приросту;
2) середні показники динамічного ряду:
середній рівень ряду;
середній абсолютний приріст;
середній темп зростання;
середній приріст.
Обчислення показників інтенсивності зміни рівнів ряду динаміки грунтується на абсолютному або відносному зіставленні між собою рівнів ряду динаміки.
Рівень, який зіставляється називається поточним, а рівень, яким зіставляють інші рівні –базисним. За базу зіставлення приймають або попередній, або початковий ( перший) рівень ряду динаміки.
Якщо кожний наступний рівень зіставляють з попереднім, то отримують ланцюгові показники динаміки, а якщо кожний наступний рівень зіставляють з рівнем, взятим за базу зіставлення, то одержані показникибазисні.
За постійну базу порівняння можна прийняти не лише початковий, а й будь – який інший рівень ряду: середній рівень будь-якого попереднього періоду, обгрунтований історично та економічно.
Абсолютний приріст(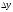 )
обчислюється як різниця між поточним
і базисним рівнями і показує на скільки
одиниць підвищився чи зменшився рівень
порівняно з базисним за певний проміжок
часу:
)
обчислюється як різниця між поточним
і базисним рівнями і показує на скільки
одиниць підвищився чи зменшився рівень
порівняно з базисним за певний проміжок
часу:
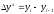 ‑ ланцюговий;
(5.1)
‑ ланцюговий;
(5.1)
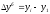 ‑ базисний;
(5.2)
‑ базисний;
(5.2)
де  абсолютний
приріст;
абсолютний
приріст;
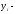 поточний
рівень ряду;
поточний
рівень ряду;
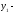 початковий
( перший) рівень ряду;
початковий
( перший) рівень ряду;
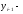 попередній
рівень ряду.
попередній
рівень ряду.
Абсолютний приріст виражається в тих же одиницях виміру, що й рівні ряду. Якщо абсолютна швидкість зміни рівнів ряду динаміки додатна, то маємо абсолютний приріст, а якщо від’ємна – абсолютне зменшення.
Темп зростапння Тзр.характеризує відносну швидкість зміни рівнів ряду динаміки й обчислюється як співвідношення зіставлюваного рівня з рівнем, прийнятим за базу порівняння і обчислюється за формулою:
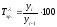 ‑ ланцюговий; (5.3)
‑ ланцюговий; (5.3)
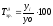 _ базисний. (5.4)
_ базисний. (5.4)
Темп зростання показує, у скільки разів змінився рівень часового ряду за певний проміжок часу.
Коефіцієнт зростання може виражатися у формі коефіцієнта і називатися коефіцієнтом зростання, та у формі відсотка і називатисятемпом зростання.
Темп приросту Тпр.визначаєтьсяяк відношення абсолютного приросту до абсолютного або початкового рівня і показує на скільки % порівнюваний рівень більший або менший від рівня, взятого за базу порівняння, тобто:
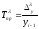 ‑ ланцюговий;
(5.5)
‑ ланцюговий;
(5.5)
 ‑базисний.
(5.6)
‑базисний.
(5.6)
Між темпами зростання та приросту існує безпосередній взаємозв’язок:
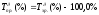 (5.7)
(5.7)
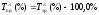 (5.8)
(5.8)
Абсолютне значення одного відсотка приросту (А%) визначається шляхом ділення абсолютного приросту на темп приросту за один і той же період часу. Абсолютне значення одного відсотка приросту вираховується технічно простішим способом – діленням початкового рівня на 100, оскільки за 100.0відсотків завжди приймається базисний рівень, а 1,0% буде в 100 разів менший від базисного рівня.
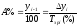 (5.9)
(5.9)
Оскільки при визначенні базисних
показників база порівняння є постійною,
то абсолютна величина 1% приросту
залишається теж незмінною
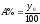 ,
і тому для базисних приростів абсолютне
значення одного відсотка приростуА%
не визначається.
,
і тому для базисних приростів абсолютне
значення одного відсотка приростуА%
не визначається.
Динамічні ряди складаються з багатьох варіаційних рівнів і тому потребують деяких узагальнюючих характеристик.Для цього обчислюють наступні середні показники:
середні рівні ряду;
середні абсолютні прирости;
середні темпи зростання;
середні темпи приросту.
Методи обчислення середнього рівня ряду залежать від їх виду.
В інтервальних рядах з рівними періодами середній рівень ряду обчислюють за формулою середньої арифметичної простої:
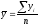 (5.10)
(5.10)
де
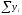 ‑ сума
рівнів ряду;
‑ сума
рівнів ряду;
n– число рівнів ряду.
Якщо окремі періоди інтервального часового ряду мають різну довжину, то для визначення середнього рівня використовують середню арифметичну зважену:
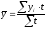 (5.11)
(5.11)
де
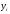 ‑
рівні ряду;
‑
рівні ряду;
 – проміжки
часу.
– проміжки
часу.
В моментних рядах з рівними або приблизно рівними проміжками часу між сусідніми датами середній рівень визначають за формулою середньої хронологічної простої:
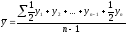 (5.12)
(5.12)
де
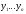 ‑
рівні ряду;
‑
рівні ряду;
n– число рівнів ряду.
Інакше обчислюють середні рівні в момент них рядах з нерівними інтервалами – за допомогою середньої хронологічної зваженої:
 ,
(5.13)
,
(5.13)
де
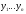 ‑ рівні
ряду;
‑ рівні
ряду;
n ‑ тривалість терміну часу між рівнями.
Середній абсолютний приріст(середня абсолютна швидкість) визначається як середня арифметична проста з ланцюгових абсолютних приростів за певні періоди і показує на скільки одиниць у середньому змінився рівень порівняно з попереднім.
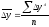 ,
(5.14)
,
(5.14)
 ‑ середній
абсолютний приріст;
‑ середній
абсолютний приріст;
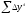 ‑ сума
ланцюгових приростів;
‑ сума
ланцюгових приростів;
n ‑ кількість приростів.
Оскільки сума ланцюгових приростів
( )
дорівнює приросту за весь період, то
формула середнього абсолютного приросту
має вигляд:
)
дорівнює приросту за весь період, то
формула середнього абсолютного приросту
має вигляд:
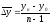 (5.15)
(5.15)
Кількість абсолютних приростів менша від кількості рівнів динамічного ряду на одиницю.
Середній абсолютний приріст ряду динаміки показує, на скільки в середньому на одиницю часу (щорічно, щомісячно тощо) у досліджуваному періоді змінювались рівні ряду.
Середній темп зростання характеризує інтенсивність зміни рівнів ряду динаміки та показує, у скільки разів в середньому за одиницю часу змінився рівень ряду й зводиться до визначення за формулою:
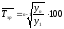
 (5.16)
(5.16)
де 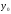 ‑ початковий
рівень ряду;
‑ початковий
рівень ряду;
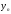 ‑кінцевий
рівень ряду;
‑кінцевий
рівень ряду;
 ‑кількість
півнів динамічного ряду
‑кількість
півнів динамічного ряду
Середній темп зростання визначається за формулою середньої геометричної із ланцюгових коефіцієнтів росту:
 (5.17)
(5.17)
де
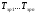 ‑ ланцюгові
темпи (коефіцієнти) зростання;
‑ ланцюгові
темпи (коефіцієнти) зростання;
 ‑число
змінних темпів зростання;
‑число
змінних темпів зростання;
Середній темп зростання обчислюють, окрім середньої геометричної простої, ще й за формулою середньої геометричної зваженої:
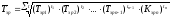 (5.18)
(5.18)
де
 термін
часу, протягом якого зберігається темп
зростання;
термін
часу, протягом якого зберігається темп
зростання;
 –сума
всіх відрізків часу.
–сума
всіх відрізків часу.
Середній темп приросту не може бути визначений безпосередньо на основі послідовних темпів приросту або показників середнього абсолютного приросту.
Його визначають як різницю між середнім темпом зростання і 100:
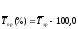 (5.19)
(5.19)
Середній темп приросту вказує на те, на скільки відсотків збільшився або зменшився рівень ряду порівняно з попереднім у середньому за одиницю часу.
