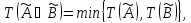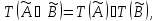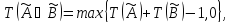Потім знаходять вислідні функції належності кожного правила:

(5.11)

3. Нечітка композиція (aggregation). Знаходять вислідну функцію належності всієї сукупності правил при вхідних сигналах та :

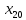(5.12)

4. Зведення до чіткості (defuzzification). Використовують, коли потрібно перетворити вихідну функцію належності у конкретне значення . Найбільш поширений центроїдний метод.

Якщо в наведеному алгоритмі логічна операція перетину реалізується як функція «мінімум», а об’єднання – як «максимум», то це алгоритм Мамдані (або Мамдані-Заде).

На практиці широко застосовують алгоритм нечіткого логічного висновку Сугено (Sugeno), відомий також як алгоритм Такагі-Сугено-Канга (TSK). Відмінною рисою даного алгоритму є простота обчислень.

Проджувальні правила в алгоритмі Сугено мають такий вигляд:

(5.13)

де – звичайна чітка функція;

r – номер правила.

Принципова відмінність від алгоритму Мамдані полягає в тому, що висновок подають у формі функціональної залежності.

Реалізація алгоритму Сугено складається із трьох кроків:

1. Введення. Цілком аналогічне алгоритмові Мамдані.

2. Нечітка імплікація. Знаходять функції належності передумов кожного окремого правила за конкретних вхідних сигналів :

(5.14)

де – кількість породжувальних правил. У класичному алгоритмі Сугено логічна операція перетину реалізується як min.

3. Зведення до чіткості (defuzzification). Визначається чітке значення вихідної змінної:

(5.15)

Як функцію 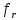часто використовують поліноми нульового порядку:

(5.15)

або першого порядку:

(5.16)

де та – деякі сталі.

В залежності від типу функції 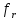дані алгоритми називають алгоритмами Сугено нульового або першого порядку відповідно.

Формально алгоритм Ларсена може бути визначений наступними кроками:

1. формування бази правил систем нечіткого виводу;

2. фазифікації вхідних змінних;

3. агрегація підумови в нечітких правилах продукцій. Використовуються парні нечіткі логічні операції для знаходження ступеня істинності умов всіх правил нечітких продукцій (як правило, max-диз’юнкція і min-кон’юнкція). Ті правила, ступінь істинності умов яких відмінна від нуля, вважаються активними і використовуються для подальших розрахунків;

4. активізація підзаключень в нечітких правилах продукцій. Здійснюється використуванням формули:

(5.17)

за допомогою чого знаходиться сукупність нечітких множин: С = {с₁, с₂ , ..., с_q}, де q – загальна кількість підзаключень в базі правил;

5. акумуляція висновків нечітких правил продукцій. Здійснюється за формулою:

(5.18)

для об’єднання нечітких множин, відповідних термам підзаключень, що відносяться до одних і тих же вихідних лінгвістичних змінних;

6. дефазифікація вихідних змінних. Може використовуватися будь-який з методів дефазифікації.

Завдання полягає в тому, щоб розробити прототип експертної системи, яка була б реалізована у вигляді системи нечіткого висновку і дозволяла б визначити максимальну ефективність від вкладу депозиту в сумі 50 000 грн. між чотирма різними банками, на основі суб’єктивних оцінок трьох експертів.

Емпіричні знання в даній проблемній області можуть бути представлені у формі наступних евристичних продукційних правил.

Таблиця 5.1 – Перелік евристичних продукційних правил

№	Вхідні значення				Вихідне значення
	Відсоткова ставка	Рівень довіри	Додаткові можливості	Ефективність від вкладу в депозит
1	Низька	Низький	Малі	Низька
2	Низька	Низький	Середні	Низька
3	Низька	Низький	Великі	Низька
4	Низька	Середній	Малі	Низька
5	Низька	Середній	Середні	Середня
6	Низька	Середній	Великі	Середня
7	Низька	Високий	Малі	Середня
8	Низька	Високий	Середні	Середня
9	Низька	Високий	Великі	Середня
10	Середня	Низький	Малі	Низька
11	Середня	Низький	Середні	Середня
12	Середня	Низький	Великі	Середня
13	Середня	Середній	Малі	Середня
14	Середня	Середній	Середні	Середня
15	Середня	Середній	Великі	Середня
16	Середня	Високий	Малі	Середня
17	Середня	Високий	Середні	Середня
18	Середня	Високий	Великі	Велика

Продовження таблиці 5.1

№	Вхідні значення				Вихідне значення
	Відсоткова ставка	Рівень довіри	Додаткові можливості	Ефективність від вкладу в депозит
19	Висока	Низький	Малі	Низька
20	Висока	Низький	Середні	Середня
21	Висока	Низький	Великі	Середня
22	Висока	Середній	Малі	Середня
23	Висока	Середній	Середні	Середня
24	Висока	Середній	Великі	Велика
25	Висока	Високий	Малі	Велика
26	Висока	Високий	Середні	Велика
27	Висока	Високий	Великі	Велика

Дана інформація буде використана при побудові бази правил системи нечіткого висновку, яка дозволить реалізувати дану модель нечіткого управління.

Перейдемо до першого етапу процесу нечіткого виведення – «Формування бази нечітких лінгвістичних правил». Процес формування бази правил нечіткого виводу є формальне подання емпіричних знань експерта в тій чи іншій проблемній області.

В першу чергу варто для всіх змінних визначити відповідні лінгвістичні змінні. В нашому випадку таких лінгвістичних змінних три – це відсоткова ставка, рівень довіри і додаткові можливості.

Для оцінки першої з вхідних змінних експертами була складена таблиця рівнів відсоткової ставки, відповідно до якої група експертів її оцінювала.

Таблиця 5.2 – Рівні відсоткової ставки

№	Рівень	Критерій	Шкала від 0 до 50
1	Низький	Депозит не є ефективним, процент покриває знецінення інфляцією та приносить досить малий дохід	0-20

Продовження таблицы 5.2

№	Рівень	Критерій	Шкала від 0 до 50
2	Средній	Депозит в цілому є ефективним, процент покриває знецінення інфляцією та при носить значний дохід	20-34
3	Високий	Депозит є дуже ефективним, проценти приносять значні прибутки	35-50

Таблиця 5.3 – Рівні довіри до банку

№	Рівень	Критерій	Шкала від 0 до 50
1	Низький	Банк не є популярним, спостерігається відтік клієнтів, можливе збанкрутування	0-20
2	Средній	Населення вцілому банку довіряє, банк має хороші фінансові показники та перспективи розвитку	21-40
3	Високий	Великий банк, що давно завоював довіру клієнтів на ринку, має великий капітал, хорошу репутацію та добре налагоджену розгалуджену систему обслуговування клієнтів	41-50

Таблиця 5.4 – Додаткові можливості

№	Рівень	Критерій	Шкала від 0 до 10
1	Малі	Банк надає обмежені послуги, має вузьку систему банкоматів та відділень	0-3
2	Средні	Банк має розгалужену систему філій, відділень, банкоматів, надає можливості переказу коштів через інтернет-системи, гнучкі системи кредитування тощо	5-7
3	Великі	Можливості інтерне-банкінгу, прямі зв’язки з іноземними банками, надання послуг з використанням новітніх технологій (нові типи карток, програми під мобільні пристрої) тощо	8-10

Таблиця 5.5 – Ефективність від вкладу

№	Рівень	Шкала від 0 до 1
1	Низька	0-0,4
2	Середня	0,5-0,7
3	Велика	0,8-1

Слід зазначити, що вхідні та вихідні лінгвістичні змінні вважаються визначеними, якщо для них задані функції приналежності.

В таблице 5.6 задані критеріальні експертні оцінки ефективності від вкладу депозиту в чотирьох банках:

Таблиця 5.6 – Критеріальні експертні оцінки ефективності від вкладу депозиту в чотирьох банках

Експерт			Критерій
D1	C1	0,654	25	23	21	12
D2	C2	0,265	55	22	14	54
	C3	0,256	2	8	9	15
	C1	0,145	55	66	21	75
D3	C2	0,125	33	65	78	52
	C3	0,145	5	1	5	6
	C1	0,255	25	66	54	21
Експерт	C2	0,355	26	52	54	22
	C3	0,588	1	6	7	4
	Критерій	Вага	P1	P2	P3	P4

Для одержання узагальнених оцінок проекту від кожного експерта, критеріальні оцінки кожного експерта агрегуємо за допомогою системи НЛВ із зваженою істинністю. Система НЛВ має 3 входи, що відповідають критеріям оцінювання та одне вихідне значення – ефективності від вкладу депозиту.

Лінгвістичні змінні, що відповідають вхідним значенням, мають по три значення:

1. рівень відсоткової ставки = {низький, середній, високий};

2. рівень довіри до банку = {низький, середній, високий};

3. додаткові можливості = {малі, середні, великі};

Лінгвістична змінна виходу системи НЛВ також має три градації: ефективність від вкладу = {низька, середня, велика}.

Для відповідних нечітких множин входу та виходу застосовуються трикутні функції належності.

База правил системи НЛВ наведена в таблиці 5.7.

Таблиця 5.7 – База правил системи нечіткого логічного висновку

№	Правила нечіткого логічного висновку
	Вхідні значення				Вихідне значення
	Відсоткова ставка	Рівень довіри	Додаткові можливості	Ефективність від вкладу в депозит
1	Низька	Низький	Малі	Низька
2	Низька	Низький	Середні	Низька
3	Низька	Низький	Великі	Низька
4	Низька	Середній	Малі	Низька
5	Низька	Середній	Середні	Середня
6	Низька	Середній	Великі	Середня
7	Низька	Високий	Малі	Середня
8	Низька	Високий	Середні	Середня
9	Низька	Високий	Великі	Середня
10	Середня	Низький	Малі	Низька
11	Середня	Низький	Середні	Середня
12	Середня	Низький	Великі	Середня
13	Середня	Середній	Малі	Середня
14	Середня	Середній	Середні	Середня
15	Середня	Середній	Великі	Середня
16	Середня	Високий	Малі	Середня
17	Середня	Високий	Середні	Середня
18	Середня	Високий	Великі	Велика
19	Висока	Низький	Малі	Низька

Продовження таблиці 5.7

№	Правила нечіткого логічного висновку
	Вхідні значення			Вихідне значення
	Відсоткова ставка	Рівень довіри	Додаткові можливості	Ефективність від вкладу в депозит
20	Висока	Низький	Середні	Середня
21	Висока	Низький	Великі	Середня
22	Висока	Середній	Малі	Середня
23	Висока	Середній	Середні	Середня
24	Висока	Середній	Великі	Велика
25	Висока	Високий	Малі	Велика
26	Висока	Високий	Середні	Велика
27	Висока	Високий	Великі	Велика

Фазифікацією, або введенням нечіткості, називається процес знаходження функції приналежності нечітких множин на основі звичайних вихідних даних. На даному етапі встановлюється відповідність між чисельним значенням вхідної змінної системи нечіткого виводу і значенням функції приналежності відповідної їй лінгвістичної змінної.

Після завершення цього етапу для всіх вхідних змінних повинні бути визначені конкретні значення функцій приналежності по кожному з лінгвістичних термів, які використовуються в підумові бази правил системи нечіткого виводу.

Результат фазифікації вхідних змінних представлено на рисунках 5.3 - 5.5.

Рисунок 5.3 – Фазифікація вхідної змінної «Рівень відсоткової ставки»

142

143

Рисунок 5.4 – Фазифікація вхідної змінної «Рівень довіри»

144

Рисунок 5.5 – Фазифікація вхідної змінної «Додаткові можливості»

Наступним кроком буде проведення етапу агрегації. Агрегація являє собою процедуру визначення ступеня істинності умов по кожному з правил системи нечіткого виводу.

Формально процедура агрегування виконується наступним чином. До початку цього етапу передбачаються відомими значення істинності всіх підумов системи нечіткого висновку, тобто множина значень В = {b_i'}. Далі розглядається кожне з умов правил системи нечіткого виводу. Якщо умова правила є нечітке висловлювання, то ступінь його істинності дорівнює відповідному значенню b_i'.

Якщо ж умова складається з декількох підумов, причому лінгвістичні змінні в підумові попарно не дорівнюють один одному, то визначається ступінь істинності складного висловлювання на основі відомих значень істинності підумови. При цьому для визначення результату нечіткої кон'юнкції або зв'язки "І" може бути використано одну з формул:

	(5.19)
	(5.20)
	(5.21)

а для визначення результату нечіткої диз'юнкції або зв'язки "АБО" може бути використана одна з формул:

	(5.22)
	(5.23)
	(5.24)

При цьому значення b_i' використовуються в якості аргументів відповідних логічних операцій. Тим самим знаходяться кількісні значення істинності всіх умов правил системи нечіткого виводу. Етап агрегування вважається закінченим, коли будуть знайдені всі значення b_i'' для кожного з правил R_k, що входять у розглянуту базу правил Р системи нечіткого виводу. Цю множину значень позначимо через В"= {b₁'', b₂'', ..., b_n''}

Оскільки в нас нечітка кон'юнкція або зв'язки "І", то скористаємось формулою 5.19 для проведення агрегації:

№	Відсоткова ставка	Рівень довіри	Додаткові можливості
1	0,00	0,00	0,50
2	0,00	0,00	0,00
3	0,00	0,00	0,00
4	0,00	0,00	0,50
5	0,00	0,00	0,00
6	0,00	0,00	0,00
7	0,00	0,00	0,50
8	0,00	0,00	0,00
9	0,00	0,00	0,00
10	1,00	0,00	0,50
11	1,00	0,00	0,00
12	1,00	0,00	0,00
13	1,00	0,00	0,50
14	1,00	0,00	0,00
15	1,00	0,00	0,00
16	1,00	0,00	0,50
17	1,00	0,00	0,00
18	1,00	0,00	0,00
19	0,00	0,00	0,50
20	0,00	0,00	0,00
21	0,00	0,00	0,00
22	0,00	0,00	0,50
23	0,00	0,00	0,00
24	0,00	0,00	0,00
25	0,00	0,00	0,50
26	0,00	0,00	0,00
27	0,00	0,00	0,00

Рисунок 5.6 – Результат проведення агрегації для першого експерта по першому банку

Аналогічно проводиться агрегація для решти експертів та банків загалом 12 разів (3 експерта на 4 банки).

Наступним етапом є активізація. Активізація в системах нечіткого виведення являє собою процедуру або процес знаходження ступеня істинності кожного з підвисновків правил нечітких продукцій. Активізація в загальному випадку багато в чому аналогічна композиції нечітких відносин, але не тотожна їй. Оскільки в системах нечіткого виведення використовуються лінгвістичні змінні, то формули для нечіткої композиції втрачають своє значення. В дійсності при формуванні бази правил системи нечіткого виводу задаються вагові коефіцієнти F_i для кожного правила (за умовчанням передбачається, якщо ваговий коефіцієнт не заданий явно, то його значення дорівнює 1).

Формально процедура активізації виконується наступним чином. До початку цього етапу передбачаються відомими значення істинності всіх умов системи нечіткого виведення, тобто множина значень В"= {b_i''} і значення вагових коефіцієнтів F_i для кожного правила. Далі розглядається кожне з висновків правил системи нечіткого вивода. Якщо висновок правила є нечітке висловлювання, то ступінь його істинності дорівнює алгебраїчному добутку відповідного значення b_i'' на ваговий коефіцієнт F_i. Якщо ж висновок складається з декількох під висновків, причому лінгвістичні змінні в підвисновках попарно не дорівнюють один одному, то ступінь істинності кожного з підвисновків дорівнює алгебраїчному добутку відповідного значення bi'' на ваговий коефіцієнт F_i. Таким чином, знаходяться всі значення с_k ступенів істинності підвисновків для кожного з правил R_k, що входять у розглянуту базу правил Р системи нечіткого виводу. Дану множину значень позначимо через С = {с₁, с₂ , ..., с_q}, де q-загальна кількість підвисновків в базі правил.

Після знаходження множини С = {с₁, с₂ , ..., с_q}, визначаються функції належності кожного з підвисновків для розглянутих вихідних лінгвістичних змінних. Для цієї мети можна методом нечіткої композиції «min-активація»:

(5.25)

де µ(х) – функція приналежності терма, який є значенням деякої вихідний змінної w_j, заданої на універсумі Y.

Етап активізації вважається закінченим, коли для кожної з вихідних лінгвістичних змінних, що входять в окремі підвисновки правил нечітких продукцій, будуть визначені функції приналежності нечітких множин їх значень, тобто сукупність нечітких множин: С₁, С₂, .. ., С_q, де q-загальна кількість підвисновків в базі правил системи нечіткого виводу.

В нашому випадку ступінь виконання кожного правила визначається за формулою:

(5.26)

Процедура імплікації за Мамдані:

(5.27)

Результат проведення активізиції для першого експерта по першому банку представлено на рисунку 5.7.

Рисунок 5.7 – Результат проведення активізації для першого експерта по першому банку

Наступним етапом є акумуляція. Акумулювання в системах нечіткого виведення являє собою процедуру або процес знаходження функції приналежності для кожної з вихідних лінгвістичних змінних множини W = {w₁, w₂, ..., w_s}.

Мета акумуляції полягає в тому, щоб об'єднати або акумулювати всі степені істинності висновків (підвисновків) для отримання функції приналежності кожної з вихідних змінних. Причина необхідності виконання цього етапу полягає в тому, що підвисновки пов'язані з однією і тією ж вихідною лінгвістичною змінною, належать різним правилам системи нечіткого виводу.

Формально процедура акумуляції виконується наступним чином. До початку даного етапу передбачаються відомими значення істинності всіх підвисновків для кожного з правил R_k, що входять у розглянуту базу правил Р системи нечіткого виводу, у формі сукупності нечітких множин: С₁, С₂ ,..., С_q, де q - загальна кількість підвисновків в базі правил. Далі послідовно розглядається кожна з вихідних лінгвістичних змінних w_j 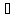W і пов'язані з нею нечіткі множини: C_j1, C_j2 ,..., C_jq. Результат акумуляції для вихідної лінгвістичної змінної w_j визначається як об'єднання нечітких множин C_j1, C_j2 ,..., C_jq за однією з формул.

Етап акумуляції вважається закінченим, коли для кожної з вихідних лінгвістичних змінних будуть визначені функції приналежності нечітких множин їх значень, тобто сукупність нечітких множин: С₁', С₂', ..., С_s' де s – загальна кількість вихідних лінгвістичних змінних в базі правил системи нечіткого вивода.

В нашому випадку акумуляція буде проводитись методом max-об'єднання нечітких множин за формулою:

(5.28)

Результат проведення акумуляції для першого експерта по першому банку представлено на рисунку 5.8.

Рисунок 5.8 – Результат проведення акумуляції для першого експерта по першому банку

Дефазифікація в системах нечіткого виведення являє собою процедуру або процес знаходження звичайного (не нечіткого) значення для кожної з вихідних лінгвістичних змінних множини W = {w₁, w₂, ..., w_s}.

Мета дефазифікації полягає в тому, щоб, використовуючи результати акумуляції всіх вихідних лінгвістичних змінних, отримати звичайне кількісне значення (Crisp value) кожної з вихідних змінних, яке може бути використане спеціальними пристроями, зовнішніми по відношенню до системи нечіткого виводу.

Тому дефазифікацію називають також приведенням до чіткості.

Формально процедура дефазифікації виконується наступним чином. До початку цього етапу передбачаються відомими функції приналежності всіх вихідних лінгвістичних змінних у формі нечітких множин: C₁', C₂',..., C_s', де s - загальна кількість вихідних лінгвістичних змінних в базі правил системи нечіткого виводу.

Далі послідовно розглядається кожна з вихідних лінгвістичних змінних w_j  W до якої відноситься нечітка множина Сj'. Результат дефазифікації для вихідний лінгвістічноъ змінної wj, визначається у вигляді кількісного значення y_i  R, отриманого за однією з розглянутих нижче формул.

Етап дефазифікації вважається закінченим, коли для кожної з вихідних лінгвістичних змінних будуть визначені кількісні значення у формі деякого дійсного числа, тобто у вигляді у₁, у₂ ,..., y_s, де s - загальна кількість вихідних лінгвістичних змінних в базі правил системи нечіткого виводу.

Для виконання чисельних розрахунків на етапі дефазифікації було використано метод дефазифікації центру ваги.

Центр ваги (CoG, COG, Centre of Gravity) або центроїд площі розраховується за формулою:

(5.29)

де у – результат дефазифікації;

х - змінна, відповідна вихідний лінгвістичній змінній w;

µ(х) – функція приналежності нечіткої множини, відповідної вихідної змінної w після етапу акумуляції.

Min і Мaх - ліва і права точки інтервалу носія нечіткої множини аналізованої вихідної змінної w.

При дефазифікації методом центру тяжіння звичайне (не нечітке) значення вихідної змінної дорівнює абсцисі центру ваги площі, обмеженою графіком кривої функції належності відповідної вихідної змінної.

Значення агрегованих за допомогою системи НЛВ оцінок всіх експертів для всіх проектів наведені в таблиці 5.7.

Таблиця 5.7 – Агреговані за допомогою системи НЛВ експертні оцінки ефективності від вкладу депозиту в чотирьох банках

Експерт	Досвідченість	P1	P2	P3	P4
D1	0,95	0,00	0,17	0,44	0,00
D2	0,87	0,00	0,00	0,00	0,00
D3	0,89	0,50	0,00	0,00	0,17

Тепер для подальшого розв’язку задачі знайдемо остаточну узагальнену оцінку кожного проекту – ефективність від вкладення в депозит. Рівень експертів неоднаковий, що виражається досвідченістю (табл. 5.7).

Розрахуємо ступені привабливості як середні значення агрегованих експертних оцінок проектів за формулою:

(5.30)

Результати наведені в таблиці 5.8.

Таблиця 5.8 – Остаточні оцінки ефективності від вкладу депозиту в чотирьох банках

	P1	P2	P3	P4
Розраховане значення	0,16	0,06	0,15	0,05
Нормоване значення	0,38	0,14	0,36	0,13

Відповідно до знайдених нормованих значень ступенів ефективності від вкладу депозиту в чотирьох банках з таблиці 5.8 на пропорційній основі визначимо значення інвестування кожного проекту виходячи з наявного бюджету, що складає 42 тис. грн. (таблиці 5.9)

Таблиця 5.9 – Значення обсягів вкладення

	Банки
	P1	P2	P3	P4
Розмір вкладів	15978,91	5685,38	15009,40	5326,30

Висновки: використання методу нечітких множин дає ряд переваг, тому що дозволяє:

• включати в аналіз якісні змінні;

• оперувати нечіткими вхідними даними;

• швидко моделювати складні динамічні системи і порівнювати їх із заданим ступенем точності;

• долати недоліки і обмеження існуючих методів оцінки проектних ризиків.

Недоліками методу є:

• суб’єктивність у виборі функцій приналежності і формуванні правил нечіткого введення;

• відсутність інформованості про метод, а також незначно увагу до застосування методу професійними фінансовими установами;

• необхідність спеціального програмного забезпечення, а також фахівців, які вміють з ним працювати.

Незважаючи на недоліки та обмеження теорії, метод нечітких множин отримав визнання як перспективного і дає точні результати рядом найбільших міжнародних компаній (Motorola, General Electric, Otis Elevator, Pacific Gas & Electric, Ford). Аналіз ризиків на основі статистичних методів для більшої частини нещодавно створених компаній не застосовується, тому що немає накопиченої статистичної інформації для отримання об’єктивних оцінок. Таким чином, метод нечітких множин не виключає застосування статистичних методів, а стає інструментом, коли інші підходи використати неможливо.